LEZIONI_2

Principi fisici di conversione
avanzata (Energetica L.S.)
G.Mazzitelli
ENEA
Seconda Lezione
Seconda Lezione
•
•
•
•
•
•
•
•
•
•
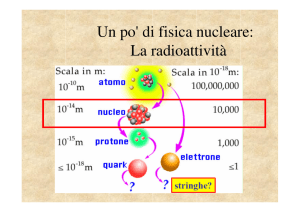
I costituenti nucleari
Le dimensione e la forma dei nuclei
Le masse nucleari e le energie di legame
La forza nucleare
Il decadimento radioattivo
Leggi di conservazione nel decadimento radioattivo
Il decadimento alfa
Il decadimento beta
Il decadimento gamma
La radioattività naturale
Forze fondamentali
• Forza gravitazionale (Moto dei corpi celesti,
meccanica newtoniana)
• Forza elettromagnetica (Equazioni di
Maxwell)
• Forza nucleare o forte
Radioattività
• La scoperta nel 1896 da parte di Henri
Becqurel della radioattività dell’uranio è
all’origine della fisica nucleare.
• Certi nuclei (NON TUTTI!!) si trasformano
spontaneamente da un valore di Z e N ad
un altro
• Generalmente per ogni valore di A vi sono
uno o più nuclei stabili
Radioattività
• Nei nuclei leggeri il numero dei protoni e
quello dei neutroni sono circa uguali
• Nei nuclei più pesanti N>Z Per bilanciare la
maggiore repulsione coulombiana è
necessario un maggior numero di neutroni.
• Non ci sono nuclei stabili con A=5 o A=8
Radioattività
Nuclei stabili
Radioattività
• I nuclei instabili si trasformano in altre
specie nucleari attraverso due processi che
cambiano Z e N di un nucleo:
– Decadimento alfa
– Decadimento beta
• Stati eccitati dei nuclei possono emettere
dei fotoni senza cambiamento di Z e N :
– Decadimento gamma
Radioattività
• Il numero di decadimenti al secondo
definisce l’attività di un materiale. L’attività
è indipendente dal tipo di decadimento o
dall’energia della radiazione emessa.
• L’unita di misura dell’attività è il curie
1 curie =3.7 10 10 decadimenti/secondo
1 Bq = 1 decadimento/secondo
Radioattività
Indichiamo con λ la probabilità di un decadimento / nucleo·secondo
L’attività A dipende dal numero di atomi radioattivi N e dalla
probabilità di decadimento
A  N
λ=cost
D’altra parte A è anche la variazione nel tempo del nuclei
radioattivi
dN
A 
dt
Radioattività
Pertanto abbiamo
dN
  N
dt

N  N oe
 t
1
Dove N0 è il numero di nuclei radiottivi al tempo t=0.
L’eq.(1) è
la legge esponenziale del decadimento
radioattivo da cui possiamo dedurre come il numero di
nuclei radioattivi decade in un campione.
Radioattività
In effetti non misuriamo N ma l’attività A che otteniamo
dall’eq.(1) moltiplicando per λ
A  Aoe
 t
(2)
Dove A 0 è l’attività al tempo t=0 .L’eq.(2)in funzione del tempo in
un grafico semilogaritmico ha il seguente andamento:
Da cui si ricava λ
Radioattività
• Il tempo di dimezzamento (half life) è il tempo necessario
a diminuire l’attività di un fattore 2, cioè:
A0
  t1 / 2
 A0e
2
Da cui:
t1/ 2 
1

ln 2 
È il tempo di vita medio è

1

0.693

Esempio
Il tempo di dimezzamento del 198Au è 2.70 giorni.
• Quale è la costante di decadimento del 198Au ?
• Quale è la probabilità che un 198Au decade in un
secondo ?
• Se avessimo un microgrammo di 198Au, quale è la
sua attività ?
• Quanti decadimenti avvengono se il campione e
vecchio di una settimana ?
Esempio
a)
0.693
0.693
 6 1


 2.97x10 s
t1/ 2
2.7x24x3600
b)
La probabilità di decadimento per secondo è
proprio la costante di decadimento, così che la
probabilità di decadimento per 198Au è
2.97x10-6
Esempio
c) Il numero di atomi nel nostro campione è determinato
dal numero di Avogrado e dalla massa di una mole
6
23
mN A 10 g x 6.02x10 atomi / mole
N

M
198g / mole
 3.04x1015 atomi
A  N  (2.97 10 6 s 1x3.04 1015 )
 9.03 10 deca dim enti / sec ondo
9
 0.244 Ci
Esempio
c) Il numero di atomi nel nostro campione è determinato
dal numero di Avogrado e dalla massa di una mole
6
23
mN A 10 g x 6.02x10 atomi / mole
N

M
198g / mole
 3.04x1015 atomi
A  N  (2.97 10 6 s 1x3.04 1015 )
 9.03 10 deca dim enti / sec ondo
9
 0.244 Ci
Esempio
d)
L’attività di decadimento è:
A  Aoe
t
 9.03 10 e
9
 ( 0.693/ 2.7 g )( 7 g )
 1.50 10 deca dim enti / sec ondo
9
Radioattività
• Nel processo di decadimento si conservano le
seguenti quantità:
–
–
–
–
–
Energia
Impulso
Momento angolare
Carica elettrica
Numero di massa
Radioattività – Leggi di conservazione
Conservazione dell’Energia
Un nucleo X decadrà in un nucleo più leggero X* con
l’emissione di una o più particelle che indicheremo con x
ovverosia:
X
X* + x
soltanto se l’energia a riposo di X è più grande dell’energia
a riposo totale di X* + x. L’eccesso di energia e definito
come il Q del decadimento:
Q  m N  X   m N X *   m N  x c 2  0
dove mN è la massa nucleare
Radioattività – Leggi di conservazione
Conservazione dell’impulso
se il nucleo che decade era inizialmente a riposo poi
la somma totale dell’impulso di tutti i prodotti di
decadimento deve essere zero
pX*  px  0
Radioattività – Leggi di conservazione
Conservazione del momento angolare
Il momento angolare totale della particella
iniziale (spin+momento orbitale) prima del
decadimento deve essere uguale al momento
angolare totale di tutte le particelle prodotte dal
decadimento.
Per esempio il momento di spin del neutrone è ½
per cui non può decadere in un protone (spin ½)
e un elettrone (spin ½) ma ….(decadimento
beta)
Radioattività – Leggi di conservazione
Conservazione della carica elettrica
La carica elettrica totale prima e dopo il
decadimento non cambia.
Conservazione del numero di massa
Il numero di massa A non cambia nel
decadimento: in alcuni processi Z e N cambiano
entrambi ma non la loro somma.
Decadimento alfa
• E’ un effetto di repulsione Coulombiana
• Alfa molto stabile e con alta energia di
legame
A
Z
X
A4
Z 2
X 
*
Decadimento alfa
Bilancio dell’energia (X all’inizio in quiete)
mXc2=mX*c2+TX* +mc2+T
(mX - mX*- m) c2= Q=TX* + T
Bilancio del momento
p= pX*
Dinamica non relativistica
Da cui ricaviamo l’energia cinetica delle alfa:
Q
4
T 
 Q(1 )
m
A
(1
)
mX *
Decadimento Alfa
T
Decadimento alfa
Il decadimento alfa è un esempio della penetrazione di
una barriera quantistica di potenziale (effetto tunnel).
L’altezza della barriera UB è
2Z  2e
UB 
4 0
R
1
2
Energia
UB
00
R
R’
~6
MeV
r
Per un nucleo pesante UB ~ 30-40MeV mentre per le
particelle alfa le energie sono tra 4 e 8 MeV
(impossibile sormontare la barriera!!!).
Decadimento alfa
La probabilità per unità di tempo  per la particella alfa di
uscire dal nucleo è la probabilità di penetrare la barriera per il
numero delle volte al secondo che la colpisce.
v 2 kL

e
2R
k
2m/  U
2
0
 E
dove R è il raggio del nucleo, v la velocità della particella alfa
L lo spessore della barriera e E l’energia della particella.
Esercizio
Partendo dalle equazioni della conservazione
dell’energia e del momento:
1. ricavare la formula per T
2. calcolare in MeV Tdel decadimento
22 6
88
Ra13 8 
Rn13 6  
22 2
86
Dm(226Ra-222Rn) = 4.007832 AMU
m(4He)=4.002603 AMU
Ra
Radio
Rn
Radon
Decadimento beta
• Nel decadimento ß un neutrone (protone) nel
nucleo si trasforma in un protone (neutrone).
• A non cambia
• Le particelle ß sono elettroni.
• L’elettrone emesso NON è un elettrone orbitale;
NON è un elettrone già presente nel nucleo
• L’elettrone è prodotto durante il processo
dall’energia disponibile
Decadimento beta
• Bilancio di energia del decadimento del neutrone
n  p  e 

Q=(mn-mp-me-m)c2=Tp+Te+T;

0.782MeV- mc2 m0
Decadimento beta
• Analogamente per il bilancio di energia in un
nucleo
A
Z
X
A
Z 1
X * e  

Q  [m ( X )  m ( X *)  me ]c
A
N Z
A
N Z 1
mN indica le masse nucleari!!
Tabulate masse atomiche!!
2
Decadimento beta
• Per convertire le masse nucleari nelle masse
atomiche tabulate
Z
m( X)  mN ( X)  Zme  
A
A
i1
Bi
c2
Ove Bi rappresenta l’energia di legame dell’i-simo elettrone


Decadimento beta
• In definitiva in termini delle masse atomiche:
Q  {[m(A X)  Zme ][m(A X*)  (Z 1)me ] me }c 2 
{ Bi  Bi *}
Z
Z 1
i1
i1
Le masse elettroniche si cancellano.
Trascurando le differenze tra le B:
Q  [m( X)  m( X*)]c
A
A
2
Decadimento beta
• Un altro decadimento beta è:
p  n  e 

Q0
• Nel caso di un nucleo il processo è possibile e il
bilancio dell’energia è per un ß+ (positrone)
Q  [m( X)  m( X*)  2me ]c
A
A
2
Notare che in questo caso le masse atomiche non si cancellano
Decadimento beta
EC = electron capture
p+e-
n+avviene solo nei nuclei
Decadimento gamma
Gran parte dei decadimenti
 e  (nella maggior parte
delle reazioni nucleari)
lasciano il nucleo in uno
stato eccitato. Questi stati
decadono
tramite
emissione di fotoni con
energia tipica 0.1-10MeV e
lunghezze d’onda tra 104 e
100 fm.
Decadimento gamma
• Bilancio energetico: un nucleo di massa M
decade con energia ∆E. La conservazione
del momento produce un rinculo del nucleo.
• L’energia cin. del nucleoTM=pM2/2M
• L’energia del  E= cp
• Si ottiene
DE  E 
E2
2Mc 2
Decadimento gamma
• Si ottiene:
DE 12
DE
E   Mc [1  (1  2
) ]  DE 
2
Mc
2Mc2
2
DE  Mc
2
DE  MeV
Mc  A x MeV A  numero di massa
2
Radioattività naturale
Tutti gli elementi sono stati creati all’intero
delle stelle (eccetto H e He) da reazioni
nucleari. Alcuni di loro hanno vite medie
che sono comparabile con l’età della terra e
sono quelli che in parte determinano la
radioattività naturale.
Un decadimento radioattivo può essere
parte di una catena fino a quando non si
raggiunge un elemento stabile
Radioattività naturale
Radioattività - Datazione
• Il C in natura è al 98,89 % 12C e per 1,18% 13C ambedue
stabili. Il 14C è radioattivo ed è formata nell’atmosfera
come risultato del bombardamento dei raggi cosmici
sull’azoto dell’atmosfera. Il tempo di dimezzamento è
5730 anni per cui ogni grammo di carbonio mostra circa
15 decadimenti per minuto (Verificate!!!!)
• Quando un organismo muore non è piu in equilibrio con il
carbone atmosferico e il suo contenuto di 14C decresce
secondo la legge del decadimento radioattivo. Pertanto
l’età di un campione è misurata dalla sua specifica attività
(attività per grammo) del suo contenuto di carbonio.
Interazione con la materia
Interazione con la materia
• Particelle cariche: perdite di energia per
interazione con elettroni. Interazione Coul.
con nuclei piccola (elettroni Zx nuclei e
pervadono volume)
• Alfa: massima energia trasferita per
collisione diretta con elettrone
• DT=T (4m/M)≈2.7keV
Range delle alfa
• Energia di ionizzazione o eccitazione
5-20eV
• Migliaia di collisioni prima di perdere
energia
•  poco deflesse da elettronitraiettoria
quasi retta
RANGE
• Range (percorso) dipende da interazione con
elettroni atomici, quindi circa inversamente prop.
alla densità.
• In genere è riportato il prodotto percorsoxdensità
in unità di mg/cm2 o g/cm2, ancora chiamato
range.
• Quindi dal range in mg/cm2 (g/cm2) occorre
dividere per la densità in mg/cm3 (g/cm3) per avere
il percorso in cm.
BETA
• Interagiscono con elettroni del mezzo come le ,
MA:
• Spesso viaggiano a velocità relativistiche
• Soffrono grandi deviazioni. Traiettoria erratica.
• Scambio proiettile-bersaglio
• Soggetti a grandi accelerazioniemissione di
radiazione (bremsstrahlung). Trascurabile
rispetto a perdite per collisioni se v/c<<1.
GAMMA
•  e X interagiscono con la materia per tre
processi:
• Effetto fotoelettrico, diffusione Compton,
creazione di coppie e+ e-.
• Effetto fotoelettrico fotone assorbito con
emissione di elettrone
Te=E -Be B=energia di legame dell’elettrone
GAMMA(Compton)
• Diffusione Compton è
il processo per cui un
fotone  collide con un
elettrone atomico e
diffonde con una
energia più bassa
mentre
l’elettrone
assume la differenza di
energia.
E
E scatt. 
1 (
E
mc
2
)(1 cos )
GAMMA (Cr. di coppie)
• Un  sparisce creando una coppia
elettrone-positrone.
• Soglia di 2mc2=1.022MeV
• Dominante per energie E>5MeV
Forze fondamentali
Chi è responsabile per il decadimento beta ?
La forza debole
La forza debole non gioca un ruolo
importante nel legame dei nuclei (per due
protoni vicini è circa 10-7 volte più debole
della forza forte tra di loro e il suo range è
più piccolo di 0.001fm) ma ciononostante è
fondamentale nella fisica delle alte energie
Forze fondamentali
• Forza gravitazionale (Moto dei corpi celesti,
meccanica newtoniana)
• Forza elettromagnetica (Equazioni di
Maxwell)
• Forza nucleare o forte
• Forza debole