Slides Lezione 12 File

Introduzione alla
psicologia
modulo: fondamenti
di psicometria
metodologia della ricerca
psicologica
Lezione 12
17/05/2017
•
•
•
•
•
•
•
•
•
•
prof. Carlo Fantoni
Autovalutazione su scale di
misura
Variabili e relazioni causali
Tipi di misure psicologiche
del comportamento
Un esempio di misura
diretta: SAM
Un esempio di misura
indiretta: detezione del
segnale
Variabili aleatorie
Distribuzione di Frequenza
e di probabilità
La distribuzione gaussiana
Regola empirica e punteggi
standard
Esempio pratico con Excel
Scienze tecniche e
psicologiche
2016-2017
mettiamoci alla prova sulle
scale di misura
che tipo di misura è
numero di film visti durante le vacanze (0, 1, 2, 3, 4)
 Quantitativa→
modalità
numerica
(non
categorie/etichette)
 Rapporti → zero assoluto + vale il rapporto (vedere
4 film significa vederne il doppio di chi ne ha visti 2)
 Discreta → assume un numero intero di possibili
modalità (non infinite possibili modalità)
possibili altri esercizi
che tipo di variabile è
1. Età (0, 1, 2, 3, 4)
2. Genere di musica preferito (rock, jazz, folk, classical)
3. Grado di felicità (molto, abbastanza, poco, per niente)
4. Tempo di denominazione (secondi)
5. Tasso di crescita di una popolazione (percentuale)




Quantitative o Qualitativa?
Nominali, ordinali, intervalli, rapporti?
Continue o discrete?
Mutabile (sconnessa, rettilinea) o variabile (discreta,
continua)?
variabili e relazioni causali
eventi osservati (caratteri)
che possono
assumere diversi valori (modalità) tra i soggetti
di un campione o di una popolazione (unità
statistica)
1. variabili indipendenti:
controllate dallo scienziato (cause di effetti)
2. variabili dipendenti:
se ne osserva la variazione al variare
sistematico delle prime
3. variabili confondenti:
non controllate dallo sperimentatore ma che
hanno un effetto sulla v. dip. (apprendimento)
soglie assolute
valore fisico minimo che determina
una reazione comportamentale
 visione: candela da 48 km in
una notte serena
 udito: orologio meccanico a 6
m in una stanza silenziosa
 gusto:
1
cucchiaino
di
zucchero in 7.5 litri di acqua
 olfatto: 1 goccia di profumo in
1 appartamento di tre stanze
 tatto: ala di un ape lasciata
cadere da un altezza di 1 cm
soglia di detezione del contrasto
 Metodo: 2 IFC
 Variabile indipedente: weber contrast (C)
 Variabile dipendente: % corrette
Il ragionamento
Capacità di ragionamento
Verbale
Numerico
Logico/Fluida
Sinonimi e contrari
Comprensione del testo
Uso del linguaggio
Incognite
Percentuali
Frazioni
Sillogismi
Serie di numeri
Serie di figure
Insiemistica
un esempio di misura diretta:
Self-Assesment Manikin
(Lang, 1980; Hodes, Cook & Lang 1985)
Piacevolezza
Completamente
infelice,
irritato,
insoddisfatto,
melanconico,
depresso
Completamente
felice,
contento,
soddisfatto,
gioioso,
speranzoso
Attivazione
Completamente
rilassato,
calmo,
inerte,
assonnato,
non attivato
Completamente
eccitato,
frenetico,
nervoso,
sveglio,
attivato
forma “Boomerang” dello
spazio delle risposte affettive
 Un set normativo di stimoli
emotivi per esperimenti su
come le emozioni
influenzano i diversi aspetti
della cognizione umana
 700 immagini, valutate
mediante la tecnica SAM in
12 blocchi separati di 60
prove ciascuno (la raccolta
dati dura da più di 10 anni)
 I punteggi sono stabili sia
per quanto riguarda la
validità intra e inter soggetti
 Forma a “boomerang”
un esempio di misura indiretta:
discriminazione tra due stati
(sensibilità e criterio di risposta)
discriminazione tra due stati
funzione cognitiva
stati
percezione sensoriale
presente / assente
riconoscimento
nuovo / vecchio
recupero dell’informazione
in memoria
rilevante / non rilevante
applicazioni
contesto
stati
diagnosi medica
malato / sano
esame radiologico
presenza / assenza
sentenza
colpevole / non colpevole
indagine di mercato
accettabile / non accettabile
Ispezione/sicurezza
presenza /assenza
Swets, J. A. (ED.) (1988b). Signal detection and recognition by human observers. New York: Wiley.
… ad esempio
ispezione
sicurezza
diagnosi
dai metodi classici alla SDT
Realtà
fisica
Realtà
sensoriale
Risposta
F
S
R
nessun controllo della relazione tra sensazione e giudizi
SDT e processi interni
Due processi interni per due parametri
F
S
sensibilità
D
criterio
R
“presente
/assente”
parallelismo psicofisiologico
continuum dell’attivazione
continuum fisico
[diametro]
parallelismo psicofisiologico
continuum dell’attivazione
[in unità sn]
continuum fisico
[diametro]
parallelismo psicofisiologico
continuum dell’attivazione
[in unità sn]
continuum fisico
[diametro]
parallelismo psicofisiologico
d’
continuum dell’attivazione
[in unità sn]
continuum fisico
[diametro]
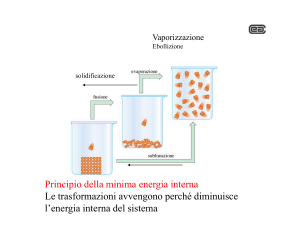
variabili aleatorie



Per definizione, un singolo evento
aleatorio o casuale non è predicibile
Tuttavia, le ripetizioni dei fenomeni
aleatori esibiscono delle regolarità.
Lo scopo della teoria della probabilità è
quello di descrivere queste regolarità
Gauss e l’ordine del disordine
0 0 0 0 0
1 0
0 0 0 0 0
Gauss e l’ordine del disordine
0 0 0 0 1 1
0
0 0 0 0 0
Gauss e l’ordine del disordine
0 0 0 0 1 1
1
0 0 0 0 0
Gauss e l’ordine del disordine
0 0 0 0 1 2
1
1 0 0 0 0
Gauss e l’ordine del disordine
0 0 1 3 5 10 5 4 0 0 0
Gauss e l’ordine del disordine
Probabilità
La ripetizione di eventi singoli e
indipendenti rivela la struttura
sottostante del fenomeno
-3 -2 -1 0 1 2 3
distanza
2

1
1  x  
fX  x  
exp  
 
2 s
 2  s  
Deviazione
standard:
2
xi    media del valore assoluto

s
degli scarti di ciascuna
n
osservazione dalla media
flusso attentivo e caso
Le traiettorie apparentemente
casuali seguite dal nostro flusso
attentivo durante l’esplorazione
rivelano la struttura sottostante
degli oggetti consegnandoci una
rappresentazione coerente e
stabile del mondo
campioni di altezza
1,61 < h < 1,63
1,59 < h < 1,61
1,57 < h < 1,59
altezza nel mondo
altezza nel mondo
campioni di altezza
1,61 < h < 1,63
1,59 < h < 1,61
Francesca Piccinini
e Simona Gioli
h = 1,85
1,57 < h < 1,59
Sara Anzanello
h = 1,92
altezza nel mondo
altezza nel mondo
probabilità e frequenza di eventi
distribuzione di
probabilità
P( xi )  0 e
n
 P( x )  1
i 1
i
F ( xi )  P( X  x)   Pxi 
Funzione di ripartizione empirica
x  xi
1
0.5
mondo
x s
x altezza
s x nel
altezza nel mondo
0
Circa il 68% dei casi
probabilità e frequenza di eventi
distribuzione di
probabilità
P( xi )  0 e
n
 P( x )  1
i 1
i
F ( xi )  P( X  x)   Pxi 
Funzione di ripartizione empirica
x  xi
1
0.5
x  2s
altezza
x  2s
x nel mondo
altezza nel mondo
0
Circa il 95% dei casi
interpretare s:
regola empirica
se l'istogramma della distribuzione ha una forma
approssimativamente campanulare:
 Circa il 68% delle osservazioni assume valori
compresi tra x  s e x  s
 Circa il 95% delle osservazioni assume valori
compresi tra x  2  s e x  2  s
 La quasi totalità delle osservazioni assume valori
compresi tra x 3  s e x  3  s
s nella distribuzione di frequenze
distribuzione normale standard: N(0;1)
qualunque punteggio è esprimibile nei termini del numero di
deviazioni standard che lo separano dalla media (z-score)
x  zs  x
xx
z
s
a ciascun valore della variabile
x può essere quindi associato
il corrispondente valore della
variabile standardizzata z,
ottenuto
applicando
la
standardizzazione
Esempio
voto in trentesimi all’esame di statistica in una
classe di 25 studenti
10
• 14 voti su 25 (56%) sono
nell’intervallo
compreso
fra ± 1 s dalla media.
• nessun voto appartiene a
più di 2 s dalla media
Come usare Excel per verificare ?
Esempio_standardizzazione
su moodle2