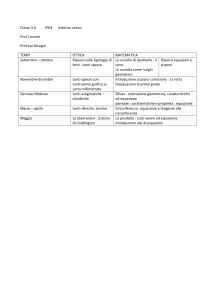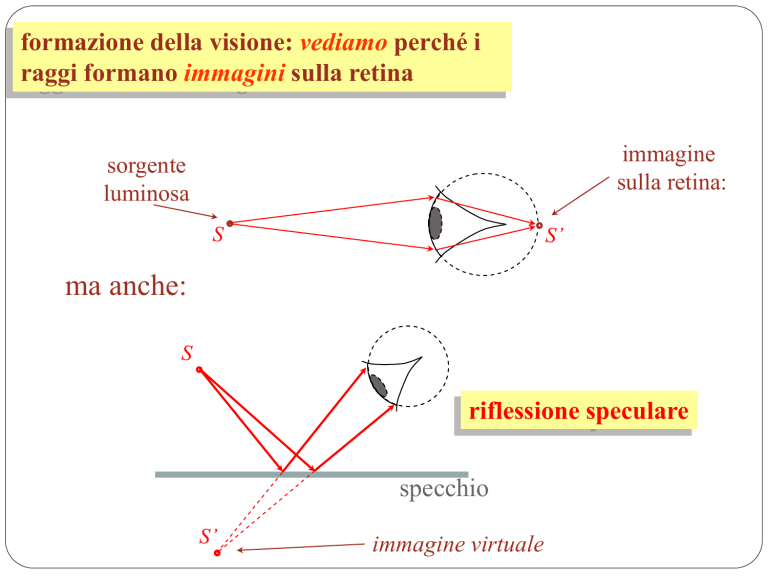
formazione della visione: vediamo perché i
raggi formano immagini sulla retina
immagine
sulla retina:
sorgente
luminosa
S’
S
ma anche:
S
riflessione speculare
specchio
S’
immagine virtuale
SORGENTI E IMMAGINI
definizioni
fascio omocentrico
(coniugato) emergente
fascio omocentrico
incidente
S
sistema
ottico
oggetto
S’
immagine
punti
coniugati
definizioni
reale
virtuale
oggetto
centro dei
raggi incidenti
centro del
prolungamento
dei raggi incidenti
immagine
centro dei
raggi emergenti
centro del
prolungamento
dei raggi emergenti
sorgenti e immagini
immagine
virtuale
S
oggetto
reale
S’
S
immagine
reale
S’
oggetto
reale
immagine
specchio virtuale
oggetto
reale
S
S’
sorgenti e immagini
immagine
reale
S’
S’
oggetto
virtuale
immagine
virtuale
S’
S
oggetto
virtuale
definizioni
si noti la differenza:
punto oggetto
punto immagine
sistema
ottico
S
S’
sistema stigmatico
sistema
ottico
S
punto oggetto
sistema astigmatico
immagine
aberrazione
esempio
Il diottro piano
acqua
n = 1.33
acqua
n = 1.33
Dh
la moneta “avvicinata”
la matita “spezzata”
esempio
Il diottro piano
LE LENTI
rifrazione e formazione dell’immagine da diottri successivi
n2
n1
n3
S2’= S3
S1
S3’
D1
D2
D3
n1
S1’= S2
le lenti
combinazioni di più diottri: le lenti
semplici
composte
(esempio)
le lenti
tipi di lenti
pianoconvesse
pianoconcave
biconvesse
biconcave
menisco
menisco
(concavaconvessa) (convessaconcava)
le lenti
S
F’
O
F
S’
se la lente è sottile:
s
s’
Si può scrivere la seguente equazione:
1
1
1
1
( n 21 1 )
s
s'
R2
R1
equazione del
costruttore di lenti
lenti sottili
1
1
1
1
equazione del
costruttore di lenti
( n 21 1 )
s
s'
R2
R1
ponendo rispettivamente: s, s’
= ∞ troviamo che:
1
s'
1
1
1
( n 21 1 )
f'
R2
R1
f = f’: punti focali
equidistanti da O
1
1
s
f
( n 21
1
1
1 )
R2
R1
F’
F
F
F’
1
1
1
1
1
( n 21 1 )
s
s'
R2
f
R1
lenti sottili
Si può quindi scrivere:
1
1
1
s
s'
f
<
> 0
equazione delle lenti
lente positiva/negativa
1
potenza
diottrica
f
F’
F
lente positiva
F
lente negativa
lenti sottili
S
1
1
1
s
s'
f
ingrandimento laterale:
y'
m
y
s'
s
F
O
1
potenza
diottrica
f
F
S’
s
s’
piani focali
attenzione al segno di R!
1
f
1
( n 21 1 )
R1
f>0
pianoconvesse
biconvesse
1
R2
convergenti
(positive)
concaveconvesse
(menisco)
f<0
divergenti
(negative)
pianoconcave
biconcave
concaveconvessa
(menisco)
lenti sottili
1
1
1
s
s'
f
per il tracciamento si usano due dei tre raggi principali:
F
O
S
S’
F
s
s’
lente positiva o convergente
lenti sottili
1
1
1
s
s'
f
per il tracciamento si usano due dei tre raggi principali:
y’
y
S
S’
F
F
s
s’
lente negativa o divergente
costruzioni delle immagini
lenti sottili convergenti (positive)
I)
S
oggetto reale,
immagine reale
F
y
y’
F
S’
y
obiettivo di
macchina fotografica
| m| << 1
F
F
pellicola
y
F
F
obiettivo di
proiettore
| m| >> 1
costruzioni delle immagini
lenti sottili convergenti (positive)
le immagini reali possono essere viste direttamente dall’occhio
S
F
y
F
S’
S
F
y
F
oppure visualizzate (“proiettate”) su uno schermo
costruzioni delle immagini
lenti sottili convergenti (positive)
II)
y’
y
oggetto reale,
immagine virtuale
F
F
lente di ingrandimento,
oculari microscopio, telescopio
III)
y
F
y’ F
oggetto virtuale,
immagine reale
costruzioni delle immagini
lenti sottili divergenti (negative)
I)
y
F
F
oggetto reale,
immagine virtuale
F
oggetto virtuale,
immagine reale
y’
II)
F
y y’
III)
F
y’ F
y
oggetto virtuale,
immagine virtuale
oculare cannocchiale
Aberrazioni delle lenti
si noti che:
fuori dall’appross. parassiale si ha l’aberrazione sferica:
il fuoco è su un segmento
Aberrazioni delle lenti
si noti che:
anche nella approssimazione parassiale la dispersione
provoca la:
n n ( )
F
F’
aberrazione cromatica
f f ( )
lenti sottili
aberrazione cromatica
n n( )
F
F’
f f ( )
parzialmente correggibile con lenti composte
Riepilogo: le lenti sottili
1
1
1
1
1
( n 21 1 )
s
s'
R2
f
R1
1
1
1
s
s'
f
y'
m
y
s'
s
equazione del
costruttore di lenti
equazione delle lenti
ingrandimento laterale
SISTEMI E STRUMENTI OTTICI
L’occhio umano
Umor acqueo
Umor vitreo
oggetto esteso
Disegno schematico dell’occhio umano
Funzionamento: lente convergente caso I)
S
F’
y
y’
F
S’
oggetto reale,
immagine reale
L’occhio umano: sensori e sensibilità
Umor vitreo
120.000.000 di
bastoncelli
(visione notturna
acromatica)
7.000.000 di
coni
(visione diurna
cromatica)
Curve di sensibilità
3 tipi di coni
teoria del tri-stimolo
per la percezione del colore
l’occhio umano
il processo di accomodamento:
oggetto all’infinito
oggetto a
distanza finita
l’occhio umano
i più comuni difetti della visione:
il bulbo oculare è
“allungato”
il potere di
accomodamento
è limitato
l’occhio umano
nel processo di visione distinta naturale:
y
0
y’
d
definiamo:
y
y
0 atan
d
d
grandezza angolare (apparente)
15 cm d
ma la visione è più distinta per d = d0 25 cm
6.2a Il microscopio semplice (lente di ingrandimento)
y’
’
y
F
d’
si confronti con la situazione di visione distinta naturale:
y
0
d0
definiamo ingrandimento angolare:
'
M
0
y ' d 0
y d '
tan
M
d0
f
Il microscopio composto
oculare
s’
s
y
O
F1’
F2
y’=y0
F1
y0’
’
F2’
obiettivo
d’
'
M
0 '
y 0 ' d 0 y '
y'
y
y 0 d ' y
tipic. mob 50 200, Moc 5 10
- mob Moc
M 200 2000