file

Le funzioni goniometriche e i vettori
Come si misurano gli angoli
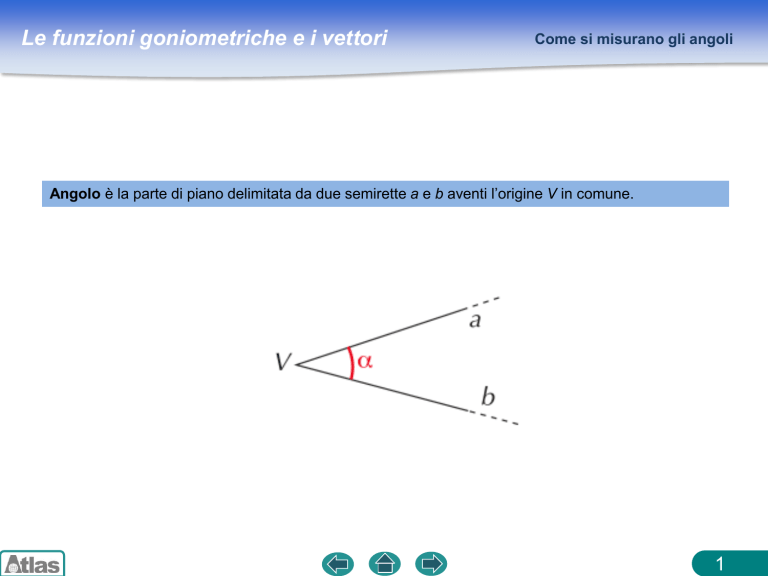
Angolo è la parte di piano delimitata da due semirette a e b aventi l’origine V in comune.
1
Le funzioni goniometriche e i vettori
Come si misurano gli angoli
Gli angoli si possono misurare in gradi oppure radianti.
Misurare in gradi
Il grado sessagesimale viene definito come la trecentosessantesima parte dell’angolo giro:
(1° = 1/360 di angolo giro)
Il grado non ha multipli, ma ha sottomultipli:
• il primo, corrispondente a 1/60 di grado, che ha come simbolo un apice;
• il secondo, corrispondente a 1/60 di primo, cioè a 1/3600 di grado, che ha come simbolo un
doppio apice.
ESEMPI
Esprimiamo in gradi, primi e secondi l’angolo 32,48°
32,48° = 32° + 0,48° = 32° + 0,48°  60 = 32° 28,8’ = 32° + 28’ + 0,8 60 = 32°28’48”
Esprimiamo in gradi, nella forma decimale, l’angolo 15°32’40”
15°32’40” = 15° + 32  (1/60)° + 40  (1/3600)° ≈ 15,544 (al millesimo di grado)
La conversione dai gradi alla forma decimale e quella contraria possono essere svolte con la
calcolatrice scientifica.
2
Le funzioni goniometriche e i vettori
Come si misurano gli angoli
Dato un angolo α di vertice C e la circonferenza avente centro nel
vertice dell’angolo e raggio r, si assume come misura di α il rapporto
tra la lunghezza
l dell’arco AB sotteso da α e il raggio r :
ℓ
misura di a =
r
Tale ampiezza non dipende dal raggio della circonferenza scelta. L’unità di questo nuovo sistema di
misurazione si chiama radiante.
Un radiante è l'ampiezza di un angolo al quale corrisponde un arco AB la cui lunghezza
raggio r.
l
è uguale al
ESEMPIO
lunghezza circonferenza rettificata 2p r
=
= 2p
raggio
r
Quindi un angolo piatto misura π e un angolo retto π/2
3
Le funzioni goniometriche e i vettori
Come si misurano gli angoli
In generale per passare da un sistema di misura ad un altro, si usa la proporzione
y : x = 360° : 2p
Dove
x : misura dell’angolo in radianti
y : misura dell’angolo in gradi
ESEMPI
Troviamo la misura in radianti di un angolo di 32°15’
32°15' = 32,25°
x = 32,25 ×
®
32,25° : x = 360° : 2p
2p
» 0,56287
360
p
Troviamo la misura in gradi di un angolo di
y:
p
15
= 360° : 2p
®
y =
360 ×
2p
15
p
15 = 12°
4
Le funzioni goniometriche e i vettori
Le funzioni goniometriche fondamentali
Considerata la circonferenza goniometrica (avente centro nell’origine di un sistema di assi cartesiani
ortogonali e raggio unitario ed un angolo α avente vertice nell’origine e un lato coincidente con il
semiasse positivo delle ascisse, indicato con P il punto di intersezione con la circonferenza,
chiamiamo:
• seno dell’angolo α, e scriviamo sin α, la funzione che ad α associa l’ordinata del punto P:
sin α = yp
• coseno dell’angolo α, e scriviamo cos α, la funzione che ad α associa l’ascissa del punto P:
cos α = xp
5
Le funzioni goniometriche e i vettori
Le funzioni goniometriche fondamentali
Qualunque sia l’ampiezza dell’angolo α, sia sin α che cos α non possono assumere valori inferiori a -1 o
valori superiori a 1; valgono quindi le limitazioni:
-1£ sina £ 1
-1£ cosa £ 1
6
Le funzioni goniometriche e i vettori
Le funzioni goniometriche fondamentali
Riprendiamo la circonferenza goniometrica e tracciamo la
retta t ad essa tangente nel punto A(1,0); dato un angolo
orientato α, sia Q il punto in cui il secondo lato di α interseca
la retta t.
Chiamiamo tangente dell’angolo α, e scriviamo tan α, la
funzione che ad α associa l’ordinata del punto Q:
tan α = yQ
•
La tanα non esiste se
a = 90° Ù a = 270°
7
Le funzioni goniometriche e i vettori
Le relazioni fondamentali
Due relazioni fondamentali legano tra loro le funzioni goniometriche:
1^ relazione fondamentale della goniometria
2^ relazione fondamentale della goniometria
sin2 a + cos2 a = 1
sina
tana =
cos a
per qualunque angolo α
con cos a ¹ 0
cioè
a¹
p
2
+kp
8
Le funzioni goniometriche e i vettori
I valori delle funzioni goniometriche fondamentali
Dalle relazioni tra i lati dei triangoli rettangoli con gli angoli di 30° e 60° o di 45° si ottengono i
valori delle funzioni goniometriche fondamentali per angoli particolari.
9
Le funzioni goniometriche e i vettori
I triangoli rettangoli
In ogni triangolo rettangolo, la misura di un cateto è uguale:
•al prodotto della misura dell’ipotenusa per il seno dell’angolo opposto al cateto stesso.
•al prodotto della misura dell’ipotenusa per il coseno dell’angolo acuto adiacente al cateto
stesso.
•al prodotto della misura dell’altro cateto per la tangente dell’angolo opposto al cateto da
determinare.
10
Le funzioni goniometriche e i vettori
I triangoli rettangoli
ESEMPIO
Determiniamo la misura dell’ipotenusa di un triangolo rettangolo sapendo che un cateto è lungo
3 cm e l’angolo ad esso opposto è ampio 55°.
Utilizziamo la formula
Si ha quindi c =
a = c × sina e determiniamo la formula inversa: c =
a
sina
3
= 3,66cm
sin55°
11
Le funzioni goniometriche e i vettori
Scalari e vettori
Una grandezza scalare è individuata da un numero.
Una grandezze vettoriale è definita da:
•
Una direzione, che indica la retta lungo la quale agisce
•
Un verso, che indica il senso di percorrenza della
retta che rappresenta la direzione
•
Un’intensità o modulo, che è il valore
numerico che rappresenta la misura
della grandezza
12
Le funzioni goniometriche e i vettori
I vettori nel piano cartesiano
Un vettore
nel piano cartesiano può essere scomposto in due vettori lungo gli assi cartesiani
la cui somma dà il vettore
stesso.
Noto l’angolo α che il vettore forma con il semiasse positivo delle ascisse, i moduli delle due
componenti si trovano con le seguenti formule:
v x = v cos a
E per il teorema di Pitagora
v y = v sina
v = v 2x +v 2y
13
Le funzioni goniometriche e i vettori
Determiniamo le componenti del vettore
direzione positiva dell’asse x.
vy
I vettori nel piano cartesiano
di modulo 6 che forma un angolo di 65° rispetto alla
6
65°
vx
Applicando le formule
v x = v cos a
v y = v sina otteniamo:
v x = 6cos65° = 2,54
e
v y = 6sin65° = 5,44
14
Le funzioni goniometriche e i vettori
Dati due vettori
•
somma di due vettori
•
differenza di due vettori
•
prodotto del vettore
Le operazioni con i vettori
nel piano cartesiano
e uno scalare k, definiamo
il vettore
il vettore
per lo scalare k il vettore
ESEMPI
Dati i vettori
, determina la somma e la differenza dei due vettori e il vettore
Determiniamo la somma:
Determiniamo la differenza:
Infine il vettore
vale
15