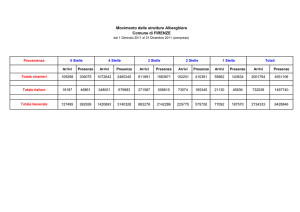
MISURA DI NUMERO DI ARRIVI DI
RAGGI COSMICI IN UN CERTO Dt
ANALISI DATI
Gruppo di Ricerca del L.S.S. “G. Bruno”
COSA ABBIAMO FATTO:
Abbiamo misurato ripetutamente il numero di
eventi che si verificano in un certo Dt
Sono eventi casuali. Nel senso che non v’è
connessione tra un evento e un altro (l’arrivo di
una particella non influenza gli arrivi successivi)
classi di arrivi
FREQUENZA
0
1
1
0
2
3
3
9
4
23
5
50
Rivelatore utilizzato: Cosmic Box, rivelatore
a scintillazione; in coincidenza.
6
81
7
88
Misura di arrivi in Dt = 10 s
8
107
9
115
10
98
11
57
12
37
13
28
14
26
15
14
16
11
17
4
18
4
19
3
20
1
I DATI DI CUI DISPONIAMO SONO …
Unione di dati di due gruppi (circa 800 dati)
COSA POSSIAMO OTTENERE DA
QUESTI DATI?
classi di arrivi
FREQUENZA
0
1
1
0
2
3
3
9
4
23
5
50
6
81
7
88
8
107
9
115
10
98
11
57
12
37
13
28
120
14
26
100
15
14
80
16
11
17
4
18
4
19
3
20
1
in prima battuta possiamo ottenere due
informazioni:
a) il numero medio di arrivi nel Dt,
b) Un grafico: frequenza vs. numero di arrivi
a) Numero medio di arrivi: m = 8,9 arrivi
in 10s
m ( classe freq.) /( n misure fatte)
b) Grafico: frequenza vs. numero di arrivi
FREQUENZA vs. N° DI ARRIVI
Cosmic Box - Dt = 10s
FREQUENZA
140
60
40
20
0
0
5
10
15
N° ARRIVI
20
25
Osservazione: la distribuzione che otteniamo sperimentalmente
ha una forma che si intravede chiaramente. Si intravede un
ordine sotto il grafico che abbiamo ottenuto.
Questo ordine lascia sperare che si possa descrivere
matematicamente il nostro grafico, con una legge
matematica.
Intanto rendiamo più generale il nostro grafico. Dividiamo tutte
le ordinate del nostro grafico (frequenza di un certo numero di
arrivi) per il numero di arrivi totali. In tal modo otteniamo la
probabilità con cui un certo numero di arrivi si verifica.
(esempio: se l’evento 5 arrivi in 10s ha una probabilità di 0,06
significa che su un numero molto grande di misure mi aspetterò
che il 6% delle volte si verifichino 5 arrivi)
FREQUENZA vs. N° DI ARRIVI
Cosmic Box - Dt = 10s
PROBABILITA' vs. N° ARRIVI
0,16
140
0,14
PROBABILITA'
FREQUENZA
120
100
80
60
0,12
0,1
0,08
0,06
40
0,04
20
0,02
0
0
0
5
10
15
N° ARRIVI
20
25
0
5
10
15
N° ARRIVI
20
25
Questa curva si chiama DISTRIBUZIONE DI PROBABILITA’
Mi dice
come si distribuiscono le probabilità dei vari ARRIVI in un esperimento come il nostro.
Cioè mi dice
con quale probabilità il mio singolo esperimento di misura (arrivi in un certo Dt) avrà un
certo esito.
PROBABILITA' vs. N° ARRIVI
0,16
PROBABILITA'
0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
0
5
10
15
N° ARRIVI
20
25
Ogni volta che in una misura ripetuta si ha una distribuzione di
probabilità che ci dice con quale probabilità si verificherà un certo
esito della nostra singola misura…
…possiamo anche pensare che esista una DISTRIBUZIONE LIMITE
Cioè della distribuzione che otterremmo se ripetessimo la nostra
singola misura INFINITE volte.
LA ATTUALE PICCOLA SFIDA CONSISTE IN QUESTO:
Chiederci quale sia la nostra distribuzione limite.
Possiamo provare con la distribuzione di Poisson
1781-1840
La distribuzione di Poisson è la distribuzione limite
•del numero di telefonate ricevute da un centralinista in un’ora;
•del numero di errori tipografici per pagina di battitura di una segretaria;
Ogni telefonata ricevuta da una centralinista in un certo tempo non
influenza l’arrivo delle successive chiamate, un po’ come l’arrivo di una
particella nel nostro rivelatore non influenza l’arrivo delle successive.
Piccola parentesi da tenere a mente.
Ci servirà più avanti
Se la nostra distribuzione limite risultasse essere la distribuzione di Poisson
allora si può dimostrare che sarebbe corretto dire che
Numero di arrivi in 10 s misurati dalla cosmic box =
n arrivi medio n arrivi medio
La distribuzione di Poisson, come tutte le ditribuzioni limite mi permette di
sapere con quale probabilità avremo un certo esito della nostra singola
misura.
Per esempio con quale probabilità la centralinista riceverà 1 tel. in un’ora, o 2
tel in un’ora, …
Nel nostro caso dovrebbe dirci con quale probabilità conteremo 0 raggi
cosmici con la Cosmic Box in 10s o 1 raggi in 10s, o 2, …
Per dirci tutte queste cose la distribuzione di Poisson ha bisogno di un solo
dato: il valor medio della nostra singola misura (es.: il n° di tel. In un’ora o, nel
nostro caso, il numero di arrivi in 10s cioè 8,9 arrivi). Ecco l’equazione della
distribuzione di Poisson
Per dirci tutte queste cose la distribuzione di Poisson ha bisogno di
un solo dato: il valor medio della nostra singola misura (es.: il n° di
tel. In un’ora o, nel nostro caso, il numero di arrivi in 10s cioè 8,9
arrivi). Ecco l’equazione della distribuzione di Poisson
P ( n) e
m
n
m
n!
n = numero di eventi in un certo intervallo di tempo
m = valore medio del numero di eventi in un certo intervallo di tempo
e = numero di Nepero, 2,718281828…
n! = 1*2*3*….*n
Noi conosciamo il valor medio di ogni nostra singola misura proprio grazie al
vostro esperimento!
E’
m =
8,9
arrivi
Possiamo provare a vedere se la curva di equazione
P ( n) e
8, 9
n
8,9
n!
si accorda abbastanza bene con i nostri dati.
Probabilità arrivi raggi cosmici in 10s (COSMIC BOX)
da UNIONE dati di 2 gruppi
0,16
0,14
Probabilità
0,12
0,1
0,08
0,06
0,04
0,02
0
0
5
15
10
20
25
N° arrivi
Distribuzione di Poisson con valor medio
pari a 8,9
Probabilità arrivi raggi cosmici in 10s (COSMIC BOX)
da UNIONE dati di 2 gruppi
0,16
0,14
Probabilità
0,12
0,1
0,08
0,06
0,04
0,02
0
0
5
10
15
20
25
N° arrivi
Potremmo dire che la distribuzione di Poisson con media 8,9 assomiglia alla
nostra distribuzione. Ma qualcuno potrebbe anche dire che non ci assomiglia.
C’è qualche strumento matematico che ci permette di capire se è corretto
pensare che la nostra misura si distribusca secondo un andamento poissoniano?
NB. Ciò significa che se ripetessimo INFINITE volte la nostra misura singola
(quante particelle in 10s) i vari esiti possibili (0 arrivi, 1 arrivo, ecc..) si
verificherebbero con una probabilità data dalla poissoniana rappresentata nel
grafico
C’è qualche strumento matematico che ci permette di capire se è corretto
pensare che la nostra misura si distribusca secondo un andamento
poissoniano?
La risposta è … SI’.
Probabilità arrivi raggi cosmici in 10s (COSMIC BOX)
da UNIONE dati di 2 gruppi
0,16
0,14
Probabilità
0,12
0,1
0,08
0,06
0,04
0,02
0
0
5
10
15
N° arrivi
20
25
Il TEST del c2
classi di arrivi
FREQUENZA
0
1
1
0
2
3
3
9
4
23
5
50
6
81
7
88
8
107
9
115
10
98
11
57
12
37
13
28
14
26
15
14
16
11
17
4
18
4
19
3
20
1
Noi abbiamo questi dati.
Per ogni classe di arrivo abbiamo una
frequenza osservata (cioè misurata
sperimentalmente)
Supponiamo che la nostra
distribuzione limite sia la Poisson
con m = 8,9.
Dire questo significa attendersi
che, ripetendo infinite volte la
nostra misura, avremmo ottenuto
la Poisson (con m=8,9).
Possiamo allora calcolarci le
frequenze attese utilizzando la
Poisson (con m=8,9).
classi di arrivi
FREQUENZA
OSSERVATA
FREQUENZA ATTESA
0
1
0
Ottenute dall’esperimento
1
0
1
(Quindi osservate)
2
3
4
3
9
12
4
23
27
5
50
49
6
81
72
7
88
91
8
107
101
9
115
100
10
98
89
11
57
72
12
37
53
Ottenute dalla
distribuzione limite di
Poisson (con m = 8,9)
13
28
36
(Quindi attese)
14
26
23
15
14
14
16
11
8
17
4
4
18
4
2
19
3
1
20
1
0
ESPERIMENTO
DISTRIBUZIONE LIMITE
classi di arrivi
FREQ.OSSERVATA
FREQUENZA ATTESA
0
1
0
1
0
1
2
3
4
Ricordiamoci la nostra domanda:
3
9
12
4
23
27
5
50
49
6
81
72
E’ corretto pensare che le
frequenze osservate si
distribuiscano secondo un
andamento poissoniano?
7
88
91
8
107
101
9
115
100
10
98
89
11
57
72
12
37
53
13
28
36
14
26
23
15
14
14
16
11
8
17
4
4
18
4
2
19
3
1
20
1
0
ESPERIMENTO
DISTRIBUZIONE LIMITE
classi di arrivi
FREQ.OSSERVATA
Fo
FREQUENZA ATTESA
Fa
0
1
0
1
0
1
2
3
4
3
9
12
4
23
27
5
50
49
6
81
72
7
88
91
8
107
101
9
115
100
10
98
89
11
57
72
12
37
53
E allora che facciamo? …
13
28
36
14
26
23
…ci calcoliamo le diffrenze
15
14
14
16
11
8
17
4
4
18
4
2
19
3
1
20
1
0
E’ abbastanza chiaro che la
risposta si celi nella differenza tra
le freq. Attese, Fa, e le freq.
Osservate, Fo.
In altri termini se le frequenze
attese differiscono troppo da
quelle osservate le probabilità
del nostro esperimento NON si
distribuiranno poissonianamente
Fa –Fo
…
ESPERIMENTO
classi di arrivi
DISTRIBUZIONE LIMITE
FREQ.OSSERVATA FREQUENZA ATTESA
Fo
Fa
Fa – Fo
0
1
0
-1
1
0
1
1
2
3
4
1
3
9
12
3
4
23
27
4
5
50
49
-1
6
81
72
-9
7
88
91
3
8
107
101
-6
9
115
100
-15
10
98
89
-9
11
57
72
15
12
37
53
16
13
28
36
8
14
26
23
-3
15
14
14
0
16
11
8
-3
17
4
4
0
18
4
2
-2
19
3
1
-2
20
1
0
-1
Se queste differenze sono
grandi dobbiamo pensare che
Poisson NON sia la
distribuzione limite!
Ma quanto grandi?
Qual è il termine di paragone
per decidere se le differenze
sono grandi?
…silenzio…
Questo è il punto più
delicato dell’intera storia
che vi stiamo raccontando
ESPERIMENTO
classi di arrivi
DISTRIBUZIONE LIMITE
FREQ.OSSERVATA FREQUENZA ATTESA
Fo
Fa
Fa – Fo
0
1
0
-1
1
0
1
1
2
3
4
1
3
9
12
3
4
23
27
4
5
50
49
-1
6
81
72
-9
7
88
91
3
8
107
101
-6
9
115
100
-15
10
98
89
-9
11
57
72
15
12
37
53
16
13
28
36
8
14
26
23
-3
15
14
14
0
16
11
8
-3
17
4
4
0
18
4
2
-2
19
3
1
-2
-1
Immaginiamo di ripetere molte
volte l’esperimento che avete
fatto voi. Cioè immaginiamo che
tanti gruppi come il vostro
abbiano lavorato per un’ora con
lo stesso rivelatore e per lo
stesso Dt.
Allora avremmo tante colonne di
Fo e ciascuna Fo di ciascun
gruppo non sarà prefettamente
identica a quella degli altri
gruppi. Allora ogni Fo di ciascun
gruppo si potrà verificare con
una certa probabilità,
Ma secondo quale distribuzione
di probabilità? La poissoniana!
Perché il fatto che ogni gruppo
abbia misurato una certa Fo
piuttosto che un’altra è un
evento causale e ogni misura Fo
di ciascun gruppo non influenza
le altre.
ESPERIMENTO
classi di arrivi
DISTRIBUZIONE LIMITE
FREQ.OSSERVATA FREQUENZA ATTESA
Fo
Fa
Fa – Fo
0
1
0
-1
1
0
1
1
2
3
4
1
3
9
12
3
4
23
27
4
5
50
49
-1
6
81
72
-9
7
88
91
3
8
107
101
-6
9
115
100
-15
10
98
89
-9
11
57
72
15
12
37
53
16
13
28
36
8
14
26
23
-3
15
14
14
0
16
11
8
-3
17
4
4
0
18
4
2
-2
19
3
1
-2
-1
Allora se un certo Fo si
distribusice poissonianamente il
suo valor medio sarà Fa.
Inoltre Fo sarà compreso entro
l’intervallo
Fa
Fa
La situazione è questa:
Fa Fa
Fo
Fa
Fa Fa
F
Fa
Ecco qual è il termine di paragone per le differenza Fo – Fa .
La differenza Fo – Fa deve essere dello stesso ordine di grandezza di
FA
Quindi per sapere se gli esiti del nostro esperimento si distribuiscono
poissonianamente dobbiamo controllare se le differenze Fo – Fa
sono piccole o grandi rispetto a
FA
Fo Fa
Dobbiamo quindi valutare il rapporto
Fa
A noi conviene valutare i rapporti per ogni dato al quadrato
( Fo Fa ) 2
Fa
e poi sommarli tutti. Se le nostre frequenze si distribuiscono
poissonianamente ci dobbiamo aspettare che
( Fo Fa ) 2
Fa
( Fo Fa ) 2
Fa
1 dato
( Fo Fa ) 2
...
Fa
2 dato
tale somma (il c2 )assuma un valore con lo stesso ordine di
grandezza di n
n
n dato
Per noi n = 21
c2 = 35
Altro modo per rendersi conto se la distribuzione di Poisson è la nostra distribuzione
Limite è questo: inserire nel grafico le barre d’errore….
Probabilità arrivi raggi cosmici in 10s (COSMIC BOX)
da UNIONE dati di 2 gruppi
0,18
0,16
Probabilità
0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
0
5
10
15
N° arrivi
20
25