La variabile casuale poissoniana
nell'ambito degli arrivi dei raggi cosmici
Obiettivo: verificare che gli arrivi dei raggi cosmici seguono
una distribuzione poissoniana.
−
P x =
e
x!
x
Strumenti utilizzati
Contatore Geiger
Cosmic Box (CB)
Che cosa abbiamo fatto?
Abbiamo misurato
ripetutamente il numero
degli arrivi dei raggi
cosmici in un Dt = 5s.
Durata esperimento = 1 ora
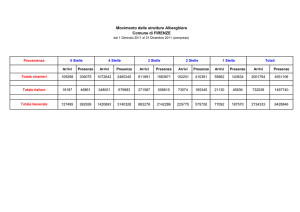
Dati totali acquisiti = 647
N° medio arrivi = 4,51
N° raggi in Dt = 5s
Frequenze osservata
0
3
1
35
2
82
3
99
4
133
5
118
6
72
7
49
8
20
9
21
10
4
11
4
12
4
13
2
14
0
15
1
Grafico
140
120
F
100
r
e
q 80
u
e 60
n
z 40
e
Frequenze
osservate
20
0
0
2
4
6
8
10
Classi di arrivi
12
14
16
Grafico
140
120
F
100
r
e
q 80
u
e 60
n
z 40
e
Frequenze
osservate
20
0
0
2
4
6
8
10
Classi di arrivi
12
14
16
Grafico
140
120
−
F
100
r
e
q 80
u
e 60
n
z 40
e
P x =
e
x
Frequenze
attese
Frequenze
osservate
x!
20
0
0
2
4
6
8
10
Classi di arrivi
12
14
16
Il test del
Domanda: come facciamo a sapere se le nostre
frequenze seguono una distribuzione poissoniana?
Risposta: il test del
E' uno strumento matematico che confronta le frequenze
osservate con le frequenze attese e fornisce un indice di
affidabilità ai dati ottenuti.
2
ai
0i
2
=∑
F −F
Fo
i
I gradi di libertà e il
Il grado di libertà (DF) è definita: DF = n°classi - 2
Il migliore è 0.
Avendo il DF e il sono in grado di dire,
attraverso una tavola dei valori critici, la
probabilità per cui i miei dati seguono una
distribuzione di Poisson.
Risultati ottenuti Cosmic Box
DF = 14
I nostri seguono una distribuzione di Poisson con
una probabilità di circa 3%
Risultati ottenuti contatore Geiger
DF = 4
I nostri seguono una distribuzione di Poisson con
una probabilità di circa 47%
Dati MRPC (1 giorno)
Dati MRPC (1 mese)
Conclusioni
Gli arrivi dei raggi cosmici seguono
parzialmente o non seguono la distribuzione di
Poisson secondo il calcolo del
Le condizioni atmosferiche influenzano gli arrivi
dei raggi cosmici
Valore didattico dell'esperimento