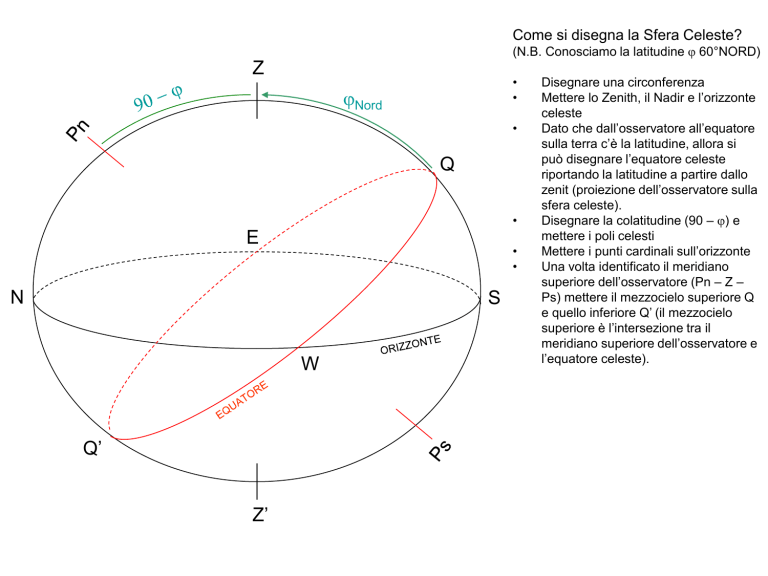
Come si disegna la Sfera Celeste?
(N.B. Conosciamo la latitudine j 60°NORD)
Z
•
•
jNord
•
Q
•
E
•
•
N
S
W
Q’
Z’
Disegnare una circonferenza
Mettere lo Zenith, il Nadir e l’orizzonte
celeste
Dato che dall’osservatore all’equatore
sulla terra c’è la latitudine, allora si
può disegnare l’equatore celeste
riportando la latitudine a partire dallo
zenit (proiezione dell’osservatore sulla
sfera celeste).
Disegnare la colatitudine (90 – j) e
mettere i poli celesti
Mettere i punti cardinali sull’orizzonte
Una volta identificato il meridiano
superiore dell’osservatore (Pn – Z –
Ps) mettere il mezzocielo superiore Q
e quello inferiore Q’ (il mezzocielo
superiore è l’intersezione tra il
meridiano superiore dell’osservatore e
l’equatore celeste).
Come si disegna la Sfera Celeste?
(N.B. Conosciamo la latitudine j 60°SUD)
Z
•
•
jSud
•
Q
•
W
•
•
S
N
E
Q’
Z’
Disegnare una circonferenza
Mettere lo Zenith, il Nadir e l’orizzonte
celeste
Dato che dall’osservatore all’equatore
sulla terra c’è la latitudine, allora si
può disegnare l’equatore celeste
riportando la latitudine a partire dallo
zenit (proiezione dell’osservatore sulla
sfera celeste).
Disegnare la colatitudine (90 – j) e
mettere i poli celesti
Mettere i punti cardinali sull’orizzonte
Una volta identificato il meridiano
superiore dell’osservatore (Pn – Z –
Ps) mettere il mezzocielo superiore Q
e quello inferiore Q’ (il mezzocielo
superiore è l’intersezione tra il
meridiano superiore dell’osservatore e
l’equatore celeste).
Determinazione delle coordinate
ALTAZIMUTALI di un astro
1.
2.
Z
jNord
3.
z
4.
Q
5.
E
h
N
S
Z
Az
W
Q’
6.
Posizionare l’astro
Disegnare il cerchio verticale passante
per l’astro dallo zenit all’orizzonte.
L’ALTEZZA (h) è l’arco di cerchio
verticale contato da 0° a 90°
dall’orizzonte fino all’astro
La DISTANZA ZENITALE (z) è l’arco
di cerchio verticale contato dallo zenit
all’astro (è sempre complementare
dell’altezza)
L’AZIMUTH (AZ) è l’arco di orizzonte
contato sempre da NORD in senso
orario da 0° a 360° (N-E-S-W-N) fino
al verticale dell’astro (piede dell’astro
sull’orizzonte)
L’ANGOLO AZIMUTALE (Z) è l’arco di
orizzonte contato dal punto cardinale
con lo stesso nome del polo elevato,
verso E o verso W (percorso più
breve) da 0° a 180° fino al verticale
dell’astro (piede dell’astro
sull’orizzonte). Ha un prefisso (N-S) e
un suffisso (E-W)
Nell’esempio del disegno
• h = 50°
Z’
• z = 40°
• Az = 290°
• Z = N 70 W
Determinazione delle coordinate
LOCALI ORARIE di un astro
1.
2.
Z
jNord
3.
p
Q
4.
d
Pw
E
N
t
5.
S
6.
W
Q’
Posizionare l’astro
Disegnare il meridiano passante per
l’astro dal polo elevato (Polo Nord)
all’equatore.
La DECLINAZIONE (d) è l’arco di
meridiano contato da 0° a 90° (verso
Nord o Sud) dall’equatore fino
all’astro. Ha un suffisso N/S.
La DISTANZA POLARE (p) è l’arco di
meridiano contato dal polo elevato
all’astro (per astri nell’emisfero
opposto al segno della latitudine è
maggiore di 90°)
L’ANGOLO ORARIO (t) è l’arco di
equatore contato da 0° a 360° a
partire dal Mezzocielo Superiore
SEMPRE verso W, fino al meridiano
per l’astro (piede dell’astro
sull’equatore.
L’ANGOLO AL POLO (P) è l’arco di
equatore contato mezzocielo
superiore, verso E o verso W
(percorso più breve) da 0° a 180° fino
al meridiano dell’astro (piede dell’astro
sull’orizzonte). Ha un suffisso (E-W)
Nell’esempio del disegno
• d = 55°N
Z’
• p = 35°
• t = 75°
• P = 75 W
Nella figura sono riportate sia le coordinate
ALTAZIMUTALI, sia quelle LOCALI ORARIE.
•
•
Z
j
Analizziamo la figura nella sua completezza
Consideriamo la porzione di sfera indicata nel
rettangolo tratteggiato.
Il triangolo sferico evidenziato di chiama
“TRIANGOLO DI POSIZIONE”.
•
z
p
Q
d
Pw
E
t
h
N
S
Z
Az
W
Q’
Z’
Z
P
A
Nel Triangolo di posizione
(particolare ingrandito dalla
lastrina precedente), sono
ben visibili tutte le
componenti (l’angolo A in
corrispondenza dell’astro si
chiama ANGOLO
ALL’ASTRO ma non ha
rilevanza dal punto di vista
nautico):
• la colatitudine (90 – j)
• la distanza polare (p)
• la distanza zenitale (z)
• L’angolo al polo (P)
• L’angolo azimutale (Z)
• L’angolo all’astro (A)
Esempio 1 di sfera celeste
Z
Emisfero SUD
j
• Altezza h = 50°
z
p
• Distanza Zenitale z = 40°
Q
• Angolo Azimutale Z = S 70° E
d
PE
W
h
• Declinazione d = 55°S
• Distanza Polare p = 35°
• Angolo Orario t = 285°
S
Z
• Azimuth Az = 110°
N • Angolo al Polo P = 75°E
Az
E
Q’
Z’
Esempio 2 di sfera celeste
Z
Emisfero SUD
j
p
• Altezza h = 20°
• Distanza Zenitale z = 70°
z
Q
• Azimuth Az = 015°
PE
• Angolo Azimutale Z = S 165° E
d
• Declinazione d = 10°N
W
• Distanza Polare p = 100°
• Angolo Orario t = 345°
h
S
Z
N
• Angolo al Polo P = 15°E
Az
E
Q’
Z’
N.B. La STELLA è nell’emisfero
opposto a quello dell’osservatore
ma è comunque visibile perché
sopra l’orizzonte. Il triangolo di
posizione è molto schiacciato
Esempio 3 di sfera celeste
Z
Emisfero NORD
j
p
• Altezza h = 20°
• Distanza Zenitale z = 70°
z
Q
• Azimuth Az = 195°
PE
• Angolo Azimutale Z = N 165° W
d
• Declinazione d = 10°S
E
• Distanza Polare p = 100°
• Angolo Orario t = 15°
h
N
S
Z
• Angolo al Polo P = 15°W
Az
W
Q’
Z’
N.B. La STELLA è nell’emisfero
opposto a quello dell’osservatore
ma è comunque visibile perché
sopra l’orizzonte. Il triangolo di
posizione è molto schiacciato
Esempio 4 di sfera celeste
Z p
j
z
Emisfero NORD
Az
Astro sul Meridiano
superiore dell’osservatore
d
Q
• Altezza h = 55°
• Distanza Zenitale z = 35°
• Azimuth Az = 180°
h
E
• Angolo Azimutale Z =N 180°E/W
• Declinazione d = 10°N
N
S
Z
• Distanza Polare p = 80°
• Angolo Orario t = 000°
W
Q’
Z’
• Angolo al Polo P = 000°E/W
N.B. La STELLA è sul meridiano
superiore nello stesso emisfero
dell’osservatore. La latitudine in
questo caso si può calcolare
immediatamente j = 90 – h + d
(vedere il disegno)
Esempio 5 di sfera celeste
Z p
j
Emisfero NORD
Az
Astro sul Meridiano
superiore dell’osservatore
z
Q
• Altezza h = 25°
d
• Distanza Zenitale z = 65°
• Azimuth Az = 180°
h
E
• Angolo Azimutale Z =N 180°E/W
• Declinazione d = 10°S
N
S
Z
• Distanza Polare p = 100°
• Angolo Orario t = 000°
W
Q’
Z’
• Angolo al Polo P = 000°E/W
N.B. La STELLA è sul meridiano
superiore nell’emisfero opposto
dell’osservatore. La latitudine in
questo caso si può calcolare
immediatamente j = 90 – h – d
(vedere il disegno)
Esempio 6 di sfera celeste
Z
Emisfero NORD
j
z
p
(
h
Z
(N.B. l’astro dalla parte della
sfera non visibile dal disegnatore
si disegna “tra parentesi”)
)
PE
d
Q
• Altezza h = 30°
• Distanza Zenitale z = 60°
• Azimuth Az = 075°
E
• Angolo Azimutale Z = N 075° E
Az
N
t
S
• Declinazione d = 35°N
• Distanza Polare p = 55°
• Angolo Orario t = 280°
W
Q’
• Angolo al Polo P = 80°E
Ms
PE(A)
Dalle lastrine precedenti sono emerse le relazioni che legano tra
loro le coordinate dello stesso tipo. Di seguito le riassumiamo:
PW(B
)
t(B)
dN
• OSSERVATORE NELL’EMISFERO NORD
• ASTRO AD EST
A
• PE = 360°- t
Z
dN
p
p
B
E
Pn
W
• Z = N Az E
• ASTRO AD OVEST
N
• PW = t
• Z = N (360 – Az) W
t(A)
Mi
Punto di osservazione della
sfera celeste: sopra lo Zenit
S
AZ(B)
Ms
Z
E
h
A
W
z
z
B h
Pn
AZ(A)
Z(A)
N
Z(B)
ASTRO A
ASTRO B
h = 55°
h = 38°
z = 35°
z = 52°
Az = 090°
Az = 285°
Z = N 90°E
Z = N 75°W
ASTRO A
ASTRO B
d = 44°N
d = 25°N
p = 46°
p = 65°
t = 295°
t = 80°
P = 65°E
P = 80°W
Punto di osservazione della sfera
celeste: sopra il Polo Nord
RELAZIONI TRA LE COORDINATE
Ms
PW(A
Dalle lastrine precedenti sono emerse le relazioni che legano tra
loro le coordinate dello stesso tipo. Di seguito le riassumiamo:
PE(B)
t(A)
)
dS
• OSSERVATORE NELL’EMISFERO SUD
• ASTRO AD EST
A
• PE = 360°- t
Z
dS
p
p
B
W
Ps
E
• Z = S (180-Az) E
• ASTRO AD OVEST
• PW = t
t(B)
S
• Z = S (Az - 180) W
Mi
Punto di osservazione della
sfera celeste: sopra lo Zenit
N
AZ(B)
Ms
W
Z
h
A
E
z
z
B h
Ps
Z(A)
AZ(A)
S
Z(B)
ASTRO A
ASTRO B
h = 55°
h = 38°
z = 35°
z = 52°
Az = 270°
Az = 105°
Z = S 90°W Z = S 75°E
ASTRO A
ASTRO B
d = 44°S
d = 25°S
p = 46°
p = 65°
t = 65°
t = 280°
P = 65°W
P = 80°E
Punto di osservazione della sfera
celeste: sopra il Polo Nord
RELAZIONI TRA LE COORDINATE