PPT

Decadimento b
Decadimento b
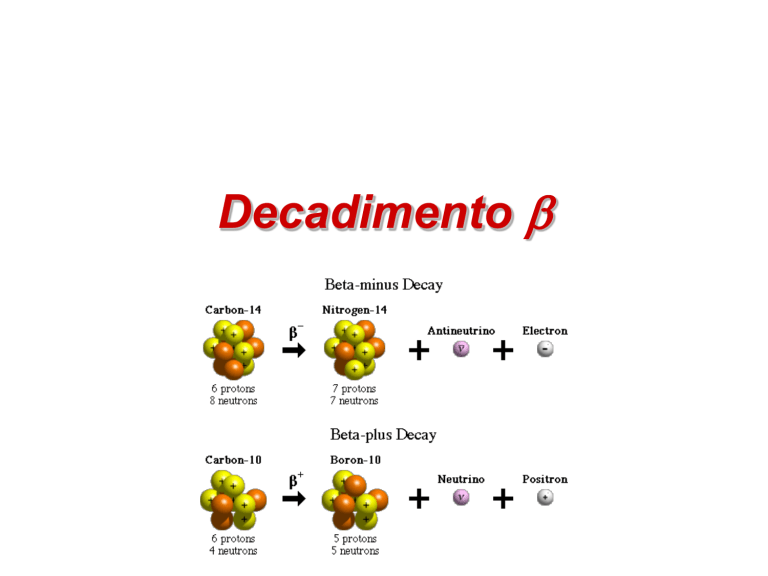
Decadimento b-:
 Nuclei che nel piano N-Z hanno un
eccesso di neutroni rispetto a
quanto previsto dalla curva di
stabilità, tendono a “trasformare”
un neutone in un protone
( Z , A)  ( Z  1, A)  e   e
Decadimento b+:
 Nuclei che nel piano N-Z hanno un
eccesso di protoni rispetto a
quanto previsto dalla curva di
stabilità, tendono a “trasformare”
un protone in un neutrone
( Z , A)  ( Z  1, A)  e   e
2
Cattura elettronica
Un nucleo ricco di protoni può catturare un elettrone
atomico e trasformare un protone in un neutrone
 Stesso effetto di un decadimento b+
 L’elettrone viene tipicamente catturato dalla shell K che è
caratterizzata da una funzione d’onda sensibilmente diversa da
zero nel volume del nucleo
e   ( Z , A)  ( Z  1, A)   e
Nota:
 La cattura elettronica ha un Q-valore più alto del decadimento b+
e quindi più energia cinetica a disposizione delle particelle nello
stato finale
 Ci sono casi in cui la differenza di massa tra (Z,A) e (Z-1,A) è
troppo piccola (<1.022 MeV) per consentire il decadimento b+, ma
la cattura elettronica può invece avvenire, ad esempio: 83Rb
decade in 83Kr (DM = 0.9 MeV) solo attraverso cattura elettronica 3
Dal modello a goccia (1)
Dalla formula della massa di un nucleo, per A fissato si
vede una dipendenza parabolica da Z:
M ( A, Z )  ZM p  ( A  Z ) M n  aV A  aS A
2/3
Z2
( A  2Z ) 2
 aC 1/ 3  a A
 A1/ 2
A
A
4a 
 a
M ( A, Z )  Z 2  1C/ 3  A   Z ( M p  M n  4a A )  A( M n  aV  a A )  aS A2 / 3  A1/ 2
A 
A
 che ha un minimo per:
Z0 
 ( M p  M n  4a A ) 4a A  M n  M p
A 4a A  M n  M p


2/3
2
2
a
A
 4a A
 aC 4a A 
2/3
C
a
A

4
a
2 1/ 3 

C
A
A
A
A





A  1  M n  M p / 4a A  A 
1.014
  

Z 0  
2/3 
2/3 
2  1  aC / 4a A  A
 2  1  0.0076 A 
4
Dal modello a goccia (2)
Nuclei con A dispari:
 Il parametro  vale 0 e quindi M(A,Z) ha un solo valore
 Fissato A esiste un solo isobaro stabile con Z=Z0
5
Dal modello a goccia (3)
Nuclei con A pari
 M(A,Z) assume due valori diversi per nuclei pari-pari e dispari-dispari
 Possono esserci fino a 3 isobari stabili per i nuclei pari-pari
 Tutti i nuclei dispari-dispari devono essere instabili
 Uniche eccezioni sono: 2H, 6Li, 10B e 14N in cui le parabole sono disposte come in
figura b)
nuclei
dispari-dispari
nuclei
pari-pari
6
Dal modello a goccia (4)
Nuclei con A pari
 Caso particolare in cui A=14 -> stato stabile dispari-dispari
7
Teoria elementare di Fermi
Modello del 1934 basato sulla teoria di Fermi delle interazioni
deboli
 Si usa la seconda regola d’oro di Fermi per calcolare il rate di
decadimento:
2
2
w
  f | H int | i   ( E f )

Ipotesi:
 La hamiltoniana di interazione è un operatore che agisce sui campi
fermionici mediante assorbimento o emissione di fermioni
 L’interazione è a corto raggio d’azione (interazione a contatto)
 Spiegato nella teoria elettro-debole dall’alto valore di massa dei mesoni W che
mediano l’interazione debole
8
Densità degli stati finali (1)
Il termine di densità degli stati finali determina la forma
dello spettro beta, cioè la distribuzione delle energie degli
elettroni (positroni) emessi
 Il numero di stati in cui l’elettrone ha quantità di moto compresa
nell’intervallo tra pe e pe+dpe e il neutrino nell’intervallo compreso
tra pν e dpv è dato da:
 4 pe2 dpe   4 p2 dp  16 2V 2 2
2
d N  dN e dN  V
V

p
dp
p
dp
e
e



3
3
6
h
h


 (2)
2
 Integrato su tutte le possibili direzioni della quantita’ di moto ( ∫dW=4 )
 Integrato su tutte le possibili coordinate all’interno del volume di
normalizzazione ( ∫d3x=V )
 Il volume della celletta di quantizzazione vale h3
9
Densità degli stati finali (2)
Si introduce l’energia Ef a disposizione nello stato finale:
E f  M ( Z , A)  M ( Z  1, A)c2  TZ 1, A  Ee  E  Ee  E
 dove si è trascurata l’energia cinetica di rinculo del nucleo
Gli impulsi di elettrone e neutrino sono legati dalla
conservazione dell’energia
 Per Ee fissato: si esprime p in fuzione di Ef
E f  Ee  p2c 2  m2c 4
p2c 2  E f  Ee   m2c 4
2
1
p 
c
E
 Ee   m c
2
f
2 4
p dp

E

f
 Ee 
dE f
2
c
10
Densità degli stati finali (2)
Il termine di densità degli stati finali determina la forma dello
spettro beta, cioè la distribuzione delle energie degli elettroni
(positroni) emessi
 4 pe2 dpe   4 p2 dp  16 2V 2 2
2
d N  dN e dN  V
V

p
dp
p
dp
e
e



3
3
6
h
h


 (2)
2
 Sostituendo
1
p 
c
E
 Ee   m c
2
f
2 4
p dp

E

f
 Ee 
dE f
2
c
 Si ricava:
2 2
16

V 2 1
2
2
2 4


d N
p
E

E
(
E

E
)

m
e 3
f
e
f
e
 c dE f dpe
6
(2)
c
11
Densità degli stati finali (3)
La densità degli stati finali per i quali l’elettrone ha una
quantità di moto compresa tra pe e pe+dpe è quindi:
d 2N
16 2V 2 1
2
2 4 2


 ( E f )dpe 
dpe 
E

E
(
E

E
)

m
f
e
f
e
 c pe dpe
6
3
dE f dpe
(2) c
che in caso di massa nulla del neutrino si riduce a:
d 2N
16 2V 2 1
2 2
 ( E f )dpe 
dpe 
(
E

E
)
pe dpe
f
e
6
3
dE f dpe
(2 ) c
m=0
End point:
Ef=Ee
pmax=√(Ef2-me2c4)
m>0
12
Campo coulombiano del nucleo
Deformazione dello spettro beta dovuta all’interazione
dell'elettrone (positrone) con il campo coulombiano del nucleo.
 L'effetto è diverso per il decadimento b-, in cui il potenziale è
attrattivo, e per il decadimento b+, in cui il potenziale è repulsivo
La distribuzione di momento degli elettroni (positroni) diventa:
dN 16 2V 2 1
2
2 4
2



E

E
(
E

E
)

m
c

p
f
e
f
e

e  F ( Z D , Ee )
6
3
dpe (2) c
 F(ZD,Ee) è la funzione di Fermi che è stata calcolata e tabulata ed è
apprezzabilmente diversa da 1 solo per ZD (numero di protoni nel nucleo
figlio) grandi o energie piccole
13
Grafico di Fermi-Kurie (1)
Se si riscrive la distribuzione di momento degli elettroni emessi
come:
1 dN
2
2 4



costante

E

E
(
E

E
)

m
f
e
f
e
 c  F ( Z D , Ee )
2
pe dpe
Nel caso di massa nulla del neutrino si ha:
1 dN / dpe
 costante  E f  Ee 
2
pe F ( Z D , Ee )
 che mostra una dipendenza lineare da Ee
 La retta, in caso di massa nulla del neutrino interseca l’asse x nel punto
Ee=Ef
Questo modo di presentare i dati sperimentali è il grafico di
Fermi-Kurie
 La conferma sperimentale dell'andamento previsto costituisce il primo
successo della teoria di Fermi.
14
Grafico di Fermi-Kurie (2)
3
H 3He  e   e
La misura della distribuzione vicino all’end-point (Emax)
della distribuzione, fornisce un metodo per misurare la
massa del neutrino.
 La misura più precisa è stata fatta studiando il decadimento del
Trizio:
3
H 3He  e   e
 Nuclei semplici, correzioni facili da valutare
 Energia disponibile nello stato finale è piccola (530 keV) -> aumenta la
sensibilità della misura
15
Elemento di matrice (1)
Elemento di matrice per un decadimento b:

 * 
   
  f | H int |  i   *f H int i dV   e* (re ) * (r ) Nf
(r ) H int Ni (r )dre dr dr
 Ni è la funzione d’onda che descrive il nucleone “genitore” all’interno del
nucleo prima del decadimento
 e e n sono le funzioni d’onda dell’elettrone e del neutrino
 Nf è la funzione d’onda che descrive il nucleone “figlio” all’interno del nucleo
dopo il decadimento
 L’integrale è esteso al volume del nucleo
Nella teoria di Fermi si fa l’ipotesi che l’interazione avvenga
“a contatto”, per cui l’hamiltoniana di interazione vale:
 
 
H int  g (re  r )  (r  r )
 dove g è la costante di accoppiamento che ha dimensioni [energia x
volume] e misura l’intensità dell’interazione
 L’elemento di matrice risulta quindi:
 *  * 
 
  f | H int |  i  g  (r )  (r ) Nf (r ) Ni (r )dr
*
e
16
Elemento di matrice (2)
Dall’ipotesi di raggio d’azione nullo per Hint, segue che
elettrone e neutrino sono particelle in moto libero dopo il
decadimento
i  
i  


1  p r
1  p r
 e (r ) 
e
  (r ) 
e
e
V
V
 Si trascura l’interazione coulombiana dell’elettrone con il nucleo,
che è stata inclusa nel fattore di Fermi
 Il volume di integrazione (il nucleo) ha un raggio di qualche fermi e
le energie dell’elettrone sono dell’ordine del MeV, quindi pr<<1 e si
può approssimare:
e
i  
pe  r

i  
 1  pe  r  ...  1

 Quindi, al primo ordine, l’elemento di matrice si riduce all’integrale
delle funzioni d’onda dei nucleoni coinvolti nel decadimento:

  g
g
*
  f | H int |  i   Nf (r ) Ni (r )dr  M if
V
V
17
Rate di decadimento
La probabilità di transizione per unità di tempo per
emissione di elettroni con quantità di moto compresa tra pe
e pe+dpe dalla seconda regola d’oro di Fermi vale quindi:
2 2
2 16 V
2 g 2
1
2
2 4
2


dw 
M

E

E
(
E

E
)

m
c
F
(
Z
,
E
)
p
if
f
e
f
e

D
e
e dpe
2
6
3
 V
(2) c
2
g2
dw  3 7 3 M if  F ( Z D , Ee )  E f  Ee  ( E f  Ee )2  m2c 4 pe2dpe
2  c
 che in caso di massa del neutrino nulla o trascurabile diventa:
2
g2
2
dw  3 7 3 M if  F ( Z D , Ee )  E f  Ee  pe2dpe
2  c
18
Vita media (1)
La vita media è data da:
pmax
1
  dw

0
 dove 0 - pmax è il range di impulso dell’elettrone nello stato finale
g2
 3 7 3 M if
 2  c
1
2

pmax
0
F ( Z D , Ee )  E f  Ee  pe2 dpe
2
 Per calcolare l’integrale conviene introdurre le variabili:
  mEc
e
 da cui:

2
2

  2 1
p
me c
E f  Emax  me c 2 0
pmax 
 e quindi:
E
 Ee  pe2 dpe  me c 2 0  me c 2  (me c)3 2 d  me5c 7 ( 02   2  2 0 ) 2 d 
2
2
f
1
2
Emax
 me2 c 4  me c0
c


 me5c 7 2   02   2  2 1   02 1   2  2 d
19
Vita media (2)
L’integrale che compare nella formula della vita media
dipende solo dal limite superiore di integrazione pmax, o 0
 Si pone:
0


f (Z D ,0 )   F (Z D , )  2  02   2  2 1  02 1   2  2 d
0
 E quindi:
2
g2
 3 7 3 M if me5c 7 f ( Z D ,0 )
 2  c
1
(me c 2 )5
2
 3
g
M if
6
 2  (c)
1
2
f ( Z D ,0 )
La vita media risulta essere il prodotto di:
 Una costante (mec2)5/23ħ(ħc)6 = 1.46104 MeV-2fm-6s-1
 Il quadrato della costante di accoppiamento, dimensioni: MeV2fm6
 Il quadrato dell’elemento di matrice adimensionale Mif
 La funzione adimensionale f(ZD,0) che dipende dalla carica del
nucleo e del limite superiore di integrazione 0=pmax/mec
20
Costante di accoppiamento
Il rapporto G=g/(ħc)3 è la costante di Fermi che ha le
dimensioni di [Energia-2]
 Dal decadimento beta del neutrone si misura:
g
-5
2


GF 

1
.
140

0
.
002

10
GeV
(c)3
b
 Dalla misura della vita media del muone si ricava:
G F  1.16639  0.00001105 GeV 2
 che è detta costante universale di Fermi
Si conclude che l’accopiamento del campo debole con i
leptoni non è esattamente uguale a quello con i quark
 L’origine di questa differenza è dovuta al mixing dei sapori dei
quark attraverso l’angolo di Cabibbo
 L’accoppiamento debole tra quark u e d vale gcos C
G Fb  G F cos C
21
f(ZD,0)
I valori della funzione f(ZD,0) sono stati calcolati e
tabulati
 Risulta molto sensibile all’energia dell’end-point
22
Legge di Sargent
In decadimenti in cui l’energia disponibile Ef è >> mec2, si ha:
0=pmax/mec>>1 e F(Z,)≈1.
 Si può quindi approssimare:
0
f ( Z D ,0 )  
0
0

0
 2 
 
2
0
2
2
0

0
  2  2 1  02 1   2  2 d  
   20
4
3
 d  
2
0

0
3 0
3

0

5 0
5


  2  2 02  2  2 d 
2
0
 20

0
4 0
4
0
5
 1 1 1  5 0
    0 
30
3 5 2
 E quindi (essendo pmaxc ≈ Emax=Ef):
5
2
(me c 2 )5
( pmax c)5
2
2
0
 3
g
M

g
M if
if
6
3
6
 2  (c)
30 60  (c)
1
2
1


E 5f
60  (c)
3
2
6
g M if
2
Questa approssimazione ci dà la legge di Sargent che dice
che la vita media è inversamente proporzionale alla quinta
potenza dell’energia a disposizione nello stato finale
 Questo è uno dei motivi alla base delle diverse vite medie dei
decadimenti b dei nuclei
23
Legge di Sargent
Legge di Sargent che dice che la vita media è
inversamente proporzionale alla quinta potenza dell’energia
a disposizione nello stato finale
1


E 5f
60 3 (c) 6
g 2 M if
2
24
Valore di log-ft
Si possono usare le misure della vita media dei nuclei per
ricavare il valore di g|Mif| che contiene l’informazione sulla
struttura nucleare
E’ conveniente introdurre il valore ft (ft-value) definito come
il prodotto di f(Z,0) e del tempo di dimezzamento t1/2=ln2
ft  value  f ( Z D ,0 )  t1/ 2
2 3 (c)6
1

(me c 2 )5 g 2 M
if
2

costante
2
g M if
2
 Può essere interpretato come la
vita media corretta per gli
effetti nucleari (Z) e per
l’energia a disposizione (0)
 Il valore di ft varia tra un minimo
di 103 s e un massimo di 1022 s,
per cui di solito si usa il log-ft
value che è il logaritmo il base 10
del ft-value
25
Momento angolare
Conservazione del momento angolare nel decadimento beta:


 
JP  JD  L  S
 JP e JD sono lo spin dei nuclei genitore e figlio, L (=Le+L) il momento angolare
orbitale dei leptoni, e S (=Se+S) lo spin dei leptoni
Un ragionamento semiclassico ci dice che il momento angolare orbitale
dell’elettrone e del neutrino è dato da:
L   (  1)  pb  pR
 dove b è il parametro di impatto e R il raggio del nucleo
 Si ricava:
(  1) 
pe R
 10  2  1

 0
 dato che R è dell’ordine di qualche fm e pe è al più dell’ordine di qualche MeV/c
I decadimenti con l=0 si chiamano permessi, quelli con l>0 proibiti
I leptoni sono emessi preferenzialmente senza momento angolare
orbitale
 La somma degli spin dei leptoni deve bilanciare la variazione di momento
angolare del nucleo
26
Spin nel decadimento beta
Gli spin dell’elettrone (positrone) e del neutrino possono
essere paralleli o anti-paralleli.
Spin di e antiparalleli  (S=0)
-> transizioni di Fermi
 Elettrone e neutrino sono in uno
stato di singoletto
Spin di e paralleli   (S=1)
-> transizioni di Gamow-Teller
 Elettrone e neutrino sono in uno
stato di tripletto
Entrambi i tipi di transizione possono avvenire
Un singolo decadimento beta può essere una mistura dei
due tipi di transizione
27
Transizioni permesse e proibite
I decadimenti con l=0 si chiamano permessi, quelli con l>0 proibiti
 NOTA: questa non è un vera e propria regola di selezione: decadimenti
l
con >0 sono possibili, anche se improbabili
Le funzioni d’onda dell’elettrone e del neutrino:
i 

1  p r
1
 e, (r ) 
e

V
V
 i  

1

p

r

...
 

 possono essere viste come uno sviluppo in serie nel numero quantico l
 Il prodotto pr/ħ è dell’ordine di 10-2: i termini della successione
diventano via via più piccoli
Il valore log-ft dipende dal modulo quadrato di Mif, quindi ogni
unità di l porta un fattore di soppressione del rate di
decadimento dell’ordine di 10-3-10-4
 Il primo termine della serie (=il valore di l più basso) che rispetta la
conservazione del momento angolare domina in Mif e quindi determina il
valore di log-ft e il rate di transizione
28
Parità
Per transizioni permesse (l=0) la parità del nucleo deve
rimanere immutata, visto che Pf=Pi (-1)l
 L’elemento di matrice al prim’ordine si annulla se la parità del nucleo
cambia

 
*
M if 0   Nf
(r ) Ni (r )dr  0 se P f  P i
Transizioni in cui cambia la parità del nucleo devono essere
quindi descritte dai termini successivi dello sviluppo:
M if 0 
  
  1
   2
 
i
*
*

(
r
)
p

r

(
r
)
d
r


(
r
)(
p

r
)

(
r
)dr  ...
Nf
Ni
Ni
2  Nf


2
 Il primo termine corrisponde a transizioni con l=1 e cambio di parità
-> decadimenti primo-probiti (first-forbidden)
 Soppresse di un fattore 10-4  vita media più lunga di un fattore 104
 Il termine successivo corrisponde a transizioni con l=2 senza cambio
di parità -> decadimenti doppio-probiti (double-forbidden)
29
Regole di selezione
Le regole che mettono in relazione le caratteristiche del
decadimento (=variazione di momento angolare e parità
del nucleo) con l’ordine della transizione (permessa, primo
proibita …) si chiamano regole di selezione
 La transizione con il valore di l più basso che non viola le regole di
selezione determina il rate di decadimento e il valore di log-ft
30
Transizioni permesse
Transizioni permesse:
 Il momento angolare orbitale della coppia elettrone-neutrino è 0, lo
spin è 1/2, quindi il momento angolare totale portato via della coppia
elettrone neutrino può essere J=0 o J=1
 Quindi nei decadimenti beta permessi, la variazione di momento
angolare tra nucleo padre e figlio sarà DJ=0 o DJ=1
Transizioni permesse di Fermi (S=0, ):
 Le transizioni permesse lasciano immutati il momento angolare e la
parità del nucleo
DJ  0 DP  No
Transizioni permesse di Gamow-Teller (S=1,  ):
 Le transizioni beta permesse lasciano immutata la parità del nucleo,
ma c’è un cambio di momento angolare:
DJ  0, 1 (ma non 0  0)
DP  No
 Il caso 00 è escluso perché non c’è momento angolare da portare via
31
Esempi di transizioni permesse
Pura transizione di Gamow-Teller
Pura transizione di Fermi
Transizioni miste (DJ=0, ma Ji0)
Il rate di decadimento e l'elemento
di matrice Mif dipendono da:
• overlap dalle funzioni d’onda dei
nucleoni nel nucleo.
• principio di esclusione di Pauli
che impedisce che il nuovo
nucleone vada in uno stato già
occupato
32
Transizioni super-permesse
Transizioni super-permesse:
 Se le funzioni d’onda nel nucleo dei nucleoni genitore e figlio si
″sovrappongono″ perfettamente, il probabilità di decadimento è grande
 Caso in cui il protone e il neutrone coinvolti nel decadimento hanno gli stessi numeri
quantici
 I valori ft per questo tipo di decadimento sono simili a quelli del decadimento del
neutrone libero
 Sono tipicamente decadimenti b+ (eccezione il decadimento del 3H in
3He)
 La repulsione Coulombiana nel nucleo separa leggermente i livelli energetici dello
stesso multipletto di isospin, con energie più elevate per stati con più protoni e meno
neutroni
Esempio:
14O
14N
p
p
n
n
b
1p1/2
1p1/2
1p3/2
1p3/2
1s1/2
14O
1s1/2
14N
33
Permesse e super-permesse
Distribuzioni di log-ft (logf dalla teoria + logt1/2 misurato)
per transizioni permesse e super-permesse:
 La larghezza della distribuzione di log-ft all’interno di una classe
è dovuta alla variazione dell’elemento di matrice Mif
 Esempio: 14C14N (transizione permessa di Gamow-Teller pura)
 t1/2=5730 anni
 log-ft = 9.04 ( >> dei valori tipici dei decadimenti permessi )
34
Transizioni proibite
La transizione con il valore di l più basso che non viola le regole
di selezione determina il rate di decadimento e il valore di log-ft
l
Per transizioni proibite ( >0) l’elemento di matrice Mif dipende
dal momento dell’elettrone
 Ha effetto anche sulla forma dello spettro dell’elettrone emesso
 Un grafico di Fermi-Kurie non-lineare è un’indicazione che una certa
transizione è di tipo proibito
35
Transizioni primo-proibite
Transizioni primo-proibite:
 Elettrone e neutrino possono essere emessi con spin totale S = 0
oppure S = 1
 La conservazione del momento angolare, DJ = L+S, produce le regole
di selezione per le transizioni proibite al primo ordine
Transizioni primo-proibite di Fermi (S=0, ):
DJ  0,1 ( ma non 0  0) DP  Si
Transizioni primo-proibite di Gamow-Teller (S=1,  ):
DJ  0, 1, 2
DP  Si
36
Esempi di transizioni proibite
p
n
1f7/2
p
n
b
b
 1d3/2
p
1f7/2
1f7/2
1d3/2
1d3/2
n
40K
40Ar
40K
40Ca
: t1/2 = 1.27109 anni,f=1018s
 I nucleoni “un-paired” nel 40K si sommano a JP=4-, mentre gli stati
base del 40Ar e 40Ca sono 0+ -> decadimento triplo-probito
 Il decadimento nel più basso stato eccitato del 40Ar (JP=2+) per
cattura elettronica è primo proibito, ma lo spazio delle fasi è molto
piccolo perché il Q-valore è di soli 0.049 MeV
137Cs
137Ba : DJ=2, f = 4109 s
37
Appendice: angolo di
Cabibbo

Decadimenti
deboli


n
p
L0
p
Diagrammi a livello
di Quark
n
d
p
L0
p
Decadimenti leptonici: l’interazione debole cariche fanno passare da un componente
del doppietto a un altro, ma mai da un doppietto a un altro (-> conservazione del
numero leptonico)
Decadimenti adronici: si osservano anche transizioni fra quark di diversi doppietti:
da quark s a quark u (processi con variazione di stranezza)
 Sperimentalmente, si osserva sempre che l’intensità dell’accoppiamento (G) delle transizioni
adroniche con variazione nulla di stranezza è solo il 2% più piccola di quelle leptoniche, mentre le
transizioni adroniche con violazione di stranezza hanno accoppiamento tipicamente circa 5 volte
minore
39
Angolo di Cabibbo
Soluzione di Cabibbo (1963): gli autostati della massa (che
sono anche gli autostati dell’interazione forte, non sono
anche autostati dell’interazione debole
 NOTA: sperimentalmente si osservano particelle con massa e vita
media definite, cioè gli autostati della massa
Posposta di Cabibbo: l’autostato dell’interazione debole è
una combinazione degli autostati della massa
d '  d cosC  s sin C
Si può definire un doppietto di isospin debole come:
u

u 


   
 d '   d cosC  s sin C 
 Il bosone W accoppia lo stato d’ con il quark u
40
Decadimenti deboli


n
d
p
L0
p
Introducendo l’angolo di Cabibbo:
Da cui:
L0  p e   e 
2

tan
C

n  p e  e 
C  13
41
Costante universale di Fermi
Dal decadimento beta del neutrone si misura:
g
-5
2


GF 

1
.
140

0
.
002

10
GeV
(c)3
b
Dalla misura della vita media del muone si ricava:
G F  1.16639  0.00001105 GeV 2
 che è detta costante universale di Fermi
Si conclude che l’accopiamento del campo debole con i
leptoni non è esattamente uguale a quello con i quark
 Non universalità dell’interazione debole?
 NO! L’interazione debole è universale!
L’origine di questa differenza è dovuta al mixing dei sapori
dei quark attraverso l’angolo di Cabibbo
 L’accoppiamento debole tra quark u e d vale gcos C
G Fb  G F cos C
42