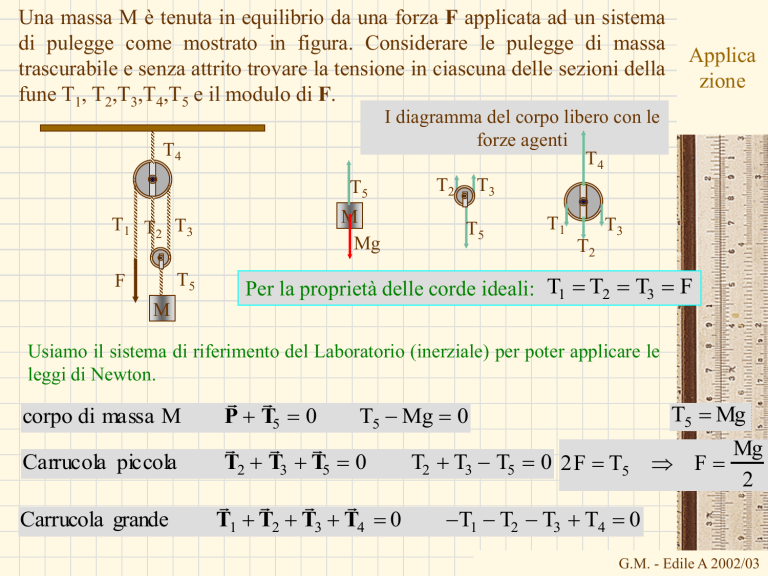
Una massa M è tenuta in equilibrio da una forza F applicata ad un sistema
di pulegge come mostrato in figura. Considerare le pulegge di massa
trascurabile e senza attrito trovare la tensione in ciascuna delle sezioni della
fune T1, T2,T3,T4,T5 e il modulo di F.
T4
T5
T5
F
M
I diagramma del corpo libero con le
forze agenti
T4
T2 T3
M
Mg
T1 T2 T3
Applica
zione
T5
T1
T2
T3
Per la proprietà delle corde ideali: T1 T2 T3 F
Usiamo il sistema di riferimento del Laboratorio (inerziale) per poter applicare le
leggi di Newton.
corpo di massa M
P T5 0
Carrucola piccola
T2 T3 T5 0
Carrucola grande
T5 Mg
T5 Mg 0
T1 T2 T3 T4 0
T2 T3 T5 0 2F T5
Mg
F
2
T1 T2 T3 T4 0
G.M. - Edile A 2002/03
T4
T5
M
Mg
T1 T2 T3
T5
F
M
I diagramma del corpo libero con le
forze agenti
T4
T2 T3
T5
T2
T3
Per la proprietà delle corde ideali: T1 T2 T3 F
corpo di massa M
P T5 0
Carrucola piccola
T2 T3 T5 0
T5 Mg
T5 Mg 0
T2 T3 T5 0
2F T5
Carrucola grande
T1
Applica
zione
T1 T2 T3 T4 0
F
Mg
2
T1 T2 T3 T4 0
T4 3F
T4
3Mg
2
G.M. - Edile A 2002/03
T4
T5
T1 T2 T3
M
Mg
I diagramma del corpo libero con le
forze agenti
T4
T2 T3
T5
T1
T2
Applica
zione
T3
T5
F
M
N.B.: Quando si ha a che fare con carrucole e corde, la tensione della
corda va pensata applicata alla carrucola nel punto di tangenza della corda
alla carrucola.
Infatti uno può pensare che la parte di corda a contatto della carrucola sia
un tutt’uno con la carrucola stessa (la corda non scorre sulla carrucola): ne
deriva che il punto di attacco della corda alla carrucola è proprio il punto
di tangenza.
G.M. - Edile A 2002/03
Due molle di costante elastica k1=104 N/m e k2=2x104 N/m,
rispettivamente, sono collegate come in figura. Una estremità di ciascuna
Applica
molla è fissato al soffitto mentre le altre sono vincolate ad un corpo di
zione
massa m=10kg. Si calcoli l’allungamento delle due molle quando il corpo è
in equilibrio.
y
Fel1
Fel2
m
O
P
m
G.M. - Edile A 2002/03
Due molle di costante elastica k1=104 N/m e k2=2x104 N/m,
rispettivamente, sono collegate come in figura. L’estremità superiore della
Applica
prima molla è fissato al soffitto mentre l’estremità inferiore è vincolata ad
zione
un corpo di massa m=10kg. Si calcoli l’allungamento di ciascuna molla e
quello complessivo quando il corpo è in equilibrio.
y
F1s
Molla 1
F21
Molla 2
F12
F2m
Fm2
Molla 1
P
Molla 2
m
m
F1s = forza sulla molla 1 dovuta al soffitto
F12 = forza sulla molla 1 dovuta alla molla 2 (il modulo F12=k2Dy2)
F21 = forza sulla molla 2 dovuta alla molla 1 (il modulo F21=k1Dy1)
F2m = forza sulla molla 2 dovuta al corpo di massa m
Fm2 = forza sul corpo di massa m dovuta alla molla 2
F12 =- F21
F2m =- Fm2
G.M. - Edile A 2002/03
Due blocchi (m=1.0 kg e M = 10 kg) e una molla (k=200 N/m) sono
sistemati come in figura su una superficie orizzontale priva di attrito. Il
coefficiente di attrito statico tra i due blocchi è 0.40. Qual è la massima
ampiezza del moto armonico semplice per evitare lo slittamento dei due
blocchi. Se l'ampiezza del moto è più piccola di quella massima quanto
vale il periodo?
Scrivere infine l'espressione (in funzione del tempo) della componente
verticale e di quella orizzontale della reazione vincolare esercitata dal
blocco di massa M su quello di massa m.
Applica
zione
Vedi il problema precedente: sostituire la forza F con
la forza elastica!
k
m
M
G.M. - Edile A 2002/03
Due masse, connesse da una corda ideale e priva di massa, passante su di
una carrucola assimilabile ad un disco, partono da ferme dalla posizione
illustrata in figura. Qual è la loro velocità relativa quando passano l’una di
fronte all’altra (stessa quota)?
Quanto tempo impiegano i due corpi per raggiungere questa
configurazione?
T1
Applica
zione
T2
P1
P2
T1= T2 =T
G.M. - Edile A 2002/03
Una lampada è sospesa ad un filo nella cabina di un ascensore. Si supponga
che la cabina stia salendo e, per fermarsi al piano, rallenta con una
accelerazione di modulo 2.4 m/s2. Se la tensione nel filo che sostiene la
lampada è di 89 N, qual è la massa della lampada?
Quale sarà la tensione nel filo quando l'ascensore riparte con una
accelerazione di pari modulo, 2.4 m/s2, per raggiungere un piano più in
alto?
T
P
Applica
zione
a
v
G.M. - Edile A 2002/03
Una palla viene lanciata contro un muro con la velocità iniziale di 25.0 m/s
a un angolo di 40° rispetto al suolo orizzontale come mostrato in figura. Il
muro si trova a 22 m dal punto di lancio.
Trascurando la resistenza dell’aria determinare:
• quanto tempo la palla rimane in aria prima di colpire la parete.
• quali sono le componenti orizzontale e verticale della velocità
all’istante in cui la palla colpisce la parete
• se nel momento in cui tocca la parete ha già superato il vertice della
traiettoria.
Applica
zione
G.M. - Edile A 2002/03
Un treno di massa 5x105 Kg sta viaggiando orizzontalmente a 60
km/h e sta effettuando una curva il cui raggio di curvatura è 1
km. Allo stesso tempo sta decelerando ed il tasso di decrescita
(accelerazione) del modulo della velocità è di 0.1 m/s2. La
lunghezza del treno è trascurabile confrontata con le dimensioni
della curva ed il treno può essere trattato come un punto. Che
forza totale esercitano i binari sul treno? (dare la risposta
all'inizio della curva, quando cioè la velocità può essere
considerata ancora uguale a 60 km/h).
Applica
zione
R=1 km
ut
un
G.M. - Edile A 2002/03
Due blocchi, di massa m1=2.3 kg e m2=1.2 kg, sono poggiati su un
piano orizzontale privo di attrito come mostrato in figura. Se al
corpo di massa m1 viene applicata una forza di intensità pari a
F=3.2 N, determinare l'accelerazione dei due blocchi e la forza di
contatto tra i due. Determinare le stesse quantità nel caso in cui
la forza F viene applicata al blocco di massa m2 e confrontarle con
quelle determinate precedentemente. Spiegare le eventuali
differenze.
m1
F
Applica
zione
m1
m2
m2
F
N1
F
m1
N12
P1
N2
N21 m2
P2
G.M. - Edile A 2002/03
Nella figura A e B sono due blocchi rispettivamente di 4.4 kg e
2.6 kg. I coefficienti di attrito statico e dinamico tra il blocco A e il
piano sono rispettivamente 0,18 e 0,15.
• Si determini la minima massa del corpo C che impedisce ad
A di scivolare.
• Improvvisamente il blocco C viene tolto da A. Valutare
l'accelerazione di A e la tensione nella corda.
NCA
C
N
A
NAC
C
A
C
PC
TA
Applica
zione
B
TB
B
PA
PB
G.M. - Edile A 2002/03












