spettrografi-e-rivelatori - Dipartimento di Fisica e Astronomia

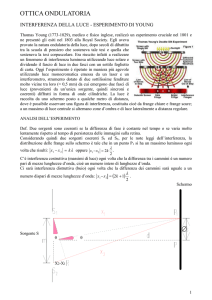
Diffrazione da una fenditura

sin 2 x
y
x2
d

x

d sin 

Fronti d’onda
piani
y  0  x   ,  2 , ..., m  d sin   m
Disco di Airy
θ  1.22
Fenditura circolare
λ
d
θ  2.33
λ
d
Potere risolutivo teorico del telescopio
D
θ
θ
Esempio: D=10m, =5500 Å  =0.014”
D=10m, =5 cm  =21’
1.22
λ
D
Interferenza fra due fenditure

sin 2 x
s 
y  2 cos 2  x 
x
d 
d
s
d

x  d sin 

Fronti d’onda
piani
s  3d
Interferenza fra due fenditure

sin 2 x
s 
y  2 cos 2  x 
x
d 
d
s
d
Fronti d’onda
piani
s  6d

x  d sin 

Keck I e II (Hawaii)
Very Large Array (VLA, New Mexico)
Interferenza fra N fenditure
s 
2
sin
N
x

sin 2 x
 d 
y
x2

2 s
sin  x 
d 

s
d


x  d sin 

Fronti d’onda
piani
s  2d
N  10
d sin   m
Lo spettro
s  2d
N  25
Riga spettrale
 = 4400 Å
m=0
d sin   m
Riga spettrale
 = 4400 Å
m=1
d sin   m
 = 4400 Å
 = 4400 Å
m=0
m=1
d sin   m
 = 4400 Å= 5500 Å
 = 4400 Å
 = 5500 Å
m=0
m=1
d sin   m
 = 4400 Å= 5500 Å= 6500 Å
 = 4400 Å
 = 5500 Å
 = 6500 Å
m=0
m=1
-1
0
1
Equazione del reticolo
Angolo di
diffrazione
Lunghezza
d’onda
sin r m 
Ordine
Densità di tratti del
reticolo
Idrogeno
Ferro

Schema di uno spettrografo
telescopio
fenditura
reticolo
lente di
camera
rivelatore
collimatore
I Rivelatori
OCCHIO
Legge psico-fisica di Weber-Fechner:
un incremento percentuale dell’intensità luminosa (I)
produce un incremento lineare dello stimolo visivo (s)
s  k 
I
I
 s  log I
Fino agli anni ‘80: lastre fotografiche
Effetto  annerimento dell’emulsione o densità (D)
Causa  esposizione (E) ad un flusso di radiazione
incidente (I) per un certo tempo (t)
D
Log E
Dalla fine degli anni ‘80: CCD (Charged Coupled Device)
Vantaggi dei CCD:
• Maggiore sensibilità
• Linearità
• Immagini digitali
Come funziona un CCD (effetto fotoelettrico)
I CCD convertono i fotoni in cariche elettriche all’interno
di uno strato di silicio.
Queste cariche vengono misurate, digitalizzate e salvate
in un file immagine su un computer.
Maggiore sensibilità
Linearità
Immagini digitali