Uno sguardo su Pitagora
“Tutto è numero”
Sintesi di Tiziana Superchi
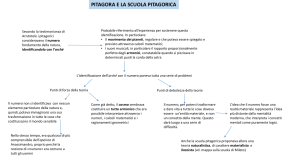
Alcuni aspetti fondamentali
Il grande contributo al pensiero
matematico :
Il misticismo bizzarro
del numero
Teoria degli
opposti
Introduce la
dimostrazione
come fondamento del metodo
deduttivo
Speculazioni
cosmiche
Teoria
dell’Aritmogeometria
Scoprì,
tra
umiliazione
e
sofferenza,
l’insufficienza
del
numeri interi ordinari, consentendo
la successiva applicazione dei
numeri irrazionali.
Pitagora fondatore intorno al 530 a.C. dell’omonima scuola a Crotone
nella Magna Grecia, è stato un mistico, un filosofo, un matematico e un
naturalista al tempo stesso.
Le sue speculazioni cosmiche si basavano su alcuni concetti.
Per Pitagora tutti fenomeni
naturali erano regolati da una
legge
matematica
da
lui chiamata Armonia. Solo chi
era in grado di capire le leggi di
questo equilibrio armonioso
poteva arrivare all’Assoluto.
La sua visione del cosmo era per quei
tempi rivoluzionaria, in quanto spiegava
agli allievi che al centro dell’universo
esisteva il Fuoco Centrale e intorno a
questo Fuoco ruotavano in orbite circolari
perfette la terra, la luna ed il sole, più i
pianeti allora conosciuti, emettendo una
musica armoniosa.
Nel Seicento quando, Copernico dichiarava che il suo sistema,
con la Terra che girava attorno al sole, era un sistema
“pitagorico” e lo stesso Galileo veniva considerato “pitagorico”,
poiché Pitagora veniva visto come il padre delle scienze esatte.
I Pitagorici applicarono i numeri alla loro
dottrina suddivisa in:
Aritmetica
Musica
Geometria
Astronomia
Anche la Teoria degli opposti,
come idea di una realtà fondata
sull’interazione tra gli opposti,
trova spiegazione nel concetto
di numero
Dieci sono le opposizioni
fondamentali.
Ambivalenza dell’unità: l’uno
non è né pari né dispari.
Opposizioni applicate ai numeri,
che assumono un valore
simbolico, magico e religioso
Furono evidenziate le 10 opposizioni fondamentali:
1) LIMITE - INFINITO
2) DISPARI - PARI
3) UNITA' - MOLTEPLICITA'
4) DESTRA - SINISTRA
5) MASCHIO - FEMMINA
6) QUIETE - MOVIMENTO
7) RETTA - CURVA
8) LUCE - TENEBRA
9) BENE - MALE
10) QUADRATO - RETTANGOLO
I Numeri principio di tutto
Pitagora, come profeta ispirato, predicava che tutta la natura,
l’universo intero, ogni cosa matematica, fisica, metafisica,
morale riposa sul modulo “discreto” del numero intero 1, 2, 3….e
può essere interpretato per mezzo di questi elementi datici da
Dio.
I numeri venivano rappresentati con ”unità-punto”, “atomimatematici” detti anche “monadi””disposti in modo che ad ogni
numero corrispondesse una figura geometrica:.
1
3
6
10
15
Numeri triangolari
1
4
9
Numeri quadrati
16
I pitagorici svilupparono un vero e proprio
culto del numero: immaginavano che ciascun
numero possedesse attributi particolari.
I Numeri erano divisi in pari e dispari, positivi e
negativi, maschili e femminili.
L'ordine e la perfezione stanno dalla parte dei
numeri dispari, mentre, al contrario, il disordine ed
il male stanno sempre dalla parte del pari.
Il numero 1 è il generatore dei numeri e il numero della ragione
Il numero 2 è il primo numero pari o femminile
Il numero 3 è il primo vero numero maschile, il numero
dell’armonia
Il numero 4 è il numero della giustizia o del castigo
Il numero 5 è il numero del matrimonio
Il numero 6 è il numero della creazione
Il numero 10 è il più sacro di tutti (sacra decade), il numero
dell’universo: tetractys=1+2+3+4
Teoria dell’Aritmogeometria
Collegamento fra numeri e figure geometriche;
Costruzione dei numeri mediante elementi discreti, sassolini;
Da tali costruzioni si potevano ricavare delle proprietà aritmetiche
e geometriche.
Ad esempio…..
1. Un generico numero triangolare Tn si ottiene sommando i primi n numeri
naturali:
T3=1+2+3=6
T4=1+2+3+4=10
2. Un generico numero quadrato Qn si ottiene sommando i primi n numeri
dispari, a partire dall’unità:
Q2=22=1+3=4
Q3=32=1+3+5=9
Q4 =42=1+3+5+7=16
Il contributo al pensiero matematico
In geometria Pitagora segnò il passaggio dalla matematica applicata,
fatta di regole empiriche, alla matematica astratta, grazie
all’introduzione di dimostrazioni fondate sul metodo deduttivo a
partire da assiomi esplicitamente formulati.
Ai pitagorici vengono attribuiti, fra le altre scoperte:
Il teorema sulla somma degli angoli del triangolo.
Il cosiddetto “teorema di Pitagora”
La risoluzione di parecchi problemi sulle aree, allora ancora insoluti.
La costruzione dei poliedri regolari.
I pitagorici studiarono, con particolare interesse , i
poligoni e i solidi regolari; il pentagono e la stella
pentagonale a cinque punte pare che avessero
affascinato talmente tanto il grande maestro che li
pose a simbolo della scuola.
Pitagora costruì le “figure cosmiche”, i cinque poliedri
regolari.
Secondo la filosofia del
tempo la natura era
costituita da particelle
piccolissime:
Tetraedri per il fuoco.
Cubi per la terra.
Ottaedri per l’aria.
Icosaedri per l’acqua.
Il dodecaedro era il
modello per l’universo.
La scoperta delle grandezze incommensurabili
Gli “oggetti” dei pitagorici avevano dunque una
consistenza “discreta” da cui derivava che tutte le
grandezze omogenee dovessero essere tra loro
commensurabili (cioè ammettere un sottomultiplo
comune, la monade) e che il loro rapporto dovesse
sempre essere espresso come rapporto tra due
numeri interi (cioè come numero razionale, la
frazione)
Un esempio: due segmenti
commensurabili
La scoperta delle grandezze incommensurabili
E fu proprio, ironia della sorte, un’applicazione del noto
teorema di geometria, che da Pitagora prese il nome, a
smentire le certezze che il matematico aveva fino ad allora
posseduto. Tale scoperta da cui Pitagora fu umiliato e
sconvolto, era dovuta all’impossibilità di esprimere il
rapporto tra il lato di un quadrato e la sua diagonale
attraverso il rapporto tra due numeri interi.
Sotto altra forma diremo che il numero
irrazionale.
2 è un numero
Naufragò in tal modo la teoria del “discreto” fulcro e fondamento di
tutta la filosofia pitagorica, per cedere il posto a quella del
“continuo”.
Gli oggetti astratti della geometria cominciarono ad essere
considerati come figure costituite da infiniti punti privi di
dimensioni, divisibili in parti piccole quanto si voglia e tali da
richiedere, per la loro misura, l’introduzione di un insieme
numerico più ampio, l’insieme dei numeri reali.