I_settembre_2004

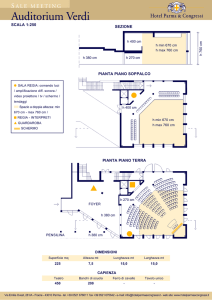
Prova di esame del corso di Fisica 4
I appello di Settembre del 13/9/04
NOME………….....….
A.A. 2003/4
COGNOME……………........………............
1) Un satellite geostazionario del sistema GPS irraggia nello spazio una potenza P = 100 W sotto forma di
onde radio monocromatiche. Assumendo che siano generate onde sferiche e che la propagazione sia nel vuoto,
si calcoli l’ampiezza del campo elettrico e del campo magnetico: (a) in prossimità della superficie del mare
sulla verticale del satellite, ovvero a circa 36000 km dal satellite; (b) appena sotto la superficie del mare
assumendo per l’acqua n = 2 alla frequenza del campo elettromagnetico
2) Nella figura un raggio di luce penetra in una lastra di vetro (posta in aria) nel punto A e subisce una
riflessione totale nel punto B. Cosa si può dedurre riguardo al valore dell’indice di rifrazione n del vetro?
45°
A
n
B
3) Una diapositiva di formato 24 mm  36 mm deve essere proiettata su uno schermo di 1.20 m per
1.80 m posto ad una distanza di 5.00 m dal proiettore. Determinare: (a) che tipo di lente (singola)
occorre usare e con quale lunghezza focale per coprire esattamente lo schermo con l’immagine; ( b)
quale sarà la distanza lente-diapositiva; se il proiettore produce un il flusso luminoso di 1000 lumen,
(c) che illuminamento (o illuminanza) si avrà sullo schermo?
A) Scrivere l’espressione del campo elettrico per un’onda elettromagnetica piana monocromatica di
lunghezza d’onda nel vuoto 0, con un’ampiezza del campo elettrico E0, polarizzata circolarmente che
si propaga lungo y in un mezzo con indice di rifrazione n.
B) Definire l’angolo di Brewster?
C) Cosa provoca e da cosa è causata l’aberrazione cromatica?
D) Si ricavi, mediante il tracciamento dei raggi, l’immagine corrispondente alla freccia oggetto
rappresentata e s e ne descriva le caratteristiche.
specchio
concavo
C
E) Perché i fari antinebbia sono gialli?
Soluzioni
I 
1)
P
4r 2
E0 
B0 
2 IZ0
E0
E
 0
v
c
sulla superficie del mare r =3.6  107 m e quindi:
I  6.14 10-15 W/m 2  E0  2.15 10- 6 V/m, B0  7.17 10-15 T
appena sotto la superficie del mare:
 n n  
 1 
   I 1      5.46 10 W/m
I '  I 1  
  n  n  
  3 
2
1
2
1
2
2
15
2
E '  2.03 10- 6 V/m, B'  1.35 10-14 T
2) dalla legge di Snell in A:
n
2
2 sin θ r
dalla condizione di angolo limite in B:
quindi:
3)
m
1-
1
2n 2

1
 n
n
s'
y ' 1200


 50
s
y
24
3
2
n
1
1

sin 90  θr 
cos θr
 n  1.22
 distanza  s 
s  s'
 9.8 cm
s' s
1
1
1


s
s'
f

illuminanz a 
1000 lumen
 463 lux
1.2 1.8 m 2
f 
5m
 10 cm
50