Q 2

Ciclo termico
“Ciclo termico”: trasformazione ciclica nella quale il sistema termodinamico
che compie il ciclo fornisce lavoro assorbendo complessivamente calore da
sorgenti di calore (“serbatoi”) esterni al sistema
Wciclo  Qciclo  Qass  Qced  Qass  Qced  0
U ciclo  0
Qass  Qced
essendo cioè:
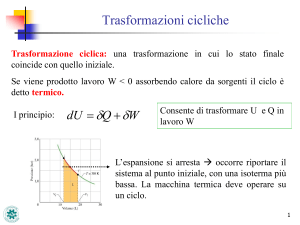
Se il sistema è un fluido le cui trasformazioni sono descritte nel piano (p,V) , il
lavoro è rappresentato dall’ area compresa nella curva chiusa rappresentativa
del ciclo: p
Wciclo=Qciclo > 0
V
Si definisce il “rendimento” di un ciclo termico la quantità:

U.Gasparini, Fisica I
Qced
Wciclo
Qass  Qced

 1
Qass
Qass
Qass
1
1
Ciclo di Carnot:
Ciclo reversibile compiuto da un gas ideale, costituito dalle seguenti trasformazioni :
A B : espansione isoterma reversibile alla temperatura T2
U = 0
Q 2 = WAB > 0
“serbatoio di
calore”
B C : espansione adiabatica reversibile
U = n cV(T1-T2) = -WBC < 0
Q=0
T2
C D : compressione isoterma reversibile alla temperatura T1 < T2
U = 0
Q 1 = WCD < 0
D A : compressione adiabatica reversibile
U = n cV(T2-T1) = -WDA > 0
Q=0
p
T1
A
Q 2 (calore assorbito alla temperatura
superiore)
B
T=T2
C
D
U.Gasparini, Fisica I
VA
T=T1
Q 1 (calore ceduto alla temperatura inferiore)
VD
VB
VC
V
2
Calori scambiati nel ciclo di Carnot :
p
A
Q2
B
T=T2
D
Q1
VA
VD
VB
T=T1
C
VC
V
VB
Qass  Q2  WAB 

VB
VA
VD
Qced  Q1  WCD 

p(V ) dV  nRT2

VA
VD
VC
Qced
Qass

p(V ) dV  nRT1
VC


T2 lnV B
 VB 
dV

 nRT2 ln
V
 VA 
 VD 
dV

 nRT1 ln
V
 VC 

/ VA 
T1 ln V D / VC
Dall’equazione della adiabatica reversibile di un gas ideale:

TBVB
1
 1
TAV A
 VB 


 VA 

 TCVC
1
 1
 TDVD
 1
V 
 C
 VD 
 1


TBVB
1
 1
TAV A


TCVC
1
 1
TDVD
V 
V 
ln B    ln D 
 VA 
 VC 
Qced
T
  1
Qass
T2
Rendimento del ciclo di Carnot
Il rendimento di un ciclo termico è :



Per il ciclo di Carnot:
Qass  Qced
Qced
W

 1
Qass
Qass
Qass
  1
T1
T2
Il rendimento di un ciclo di Carnot dipende unicamente dalle temperature T1 e
T2 tra le quali avviene il ciclo:
non dipende dal tipo di gas impiegato, nè dall’intervallo di pressioni e volumi
considerato:
T=T2
p
  '
Q2
Q’ 2
T=T1
W’
W
U.Gasparini, Fisica I
Q1
Q’ 1
V
4
Ciclo di Stirling:
Ciclo reversibile di un gas ideale costituito da due isoterme e due isocore
gli scambi termici avvengono con un numero infinito di sorgenti
p
A
Q AB
Q DA
B
T=T2
Q BC
D
Si ha:
VA=VD
T=T1
C
Q CD
V
VB=VC
QDA  U DA  ncV (TA  TD )  ncV (TC  TB )   U BC  QBC
WDA  0

WBC  0
Qciclo
Q AB  QCD
WCarnot
WCarnot
W




 Carnot
Qass
Qass
Q AB  QDA
Q AB  QDA
Q AB
( si osservi che:
A
WCarnot  QAB  QC ' D'  QAB  QCD
B
essendo:
QC ' D'  nRT1 ln(VD' / VC ' )  nRT1 ln(V A / VB )
U.Gasparini, Fisica I  nRT ln(V / V )  Q
1
D
C
CD
)
D
D’
C
C’
5
“ Ciclo frigorifero” :
Il sistema termodinamico compie una trasformazione ciclica assorbendo
complessivamente lavoro e cedendo calore :
Qciclo  Wciclo  0
p
Qciclo=Wciclo< 0
V
Esempio: ciclo frigorifero di Carnot :
p
Q 2 < 0 (ceduto)
T=T2
T=T1
W<0
U.Gasparini, Fisica I
Q2  Q1
Q 1 > 0 (assorbito)
V
Qciclo  Q1  Q2  0
6
“Efficienza” o “coefficiente di prestazione”
“Efficienza” in un ciclo frigorifero:
Qass

Wciclo
(N.B.: a differenza del rendimento, può essere : > 1 )
Per un ciclo frigorifero di Carnot :
 

Qass
Wciclo

Q1
Q1  Q2

Q1
1


 ( Q1  Q2 )
 1  Q2 / Q1
1
1

nRT2 ln(V A / VB )
 1  T2 / T1
 1
nRT1 ln(VC / VD )
p
A
Wciclo < 0
T1
T2  T1
Q 2 =nRT2 ln(VA / VB ) < 0 (ceduto)
B
D

 
T=T2
C
T=T1
Q 1 =nRT1 ln(VC /VD ) > 0 (assorbito)
l’efficienza del ciclo frigorifero tende a zero quando tende a zero V
la temperatura assoluta della sorgente alla quale si sottrae calore
7
Fluidi reali
Il comportamento di un fluido reale è descritto nel piano (p,V) dal
“diagramma di Andrews”:
p
gas
“isoterma critica” T TC
S-L
Pressione di
punto triplo
L
G
liquido-vapore
S
ptr
solido-vapore
p
S
ptr
L
Ttr
“punto
triplo”
“curva di sublimazione”
isoterma
T =Ttr
“curva di
evaporazione”
V
vapore
V
Equilibrio
solido-liquido-vapore : p = ptr ,
Descrizione “tridimensionale”
nello spazio (p,V,T):
“curva di
fusione”
“curva di Andrews”
T
T=TC
T=T2
T=T1
T=Ttr
V
Diagramma p-T :
(
curva di fusione
dp( T )
 0
dT
p
“pressione di fusione”
(es.:H2O)
dp( T )
0
dT
)
gas
liquido
curva di evaporazione
solido
ptr
vapore
punto triplo
curva di sublimazione
Ttr
TC
T
L’andamento p(T) della pressione di evaporazione (pressione alla quale si ha la
transizione liquido-vapore ad una data temperatura, “tensione di vapore saturo”) è
data dalla eq.di Clapeyron:
dp


dT
T (vV  v L )
volume specifico
nella fase di vapore
calore latente di evaporazione
vol. spec.nella
fase liquida
che è ricavabile sulla base di considerazioni termodinamiche molto generali.
U.Gasparini, Fisica I
9
Equazione di Clapeyron
Consideriamo infatti un ciclo di Carnot “infinitesimo” (ossia tra due isoterme a distanza
infinitesima dT) utilizzando come sostanza un vapore saturo:
p
curva di Andrews
T+dT
T
VL
volume del ” liquido saturo”
V
VV
volume del ” vapore saturo”
Il rendimento del ciclo di Carnot non dipende dalla sostanza che compie il ciclo, e vale:
  1
D’altra parte:

T
1
dT 
dT

 1
 1  1 
 

T  dT
1  dT / T
T 
T
dp(VV  V L )
W

Qass
m
dove si sono introdotti i volumi specifici:
e quindi:
U.Gasparini, Fisica I
dp


dT
T (vV  v L )
dp( vV  v L )
dT

T

vV , L 
VV , L
m
10
Trasformazioni di fase
L’eq. di Clapeyron è inoltre valida per una generica trasf.di fase 1 2 :
dp


dT
T (v2  v1 )
calore latente della trasf.
Per trasf. L  V e S  V è sempre:
vV  v L
vV  v S
e
( ossia, per le densità: V   L , S
)
dp
 0
dT

(le curve p(T) di evaporazione e di sublimazione nal piano (p,T) hanno sempre
pendenza positiva ; cfr. slide nr. 9)
Per trasf. S  L si possono avere diversi comportamenti:
- per la maggioranza delle sostanze :
v L  vS
 L  S

dp
0
dT
vi sono però importanti eccezioni, come l’acqua :
v L  vS
 L  S
U.Gasparini, Fisica I
(il ghiaccio galleggia)

dp
0
dT
11
Trasformazione di fase liquido-vapore
Per la trasformazione di fase liquido-vapore, l’eq. di Clapeyron , con alcune
approssimazioni generalmente ben verificate, può essere facilmente integrata:
dp


m
mp




dT
T (vV  v L )
TvV
TV
nRT 2
dp
AdT

p
RT 2
ln p 
vV  v L
con :
 A
C
RT
vapore gas ideale: V= nRT /p
A  m/ n
massa molare
assumendo  indipendente dalla
temperatura (ciò è vero se si è abbastanza lontani
dal “punto critico”)
La “tensione di vapor saturo” ad una data temperatura T aumenta con la
temperatura:
p(T )  p0e  A/ RT
p
solido
ptr
U.Gasparini, Fisica I
liquido
vapore
gas
12
punto triplo
T