Figura 2: in una trasformazione isocora ( a - Digilander

ENERGIA , LAVORO E CALORE IN UN GAS
Adesso finalmente possiamo affrontare il cuore della Termodinamica:
studiare le leggi che governano la trasmissione di energia da parte
di un gas. Per capire qual è l’importanza di questo argomento e come
mai esso venga affrontato in un corso di Agraria, tenete conto che,
qualunque macchina operatrice vogliate usare, tutta l’energia che
sfruttate la ottenete
–eccetto limitatissime eccezioni- da una
trasformazione termodinamica di un gas. Pensate ad una pompa
irrigatrice: essa spinge fuori l’acqua applicando una pressione al
fluido. Questa pressione trasferisce energia al fluido, come abbiamo
già descritto negli appunti “DINAMICA DEI LIQUIDI – cenni-“. Da
dove arriva questa energia? Chiaramente, essa proviene dal motore a cui è agganciata la pompa. E come
funziona questo motore? Bruciando gasolio o benzina nei cilindri del motore, dove un pistone viene
continuamente spinto e richiamato dalla ciclica espansione/compressione di un gas riscaldato. E questo vale
per praticamente ogni strumento che utilizzerete… Perciò è bene avere almeno un’idea generale di come un
gas assorba/riceva energia se volete avere almeno una visione essenziale di come viene generata tutta
l’energia che utilizzerete.
“Che barba! Un altro pacco di formule da memorizzare!” Ed invece no, e questo è il bello: in realtà noi già
conosciamo tutte le equazioni essenziali associate all’energia di un gas! Infatti:
il Lavoro di un gas (L) è quello prodotto dalla pressione del gas che si espande: perciò esso obbedisce alle
leggi che già abbiamo imparato riguardo al Lavoro prodotto da una pressione:1
L=pV
(1) , con p la pressione del gas e V la sua variazione di volume.
se il gas si espande: V>0 , L>0 ed il gas esegue Lavoro sull’ambiente
esterno, trasferendogli energia
se il gas si contrae: V<0 , L<0 ed il gas riceve Lavoro dall’ambiente
esterno, ricevendo da esso energia
il calore scambiato da un gas (Q) segue le stesse identiche leggi del calore che sappiamo valere per ogni
sostanza:2
Q = cmT
(2) , con c il calore specifico del gas , m la sua massa e T la sua variazione di
temperatura.
L’unica –importante!- differenza fra il riscaldamento di un gas e quella di un solido/liquido è che il primo può
essere compresso espando (un gas non ha volume proprio), cosicché un gas non ha un unico calore specifico
ma piuttosto un calore specifico per ogni tipo di trasformazione che subisce.
In particolare, se il gas è riscaldato a volume costante (il gas è rinchiuso in un ambiente sigillato) il suo
calore specifico si indica con cv (calore specifico per un’isocora); se è riscaldato a pressione costante (il
gas è tenuto all’aria aperta) il suo calore specifico si indica con cv (calore specifico per un’isobara).
Q = cpm T
(3a)
per calcolare il calore assorbito/ceduto in una trasformazione isobara
Q = cvmT
(3b)
per calcolare il calore assorbito/ceduto in una trasformazione isocora
Come voi sapete, in Chimica e più in generale quando si parla di gas non si esprime la sua massa in grammi o
chili ma si usa il suo numero di moli (n): in questo caso al posto della massa m va usato n:
1
2
Negli appunti “DINAMICA DEI LIQUIDI – cenni”
Negli appunti”COME SI RISCALDANO I MATERIALI:…”
Q = cpn T
(3a)
per calcolare il calore assorbito/ceduto in una trasformazione isobara
Q = cvnT
(3b)
per calcolare il calore assorbito/ceduto in una trasformazione isocora
Analogamente, si definisce la capacità termica C a secondo della trasformazione seguita dal gas:
Q = Cp T
(4a)
per calcolare il calore assorbito/ceduto in una trasformazione isobara
Q = CvT
(4b)
per calcolare il calore assorbito/ceduto in una trasformazione isocora
I calori specifici cambiano da gas a gas: fissato il tipo di gas, essi rimangono praticamente costanti al cambiare
della pressione e della temperatura, purché il gas possa essere considerato perfetto. Nella Tabella sotto sono
indicati quelli dei gas più importanti.
Nota che cp > cv, sempre. Questa proprietà, apparentemente marginale, è invece alla base della produzione
di Lavoro da parte di un gas: la spiegheremo fra poche pagine.
IL CALORE E’ UNA FORMA DI ENERGIA
Notate una cosa: i calori specifici della Tabella non sono espressi in calorie ma in Joule! O questa? L’unità di
misura del calore è la caloria… mentre il Joule è l’unità di misura del Lavoro e dell’energia in generale.
E’ stata una fondamentale scoperta di metà 1.800 che il calore altro non è che una forma di energia e
che perciò può essere misurato indistintamente sia in calorie sia in Joule (non ci credete? Guardate i valori
calorici stampati sulle etichette dei cibi che comprate: essi sono generalmente espressi sia in Kcal che in KJ).
E’ stato misurato che 1cal corrisponde a 4,186J: cioè, tutte le volte che 4,186J di Lavoro vengono trasformate
in calore, ad esempio per attrito, esse producono 1caloria; viceversa, se l’espansione di un gas assorbe
1caloria ciò significa che il gas può produrre 4,186J di Lavoro. Questo discorso è approfondito negli appunti
“CALORE E LAVORO-relazione sperimentale”: per quanto riguarda i problemi che affronteremo è sufficiente
sapere che calore e Lavoro sono trasformabili uno con l’altro con l’equivalenza:
Q = 4,186L
, Q in calorie, L in Joule
PROBLEMI INTRODUTTIVI
Troppi simboli a giro? Riorganizziamo il tutto facendo alcuni semplici esempi.
Riguardo alla pressione, per comodità considereremo l’approssimazione3 :
100.000 Pa = 1 bar = 1atm = 10m d’acqua = 760mmHg
Sempre per semplicità, consideriamo di arrotondare il passaggio da Celsius a Kelvin (e viceversa) con la
formula:
TKELVIN = TCELSIUS + 273 (invece che +273,15)
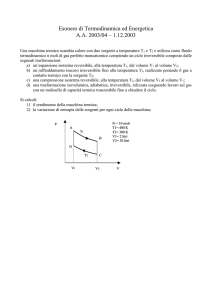
Problema1: Lavoro e calore. Adesso risolviamo un semplice problema che illustra qual è il significato pratico
di tutti i discorsi fatti finora. Calcoleremo il calore necessario a far espandere un gas ed il Lavoro prodotto da
questa espansione. Considera di avere 10 moli di aria (l’aria alla temperatura e pressione ambiente è
praticamente un gas perfetto) contenuta dentro un cilindro. Considera che la temperatura iniziale del cilindro
sia T1=20°C e la sua pressione iniziale P1=1atm: con un rapido calcolo (quale? Fallo tu usando l’equazione di
stato dei gas perfetti!) risulta che il volume iniziale è V1=243,6 litri.
Adesso riscaldi il gas: esso si dilata isobaricamente (il pistone è a diretto contatto con l’atmosfera, perciò
p=1atm durante tutta la trasformazione), fino a giungere alla temperatura di 200°C. Ti chiedo:
1) Quanto calore hai dovuto fornire? [Q=52.380J]
2) Quanto Lavoro ha eseguito il pistone sollevandosi? [L=14965J]
Figura 1: fornendo calore Q al gas dentro il cilindro: il gas si espande ed è in
grado di sollevare il pesetto posto sopra di esso, eseguendo così un Lavoro
3
Come discusso negli appunti “PROBLEMI CON STEVINO”
Soluz:
1) la trasformazione è isobara: Q = cpARIAnT ;
il calore specifico dell’aria è praticamente quello
dell’azoto  cpARIA=29,1J/mol
T=200°C-20°C = 180°C (non ha importanza esprimere la temperatura in Kelvin o in Celsius perché si
ottiene sempre la stessa variazione di temperatura, come detto a lezione. Se non ci credi, porta tutto in
Kelvin e calcola nuovamente T!)
Q = cpARIAnT  Q = 29,110180 = 52.380 J di calore
L=pV ; p = 1atm = 100.000Pa. Devo calcolare V. La trasformazione è isobara: uso la 1° legge di
Gay-Lussac, valida per le isobare: V1/T1=V2/T2 , T espresso necessariamente in Kelvin.
V2 = V1(200+273)/(20+273) = 393,25L
Adesso sono in grado di calcolare di quanto si è espanso il gas:
V= V2-V1 = 393,25L - 243,6L = 149,65L = 0,14965m3. Il gas si è espanso di 0,14965m3.
L=pV  L = 100.0000,14965m3 =14.965J
Problema2: Differenza fra cp e cv. Adesso vedremo con un semplice esempio perché al cambiare del tipo di
trasformazione cambia anche il calore specifico. Stai bene attento, perché questa differenza, che può
sembrare poco più di una curiosità, è alla base dello scambio di energia da parte di un gas.
Considera di avere le stesse 10 moli di aria alle stesse identiche condizioni iniziali del Problema1. Considera di
riscaldare il gas fino a 200°C ma stavolta tenendolo sigillato a volume costante (trasformazione isocora).
Calcola il calore necessario ed il Lavoro eseguito [ Q=37.440J , L=0J ].
Soluz: Poiché la trasformazione è isocora, uso cv invece che cp.
Q = cvnT  Q = 20,810180 = 37.440 J
L = pV  L = 0J . Infatti, in un’isocora V=0, il gas non si espande né si comprime e dunque
non esegue alcun Lavoro.
“Che bello! Ho calcolato il calore scambiato da una isocora. Ora però sul perché ogni trasformazione ha
bisogno di un suo calore specifico ne so quanto prima.”
Studente, prima di protestare sta’ attento: confronta i valori del Problema1 con quelli del Problema2.
Nell’isobara: Q=52.380J , L=14965J
Nell’isocora: Q=37.440J , L=0J
Se fai i conti, vedrai che il calore necessario per la trasformazione isobara è praticamente uguale (entro gli
errori di approssimazione dei valori usati) alla somma del calore isocoro (cioè quello usato solo per riscaldare)
+ Lavoro! In pratica, nell’isobara hai dovuto fornire calore sia per riscaldare il gas (lo hai portato da 20°C a
200°C) sia per fargli fare Lavoro; in un’isocora hai dovuto fornire calore solo per scaldarlo: questo spiega
perché hai dovuto usare meno calore e perciò perché cv < cp. Questo spiega anche perché ogni
trasformazione ha il suo calore specifico: bisogna considerare non solo il calore necessario a scaldare il gas ma
anche quello che deve essere assorbito/ceduto a causa del Lavoro eseguito durante l’eventuale
espansione/compressione (ed ogni trasformazione espande/contrae il gas in modo diverso).
Il fatto che la trasformazione isobara abbia avuto necessità di un calore maggiore per poter produrre Lavoro
dimostra che è possibile trasferire calore in Lavoro e perciò è possibile produrre macchine che sfruttino il
calore per produrre Lavoro. Questo tipo di macchine si chiamano macchine termiche e sono alla base di
praticamente tutta l’energia che otteniamo.
Figura 2: in una trasformazione isocora ( a sinistra) il volume del gas non cambia e perciò il calore va
esclusivamente ad innalzare la temperatura; in una trasformazione isobara o comunque non-isocora il gas
solleva il pistone di un tratto h, espandendosi si un volume V, producendo in questo modo un Lavoro
pV0: in questo secondo caso hai bisogno di calore sia per scaldare il gas sia per produrre il Lavoro
dell’espansione.
MACCHINA TERMICA - intro
Adesso siamo in grado di capire il funzionamento essenziale di una macchina termica, cioè di una macchina
in grado di convertire calore in Lavoro, come il nostro piccolo pistone del Problema1. E’ chiaro che una tale
macchina, per fornire Lavoro, deve far espandere del gas: il gas per espandersi deve venire riscaldato e perciò
a tale macchina dobbiamo fornire calore dall’esterno –ad esempio, bruciando gasolio-. Una volta che il gas si è
espanso… ha finito di eseguire il suo Lavoro! Deve perciò venir compresso di nuovo al valore di partenza,
raffreddandolo e disperdendo il calore in eccesso. A questo punto la macchina è pronta per un secondo ciclo di
riscaldamentoespansioneLavororaffreddamento
Una macchina che produce Lavoro eseguendo questo ciclo si chiama macchina termica ciclica. In pratica,
quasi tutte le macchine termiche sono cicliche.
La macchina termica più semplice che sfrutta il ciclo di cui sopra è probabilmente la macchina a vapore, che è
schematizzata negli appunti “MACCHINE TERMICHE”.
BILANCIO ENERGETICO DI UNA MACCHINA TERMICA ED EFFICIENZA
Adesso fate un ultimo sforzo e studiate queste semplici formule che vi propongo: esse sono alla base della
comprensione di tutta la produzione di Lavoro da parte di una qualsiasi macchina termica ciclica.
All’inizio bisogna avere un cilindro con un pistone mobile, come quello di Figura 1: il cilindro deve essere pieno
di gas da far espandere, non importa quale sia il gas tanto praticamente tutti gas in condizioni ambiente sono
perfetti e perciò le loro proprietà non dipendono dalla loro composizione.
A questo punto si scalda il cilindro! Non importa come sia scaldato, l’importante è che gli sia fornito calore. Il
calore (Qass) fornito viene assorbito dal gas che si riscalda e si espande: il tipo di espansione dipende dalla
velocità con cui avviene l’espansione. Se l’espansione è lenta il gas si espande isotermicamente, se invece è
molto veloce avviene adiabaticamente4. Se non hai ben chiaro cosa siano queste due trasformazioni non
importa, l’importante è che sia chiaro che il gas produce Lavoro (L) quando si espande.
Nota che quando riscaldi il gas avvengono due fenomeni ben distinti: il gas si riscalda + il gas si espande. Ne
segue che parte del calore Qass va a scaldare il gas e parte va a fornire l’energia per l’espansione. Se Qs è la
parte di calore che va a scaldare il gas e L è il Lavoro fatto dall’espansione, posso scrivere:
Qass = Qs + L
(1) (esprimo il calore in Joule, secondo l’equivalenza 1caloria =
4,186J )
Posso descrivere l’eq. (1) con una semplice frase: “Se ad un gas fornisco un’energia Qass, una parte di questa
va a scaldare il gas (Qs) mentre la restante parte è sfruttata per espandersi ed eseguire lavoro (L)”.
4
Per conoscere le proprietà di queste trasformazioni, leggi gli appunti “TRASFORMAZIONI
TERMODINAMICHE”
A questo punto ho il mio bel pistone che si è espanso… e ora cosa facciamo? Bisogna riportarlo indietro in
modo che chiuda il ciclo! E’ necessario raffreddarlo, cosicché esso si ricontragga e torni al punto di partenza.
Chiamiamo Qced il calore che è necessario estrarre dal gas per raffreddarlo: poiché esso è tornato
esattamente al punto di partenza, questo calore deve essere esattamente uguale a quello sfruttato per
scaldarlo, cioè:
Qs = Qced
(2)
(Qced in valore assoluto)
Adesso sono in grado di calcolare il Lavoro prodotto dalla macchina termica: usando l’eq. (2) posso
scrivere l’eq. (1) come:
L = Qass – Qced
(3)
(anche qui Qced in valore assoluto)
Dunque: il Lavoro utile di un motore è esattamente uguale al calore assorbito (Qass) meno quello
disperso (Qced , quest’ultimo in valore assoluto)
Per avere un esempio di come praticamente funzioni una macchina termica, leggiti gli appunti “MOTORE A
SCOPPIO” che descrivono il funzionamento –non a caso- di un motore a scoppio; in tali appunti vi sono anche
dei link (che puoi trovare comodamente sul mio sito) che ti fanno vedere come tutto ciò che abbiamo detto
finora viene messo in pratica.
PROBLEMI INTRODUTTIVI
Adesso risolveremo qualche semplice problema per applicare praticamente ciò che abbiamo detto finora.
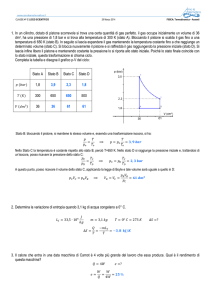
Problema1:
il ciclo di Otto. Immagina una macchina
termica che funziona in questo modo: hai un
cilindro+pistone come quello di Figura1, contenente 0,26
moli di aria: riscaldi il cilindro improvvisamente, cosicché il
gas non faccia in tempo ad espandersi durante il
riscaldamento ed il calore venga assorbito a volume
costante (riscaldamento isocoro). A questo punto il gas già
caldo si espande rapidamente (espansione adiabatica,
senza perdere calore) e solleva il pistone facendo Lavoro.
Arrivato al massimo dell’espansione, fai uscire l’aria calda
rapidamente, raffreddando il tutto (raffreddamento
isocoro); il pistone rapidamente si contrae tornando al
punto di partenza, pronto per un altro ciclo (compressione
adiabatica) -in pratica, è lo schema essenziale di un
motore a scoppio 4tempi, il cosiddetto ciclo di Otto-. Il
grafico V-p di tale ciclo è mostrato in Figura 3
La fase AB è quella in cui il cilindro fa entrare aria
La fase CD è quella di riscaldamento isocora;
La fase DE è quella di espansione adiabatica
La fase EB è quella di raffreddamento isocoro
La fase BC è quella di compressione adiabatica.
La fase BA è quella in cui il cilindro espelle l’aria
Hai misurato che:
le moli del gas sono 0,26 ;
VA = VC = VD = 1L ; VB=VE=8L ;
TB=370K ; TC=700K ; TD=2400K ; TE=1100K
Trova il Lavoro prodotto dal pistone [L=5245,8J]
Figura 3
Soluz: a questo punto, è facile che molti di voi trovino il compito richiesto del tutto impossibile:
non scoraggiatevi! Dopo un paio di semplici considerazioni, il problema si risolve quasi da solo.
La fase AB e quella BA non hanno alcuna influenza sull’energetica perché sono solo il
carico/scarico dell’aria.
Il Lavoro si trova grazie all’eq. (3): L = Qass – Qced . Bisogna perciò trovare il calore assorbito
(Qass) e quello ceduto (Qced).
calcolo di Qass: l’unica fase di riscaldamento è quella isocora CD , cosicché Qass = cvnT.
cv = 20,8J/mole ; n=0,26 ; T=(TD-TC)=(2400K–700K)=1700K  Qass=20,80,261700
= 9193,6J
calcolo di Qced: l’unica fase di riscaldamento è quella isocora EB , cosicché Qced = cvnT.
cv = 20,8 J/mole ; n=0,26 ; T=(TB-TE)=(370K–1100K)=-730K Qass=20,80,26(-730)
=-3947,8J Il segno “-“ in Qced significa che esso è calore disperso e perciò perduto via: nei
conti dobbiamo però usare solo il valore assoluto, come già spiegato.
calcolo del Lavoro: L = Qass – Qced  L = 9193,6 J – 3947,8J = 5245,8J
EFFICIENZA DEL MOTORE
Una proprietà molto importante del motore è quella di convertire la massima quantità possibile di calore
assorbito in Lavoro; maggiore è la proporzione di energia che finisce in Lavoro (e dunque minore è la
proporzione di energia spesa per raffreddare il motore) meno calore devo fornire al motore per eseguire un
determinato Lavoro (e meno devo spendere in carburante per portare avanti la mia attività).
Il rapporto fra Lavoro usato ed Energia spesa si chiama efficienza (), come già detto in altri appunti5 :
Efficienza==(Lavoro prodotto)/(Energia spesa) 
=L/Qass
Adesso calcoliamo l’efficienza del nostro pistone:
Problema2: un pistone abbastanza efficiente. Quante energia è stata utilizzata dal mio cilindro per eseguire il
Lavoro rispetto a quella che gli ho fornito? Quanta, in proporzione a quella fornita, se ne è andata via dispersa
nell’ambiente del tutto inutilizzata?
Soluz: L’energia consumata dal cilindro è Qass=9193,6J , quella utilizzata come Lavoro è
L=5245,8J , quella dispersa nell’ambiente è Qced=3947,8J.
=L/Qass   = 5245,8J/9193,6J = 0,57 = 57% ; Qced/Qass = 0,43 = 43%
Che senso hanno tutti questi numeri? Descriviamo a parole i calcoli eseguiti:
“il mio pistone, tutte le volte che gli fornisco un calore pari a 9193,6J si espande da 1 litro ad 8 litri eseguendo
un Lavoro pari a 5245,8J. Dopo che l’espansione è terminata io devo raffreddare il cilindro per farlo ripartire
daccapo e devo togliergli 3947,8J di calore, che sono così inutilizzabili per fare Lavoro perché finiscono come
calore disperso nell’ambiente fuori dal cilindro. Fatti tutti i conti, il mio pistone è riuscito a trasformare in
Lavoro il 57% dell’energia che gli ho fornito mentre ha disperso nell’ambiente come calore il restante 43%.”
Posso perciò riassumere l’ultima frase affermando: “il mio pistone ha un’efficienza del 57%”.
5
Negli appunti “MOTORE A SCOPPIO”
Problema3:
una macchina termica assorbe 300cal ad ogni ciclo e produce 320J di Lavoro. Qual è il calore
che viene disperso? Qual è l’efficienza?
Soluz: In pratica, per una macchina termica ho una sola equazione utile: L = Qass – Qced.
Per poter confrontare calore e Joule, trasformiamo la caloria in Joule (1caloria = 4,186 Joule):
Qass = 300cal = 1255,8J.
L = Qass – Qced  320J = 1255,8J – Qced  Qced=935,8J;
 = L/Qass  =320J/1255,8J = 0,255 = 25,5%
Problema4:
la scelta del motore! Fra il pistone del Problema1-2 e la macchina del Problema3 quale
sceglieresti se vuoi produrre Lavoro spendendo meno soldi possibile per il carburante?
Soluz: il cilindro+pistone del Problema1 trasforma in Lavoro utile il 57% del calore assorbito, la
macchina del Problema3 è capace di utilizzare solo il 25,5% del calore ricevuto, meno della metà
del cilindro+pistone. Dunque, acquisti il cilindro+pistone.
E con questo semplice problema dovreste aver capito qual è l’aspetto pratico di tutti questi conti…
Problema5:
i cicli del motore. Il tuo motore genera un Lavoro di 12J ad ogni ciclo e il motore esegue 2000
cicli ogni minuto (2000rpm). Se l’efficienza del motore è =35%, qual è il consumo di calorie del tuo motore in
1h di attività?
Soluz: il Lavoro eseguito in un’ora è il Lavoro eseguito in 1minuto moltiplicato 60.
L1MINUTO = (12J al ciclo)2000cicli = 24.000J
L1h = (24.000J al minuto)60minuti = 1.440.000 J
Se l’efficienza è 35% vuol dire che 1.440.000J sono solo il 35% della spesa calorica, cioè
=L/Qass  L=35%Qass  Qass = L/0,35 = 1.440.000J/0,35 = 4.114.286J =
982.868calorie = 982,868Kcal
Problema6:
il motore number 2. Dopo aver provato il motore del Problema1, si è deciso di sperimentare un
nuovo tipo di motore il quale è identico a quello del Problema1 ma che assorbe il doppio di calore
(Qass=9193,6Jx2=18.387,2J). Di conseguenza, cambia la temperatura TD (quella dopo il riscaldamento) e TE
(quella dopo l’espansione da D); misuri che adesso TE=1785K (il valore di TD non ha importanza per i calcoli da
fare in questo problema). Trova quanto Lavoro produci in una singola espansione e qual è l’efficienza.
Soluz: L = Qass – Qced ; Qass = 18.387,2J . Bisogna calcolare Qced.
Qced = cvnT
Qced=20,80,26(370K-1785) = -7652,3J (ricordati che per i calcoli devi usare Qced in valore
assoluto)
L = Qass – Qced  L=18.387,2J – 7652,3J = 10.734,9J
=L/Qass  =10.734,9/18.387,2 = 58,4%
Nota che l’efficienza è lievemente aumentata. Questa è una regola generale: più viene riscaldato il
gas nella fase di riscaldamento maggiore è l’efficienza finale anche se, come puoi vedere tu stesso,
l’incremento di efficienza ottenuto è minimo.