Diapositiva 1

Trasformazioni cicliche
Trasformazione ciclica: una trasformazione in cui lo stato finale
coincide con quello iniziale.
Se viene prodotto lavoro W < 0 assorbendo calore da sorgenti il ciclo è
detto termico.
I principio:
dU  Q  W
Consente di trasformare U e Q in
lavoro W
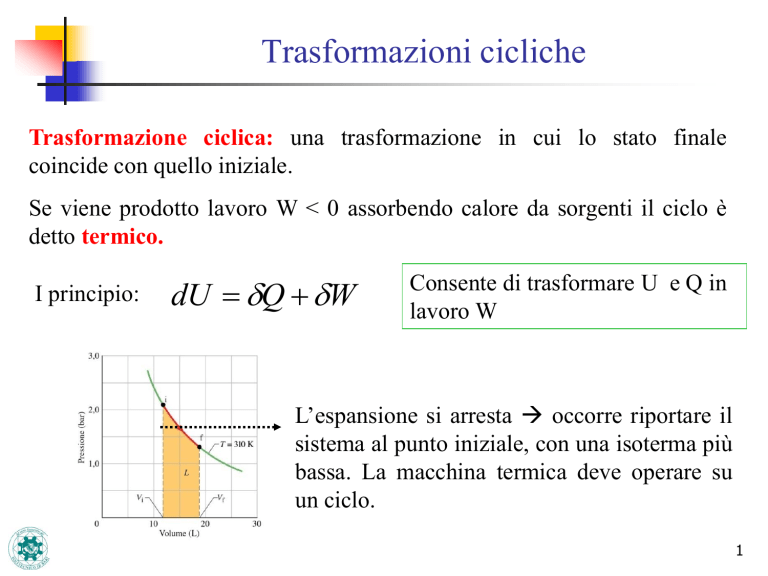
L’espansione si arresta  occorre riportare il
sistema al punto iniziale, con una isoterma più
bassa. La macchina termica deve operare su
un ciclo.
1
Ciclo di Carnot
 Motore termico è un dispositivo che scambia calore con l’ambiente e produce
lavoro. Affinché il lavoro venga prodotto in modo continuativo deve operare in
modo ciclico.
 macchina reversibile che opera tra due sorgenti
 2 isoterme + 2 adiabatiche
 può essere percorso da qualsiasi fluido motore:
prendiamo il gas perfetto.
2
Ciclo di Carnot
AB: espansione isoterma
U  0
b dV
nRT1
Wab    PdV   
dV  nRT1 

a
a
a V
V
Vb
b
 nRT1 ln V a  nRT1 ln
0
Va
b
Q1  WAB  0
b
Assorbito
3
Ciclo di Carnot
BC: espansione adiabatica
Ubc  nC V T2  T1 
Q0
Wbc  U bc nCV T2  T1   0
Cd: compressione isoterma
U  0
Vd
Wcd  nRT2 ln
0
Vc
Q2  WCD  0 Ceduto
4
Ciclo di Carnot
DA: compressione adiabatica
Uda  nC V T1  T2 
Q0
Wda  U da  nCV T1  T2   Wbc  0

Rendimento del ciclo:
Wtot
Qass

Qass  Qced
Qass
Vd
nRT2 ln
Vc
 1
Vb
 nRT1 ln
Va
 1
Qced
Qass
5
Ciclo di Carnot
ab isoterma
Pa Va  PbVb
bc adiabatica
PbVb  Pc Vc
cd isoterma
Pc Vc  PdVd
da adiabatica
PdVd  Pa Va
Moltiplicando tutti i primi membri e tutti i secondi membri tra loro




PaVaPb Vb PcVcPdVd  PbVb PcVc Pd Vd Pa Va
V
ln c
Vd
T
  1 2
T1 ln Vb
Va
 1
Vb 
 
Va 
1
Vc 
  
Vd 
T2
  1
T1
Vb Vc

Va Vd
6
Applicazione: il Ciclo Otto
Una macchina termica a combustione interna, il motore dell'automobile a benzina, può essere
approssimata con il ciclo mostrato in figura. Si supponga che la miscela aria-benzina possa essere
considerato un gas perfetto e che venga utilizzato un rapporto di compressione 4 a 1 (V4 = 4V1). Si
supponga inoltre che p2=3p1. Determinate la pressione e la temperatura in ognuno dei quattro vertici
del diagramma p-V in funzione di p1 e T1, e del rapporto g dei calori specifici del gas. Esprimere il
rendimento del ciclo in funzione del rapporto di compressione. Confrontare con il rendimento di una
macchina di Carnot che lavora tra le temperature estreme.
3p1
V2  V1
2
Adiabatica
Scoppio
3
p1
1
Adiabatica
4
V1
V4
P2  3P1
PV
3P1V1
T2  2 2 
 3T1
P1V1
nR
R
RT1
V3  V4  4V1
V2
V1

P3  P2   3P1    3  4 P1
V3
4 V1
P3V3 3  4  P1  4  V1
T3 

 3  41 T1
PV
nR
R 1 1
RT1
7
Applicazione: il Ciclo Otto
V4  4V1
V1
V1

P4  P1   P1    4 P1
V4
4 V1
P4V4 4  P1  4  V1
T4 

 41 T1
PV
nR
R 1 1
RT1

4
nC V T4  T3 
W
Qced

1 
1 
 1
Qass
Qass
nC V T2  T1 
1 
1 
3 4
3 1T1
T
1
41 1  3
1
1
 1   1
3  1
4
T4
41  T1
1
C  1
 1
1 
1
T2
3T1
34
8
Il frigorifero





Il ciclo di Carnot è un ciclo reversibile
Quindi può essere percorso al contrario:
 Si invertono i segni degli scambi energetici
 Cambia segno U - W e Q
 Quelle
che erano le quantità assorbite
diventano cedute e viceversa
quindi la macchina di Carnot al contrario
 assorbe il lavoro W
 assorbe il calore Q2 dal serbatoio più freddo
 cede la quantità di calore Q1 al serbatoio più
caldo
Abbiamo realizzato un frigorifero
Si definisce coefficiente di prestazione del
frigorifero
w
Qass

W
9
Irreversibilità e II principio
le trasformazioni in natura sono irreversibili!!! Procedono in
un’unica direzione.
 per es. due corpi a temperatura differente: il calore può passare da
quello più caldo a quello più freddo ma non il viceversa.
 Pendolo messo in oscillazione: parte dell’energia meccanica viene
ceduta sotto forma di energia interna dell’aria. Non può accadere il
viceversa.
Perché??  Il II principio della termodinamica
10
L’entropia
Esiste una funzione di stato l’ entropia, S:
tale che l’integrale del calore scambiato reversibilmente diviso per la
T a cui avviene lo scambio, tra lo stato i e lo stato f, è dato dalla
differenza dei valori della funzione S nello stato finale meno quello
dello stato iniziale.

i
R


f
QR
T
 S f  S i  S
La variazione di entropia non dipende dalla trasformazione, sia
reversibile o irreversibile.
Attenzione: il calcolo di S deve essere fatto SOLO su una
trasformazione REVESIBILE
11
L’entropia: funzione di stato
dQ  dL  dU
Gas perfetto
dQ  pdV  ncV dT
dQ
dV
dT
 nR
 ncV
T
V
T
f
f
f
dQ
dV
dT
i T  i nR V  ncV i T
S  nR ln
Vf
Vi
 ncV ln
Tf
Ti
Vale per qualunque
trasformazione tra i
ed f
12
Applicazioni



Consideriamo due corpi a T1 e T2: il calore ceduto dal corpo 1 ed
assorbito dal corpo 2, fino alla T di equilibrio.
La trasformazione è irreversibile.
Il calore trasferito da un corpo all’altro può essere calcolato come se la
trasformazione fosse reversibile È a pressione costante
T1>T2
T1
Q1
T2
Q1 m1c1 Tm  T1   0
Q2 m2c2 Tm  T2   0
Q2
Q2  Q1  0  m2c2 Tm  T2   m1c1 Tm  T1 
m1c1T1  m 2 c 2T2
Tm 
m 1c1  m 2c 2
13
Applicazioni
f
S1  
i
f
S 2  
i
QR
m
QR
m
Tm
m1c1dT

 m1c1 ln
T
T
T1
1
T
T
m2c2 dT
 m2c2 ln m
T
T2
2

Tm
Tm
S  S1  S 2  m1c1 ln
 m2 c2 ln
0
T1
T2
14
Applicazioni


L’espansione libera è una trasformazione irreversibile
Per calcolo la variazione dell’entropia dobbiamo
utilizzare trasformazione isoterma reversibile
dU  W  Q
f
S sist  
i
QR
T
f

dU  0  W  Q
QR
i
T
f
 
i
W
T
f

i
pdV

T
f
Vf
nRT dV

 nR ln
T V
Vi
i
Samb  0
Suniv  Ssist  Samb  0
15
Applicazioni
Cambiamento di fase:
S  Sliq  Ssol
liq
QR
1


sol Tfusion e la temperaturaTfusion e

di fusio ne è
costante
S 
m fusione
T fusione
liq
m fusion e
Q R 
Tfusion e
sol

0
16
Applicazioni
c
Per un trasformazione qualunque: poiché
l’entropia è una funzione di stato, possiamo
considerare una qualunque trasformazione
reversibile.
f
S  
i
QR
T
c

i
QR
T
f

c
QR
c
i
f
nCV dT
nRT dV



T
T
T V
i
c
f
Vf
Tc
dT
dV
  nCV
  nR
 nCV ln  nR ln
T c
V
Ti
Vc
i
c
f
Tf
V
 nR ln f
Ti
Vi
T
P
S  nCP ln f  nR ln f
Ti
Pi
P
V
S  nCV ln f  nCp ln f
Pi
Vi
S  nCV ln
17
Applicazioni
Universo
Trasformazione reversibile
dS sist 
Ambiente
Q
T
dS serb  
Serbatoio di calore
Q
Sistema
T
dSUniv.  dS Sist  dS Serb 
Q
T

Q
T
0
X es. spansione isoterma reversibile...
18
II principio della Termodinamica:
Enunciato I: se il sistema è isolato, l’entropia del sistema non
può diminuire, aumenta se la trasformazione è irreversibile;
resta costante se la trasformazione è reversibile.
Suniv  S sist  Samb  0
Ciclo irreversibile
Suniv  Samb  0
L’Universo è un sistema isolato
Ciclo reversibile
Suniv  Samb  0
L’irreversibilità è sempre accompagnata da un aumento
di entropia.!!
Ogni processo naturale evolve sempre nella direzione
verso cui aumenta l’entropia.
19
Le macchine termiche

Il I principio:
U  Q  W  0  Q  W
Calore può essere trasformato in lavoro meccanico.
 Un espansione isoterma trasforma tutto il Q in W
 Le macchine termiche sono sistemi termodinamici che descrivono un
ciclo. Una parte del ciclo assorbe calore da uno o più serbatoi, un’altra
parte cede calore a uno o più serbatoi.
 Esempi di macchine termiche: il motore dell’automobile, le locomotive a
vapore.
W
Qass  Qced
Qced


 1
 Il rendimento della macchina:
Q
Q
Q
ass
ass
ass
È possibile realizzare un processo il cui unico risultato
sia quello di assorbire calore da un serbatoio e di
convertirlo completamente in lavoro?? Q ceduto = 0
Macchina mono-terma
W(=Q1)
20
Enunciati II del 2° principio della Termodinamica
 Enunciato II (di Kelvin-Planck): è
impossibile realizzare un processo che abbia
come unico risultato la trasformazione in
lavoro del calore fornito da una sorgente a
temperatura uniforme.
non esiste la macchina monoterma ossia la
macchina perfetta!!!.
dS macchina  0
dS serb
Q
 0
T
Suniv  0 assurdo!!!
21
Enunciato III del II principio della Termodinamica
 Enunciato III (di Clausius): è impossibile
realizzare un processo che abbia come unico
risultato il trasferimento di una quantità di calore da
un corpo ad un altro a temperatura maggiore.
SERVE W non esiste il frigorifero perfetto!!
dS macchina  0
dS serb
Q Q
 
T2 T1
T1  T2  dS serb  0
Suniv  0 assurdo!!!
22
Riassumiamo II principio
Enunciato I: se il sistema è isolato, l’entropia del sistema non
può diminuire, aumenta se la trasformazione è irreversibile; resta
costante se la trasformazione è reversibile.
 Enunciato II (di Kelvin-Planck): è impossibile realizzare un
processo che abbia come unico risultato la trasformazione in
lavoro del calore fornito da una sorgente a temperatura uniforme
 Enunciato III (di Clausius): è impossibile realizzare un
processo che abbia come unico risultato il trasferimento di una
quantità di calore da un corpo ad un altro a temperatura maggiore.
23
Equivalenza degli enunciati II e III
 Dimostriamo che la violazione di uno implichi
la violazione dell’altro. Violato enunciato II
Q1,C
 Supponiamo che esista una macchina termica 1
che trasformi tutto il calore il lavoro.
Q2 , C
W  Q1
 Prendiamo un’altra macchina di Carnot 2) che
lavori come frigorifero.
 Macchina complessiva:
Cede
Assorbe
Q1,C  Q2,C  W
Q2,C
Q1,C  Q1  Q1,C  W  Q2,C
24
Il teorema di Carnot


Tutte le macchine che lavorano tra due termostati
hanno un rendimento che è minore, o al massimo
uguale, a quello di una macchina di Carnot che
lavori tra gli stessi due termostati.
tutte le macchine reversibili (tutte le macchine di
Carnot) che lavorano tra gli stessi termostati hanno,
tutte, lo stesso rendimento.
25
Il teorema di Carnot
La dimostrazione per assurdo:
 Supponiamo che esista una macchina X che lavori tra i due
termostati T1 e T2 che abbia un rendimento > della macchina di
Carnot operante come macchina frigorifera tra gli stessi termostati.
 Sia W il lavoro delle due macchine in un ciclo uguale
X 
Wtot
Q1, X
C 
T1
Wtot
Q1,C
Combiniamo le due macchine in
una sola macchina, non si compie
lavoro esterno.
Q1, X
Q1,C
Q2, X
Q2 , C
T2
Il teorema di Carnot
Assunto
 x  C 
Wtot
Q1, X

Wtot
Q1,C
 Q1,C  Q1, X
Wtot  Q1,C  Q2,C  Q1, X  Q2, X
Q1,C  Q1, X  Q2,C  Q2, X  Q  0
 Q1,C  Q1, X  Q  0
Q2,C  Q2, X  Q  0
OSSIA
Il teorema di Carnot
Combiniamo le due macchine in una sola macchina,
non si compie lavoro esterno.
T1
Q1, X
Q1,C
 Q1,C  Q1, X  Q  0
28
Q2, X
Q2 , C
T2
Q2,C  Q2, X  Q  0
Il calore viene trasferito dal serbatoio T1 a temperatura più
bassa a quello T2 a temperatura più alta senza che venga fatto
lavoro: contraddice il II principio della termodinamica!!
28