SCHEDE SUL CALCOLO NUMERICO

SCHEDE ED ESERCIZI SUL CALCOLO NUMERICO
Nel seguito si illustrano tre metodi per calcolare la soluzione approssimata a piacere di
un’equazione anche nei casi in cui non si dispone di una formula esplicita: il metodo di bisezione, il
metodo del punto fisso e il metodo di Newton (o delle tangenti). Tutti questi metodi sono fondati su
calcoli iterativi.
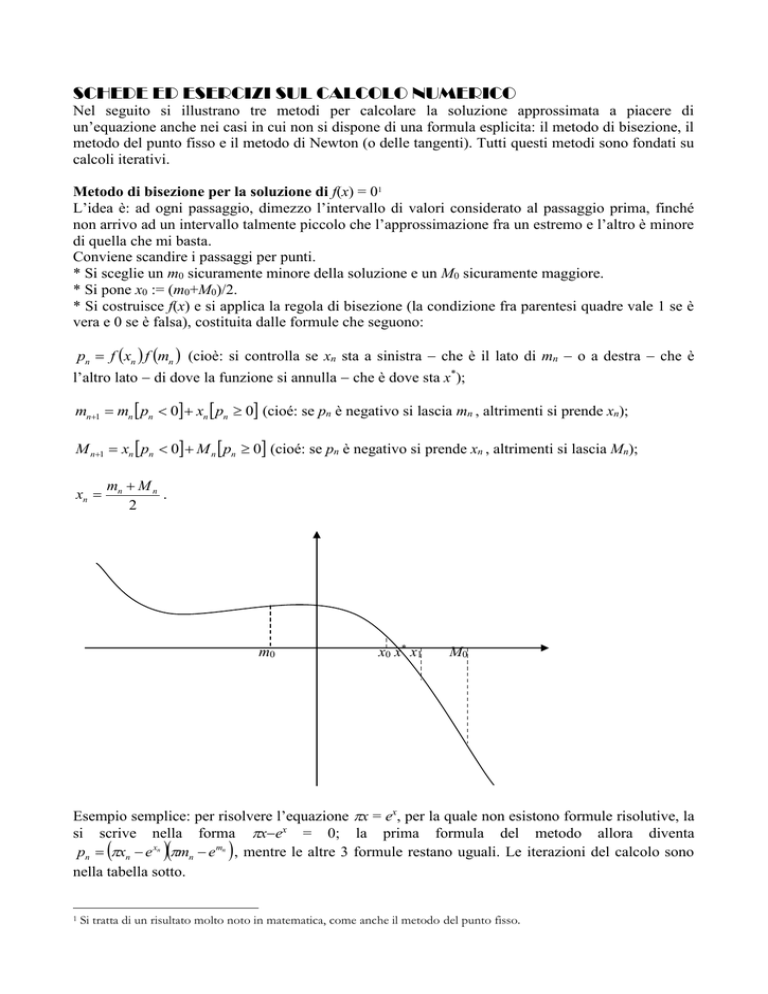
Metodo di bisezione per la soluzione di f(x) = 01
L’idea è: ad ogni passaggio, dimezzo l’intervallo di valori considerato al passaggio prima, finché
non arrivo ad un intervallo talmente piccolo che l’approssimazione fra un estremo e l’altro è minore
di quella che mi basta.
Conviene scandire i passaggi per punti.
* Si sceglie un m0 sicuramente minore della soluzione e un M0 sicuramente maggiore.
* Si pone x0 := (m0+M0)/2.
* Si costruisce f(x) e si applica la regola di bisezione (la condizione fra parentesi quadre vale 1 se è
vera e 0 se è falsa), costituita dalle formule che seguono:
pn  f xn  f mn  (cioè: si controlla se xn sta a sinistra  che è il lato di mn  o a destra  che è
l’altro lato  di dove la funzione si annulla  che è dove sta x*);
mn1  mn  pn  0  xn  pn  0 (cioé: se pn è negativo si lascia mn , altrimenti si prende xn);
M n1  xn  pn  0  M n  pn  0 (cioé: se pn è negativo si prende xn , altrimenti si lascia Mn);
xn 
mn  M n
.
2
m0
x0 x* x1
M0
Esempio semplice: per risolvere l’equazione x = ex, per la quale non esistono formule risolutive, la
si scrive nella forma xex = 0; la prima formula del metodo allora diventa
pn  xn  e xn mn  e mn , mentre le altre 3 formule restano uguali. Le iterazioni del calcolo sono
nella tabella sotto.

1


Si tratta di un risultato molto noto in matematica, come anche il metodo del punto fisso.
n
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
mn
0 (input)
0,5
0,5
0,5
0,5
0,53125
0,546875
0,546875
0,550781
0,552734
0,553711
0,553711
0,553711
0,553711
0,553772
0,553802
0,553818
0,553825
0,553825
0,553825
0,553826
0,553827
0,553827
0,553827
0,553827
Mn
1 (input)
1
0,75
0,625
0,5625
0,5625
0,5625
0,554688
0,554688
0,554688
0,554688
0,554199
0,553955
0,553833
0,553833
0,553833
0,553833
0,553833
0,553829
0,553827
0,553827
0,553827
0,553827
0,553827
0,553827
xn
0,5
0,75
0,625
0,5625
0,53125
0,546875
0,554688
0,550781
0,552734
0,553711
0,554199
0,553955
0,553833
0,553772
0,553802
0,553818
0,553825
0,553829
0,553827
0,553826
0,553827
0,553827
0,553827
0,553827
0,553827
f(xn)
-0,07792
0,239194
0,095249
0,012091
-0,03209
-0,00979
0,001205
-0,00428
-0,00153
-0,00016
0,000522
0,000179
8,37E-06
-7,7E-05
-3,4E-05
-1,3E-05
-2,3E-06
3,02E-06
3,49E-07
-9,9E-07
-3,2E-07
1,5E-08
-1,5E-07
-6,9E-08
-2,7E-08
f(mn)
-1
-0,07792
-0,07792
-0,07792
-0,07792
-0,03209
-0,00979
-0,00979
-0,00428
-0,00153
-0,00016
-0,00016
-0,00016
-0,00016
-7,7E-05
-3,4E-05
-1,3E-05
-2,3E-06
-2,3E-06
-2,3E-06
-9,9E-07
-3,2E-07
-3,2E-07
-1,5E-07
-6,9E-08
pn
0,077925
-0,01864
-0,00742
-0,00094
0,0025
0,000314
-1,2E-05
4,19E-05
6,56E-06
2,49E-07
-8,5E-08
-2,9E-08
-1,4E-09
1,26E-08
2,66E-09
4,48E-10
3,03E-11
-7E-12
-8,1E-13
2,3E-12
3,15E-13
-4,8E-15
4,85E-14
1,04E-14
1,83E-15
Criterio di
arresto
generale (w
= 1E-07)
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
TRUE
TRUE
Criterio di
arresto
bisezione
(w = 1E07)
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
TRUE
Esempio pratico: si conosce il capitale C e la rata costante P di un prestito, oltre che la sua durata in
periodi T; si vuole trovare il tasso periodico r. La formula che lega queste grandezze è nota dalla
1
1
1  r T . In questo caso, l’incognita è r, che non può in generale
matematica finanziaria: C  P
r
essere trovata con una formula esplicita, come dimostrato da Galois. Si può allora applicare il
1
1
1  r T  C  0 , per cui la prima formula del metodo di
metodo di bisezione all’equazione P
r
1
1

 

 1  1  x T
  1  1  m T

n
n
bisezione diventa pn   P
 C   P
 C  , mentre le altre 3 restano uguali.
xn
mn

 


 

Le iterazioni del calcolo sono nella tabella sotto.
n
0
mn
Mn
0,0000001 (input) 1 (input)
xn
0,5
f(xn)
-4600
Criterio di
arresto
generale
(w = 1Ef(mn)
pn
07)
2999,984 -1,4E+07 FALSE
Criterio di
arresto
bisezione
(w = 1E07)
FALSE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
0,0000001
0,0000001
0,0000001
0,0000001
0,0000001
0,0156251
0,0234376
0,0234376
0,0234376
0,0244142
0,0249024
0,0251466
0,0251466
0,0252076
0,0252381
0,0252381
0,0252381
0,0252419
0,0252419
0,0252429
0,0252434
0,0252436
0,0252437
0,0252438
0,5
0,25
0,125
0,0625
0,03125
0,03125
0,03125
0,027344
0,025391
0,025391
0,025391
0,025391
0,025269
0,025269
0,025269
0,025253
0,025246
0,025246
0,025244
0,025244
0,025244
0,025244
0,025244
0,025244
0,25
0,125
0,0625
0,03125
0,015625
0,023438
0,027344
0,025391
0,024414
0,024902
0,025147
0,025269
0,025208
0,025238
0,025253
0,025246
0,025242
0,025244
0,025243
0,025243
0,025244
0,025244
0,025244
0,025244
-4200,11
-3414,39
-2083,14
-469,06
915,4536
155,2779
-171,948
-12,3203
70,45323
28,81378
8,184012
-2,08379
3,0462
0,480229
-0,80202
-0,16096
0,15962
-0,00067
0,079472
0,039399
0,019363
0,009345
0,004336
0,001831
2999,984
2999,984
2999,984
2999,984
2999,984
915,4536
155,2779
155,2779
155,2779
70,45323
28,81378
8,184012
8,184012
3,0462
0,480229
0,480229
0,480229
0,15962
0,15962
0,079472
0,039399
0,019363
0,009345
0,004336
-1,3E+07
-1E+07
-6249379
-1407171
2746346
142149,7
-26699,7
-1913,08
10939,83
2030,024
235,8123
-17,0537
24,93013
1,462873
-0,38515
-0,0773
0,076654
-0,00011
0,012685
0,003131
0,000763
0,000181
4,05E-05
7,94E-06
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
TRUE
TRUE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
TRUE
Metodo del punto fisso per la soluzione di x = g(x)
L’idea è: ad ogni passaggio, uso la soluzione provvisoria che ho trovato nel passaggio precedente
per trovarne una ancora meglio approssimata.
La soluzione x* di un’equazione della forma x = g(x) si trova con l’iterazione
xn+1 = g(xn),
se è |g’(x*)| < 1 in un intorno di x* che contenga anche x0 .
xn+1
xn+1 = xn
xn+1 = g(xn)
x*
x* x2
x1
x0
xn
Esempio semplice: si riprende l’equazione x = ex, scrivendola come x = ex/. La derivata del
membro destro in x è se stesso. Non è evidente quale valore assuma l’espressione ex*/, ma si può
tentare il calcolo dell’iterazione xn+1 = exn/. Le iterazioni del calcolo sono nella tabella sotto.
n
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
xn
0 (input)
0,31831
0,437613
0,493064
0,521177
0,536036
0,544061
0,548445
0,550854
0,552183
0,552917
0,553323
0,553548
0,553673
0,553742
0,55378
0,553801
0,553813
0,553819
0,553823
0,553825
0,553826
0,553826
0,553827
0,553827
0,553827
0,553827
Criterio di
arresto (w
= 1E-07)
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
FALSE
TRUE
Un esame puramente visivo qui dà un risultato ingannevole; infatti le iterazioni 21 e 22 appaiono
uguali. Più avanti si spiegherà come stabilire un criterio di arresto delle iterazioni.
Esempio pratico: riprendendo il caso di un prestito a rate costanti, conviene scrivere l’equazione
/
P 
1 
P
T
P
1 
nella forma r  1 
. Il calcolo funziona perché si ha  1 
.

T 
T 1
T 
C  1  r  
 C  1  r    C 1  r 
Questa derivata vicino a r* è di sicuro minore di 1; infatti, sostituendo
1
1
T
T

1  r*  1

1 r* 
nella derivata, si ottiene (omettendo per semplicità l’asterisco,
CP
P
T
r*
r * 1  r * 
PT
che andrebbe indicato per ogni occorrenza di r)
; semplificando, si ha
T

1  r  1
T 1
1  r 
P
T
r 1  r 
1  r   1 , com’è noto dalla matematica finanziaria, si può
T
. L’espressione
T
r
1  r   1 1  r 
r
ottenere come somma di T termini della forma (1+r)t, ciascuno dei quali quindi è maggiore di 1.
T
T
 1 . Per giunta, il denominatore della derivata è
1  r T  1
r
moltiplicato per 1+r, che è un ulteriore elemento a favore della tesi.
Si può quindi trovare il punto fisso, cioè il tasso periodico di un prestito a rate costanti, con
P
1 
l’iterazione xn1  1 
 . Le iterazioni del calcolo sono nella tabella sotto.
C  1  xn T 
Basterebbe questo per stabilire che è
n
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Criterio di
arresto (w
xn
= 1E-07)
0,001 (input) FALSE
0,001568
FALSE
0,002429
FALSE
0,0037
FALSE
0,005493
FALSE
0,007871
FALSE
0,010768
FALSE
0,013938
FALSE
0,017007
FALSE
0,019625
FALSE
0,021616
FALSE
0,022996
FALSE
0,02389
FALSE
0,024443
FALSE
0,024775
FALSE
0,024971
FALSE
0,025086
FALSE
0,025153
FALSE
0,025191
FALSE
0,025214
FALSE
0,025226
FALSE
0,025234
FALSE
0,025238
FALSE
0,025241
FALSE
0,025242
FALSE
0,025243
FALSE
0,025243
FALSE
0,025243
FALSE
0,025244
TRUE
0,025244
Un punto fisso interessante in economia: il teorema della ragnatela
Un produttore mette un nuovo prodotto sul mercato e all’inizio stabilisce un prezzo p0.
La domanda inversa è descritta da pn = axn+b (pn è il prezzo unitario, xn è la quantità domandata),
pertanto la domanda diretta è descritta da xn = (bpn)/a e la quantità domandata è x0.
L’offerta è descritta da pn+1 = cxn+d, pertanto il produttore stabilisce un nuovo prezzo p1.
Al prezzo p1, la quantità domandata è x1.
Con una domanda x1, il prezzo è p2 .
Al prezzo p2, la quantità domandata è x2 .
Con una domanda x2, il prezzo è p3 e così via.
Tutto ciò è tanto naturale quanto concettualmente disordinato; ecco come sistemare i concetti.
* Da pn+1 = cxn+d e xn = (bpn)/a, si ottiene pn+1 = c(bpn)/a+d, cioè pn+1 = c/apn+(ad+bc)/a.
* Ponendo per semplicità di notazione m = c/a e q = (ad+bc)/a, si ottiene pn+1 = mpn+q. La
condizione |g’(x*)| < 1 qui è |m| < 1 cioè, dato che naturalmente a, b, c e d sono positivi, c/a < 1,
cioè c < a; ma si possono ottenere altre informazioni, come mostra il seguito.
* Il prezzo p0 è dato.
* Il prezzo p1 dipende da p0; infatti è p1 = mp0+q.
* Anche il prezzo p2 dipende da p0; infatti è p2 = mp1+q = m(mp0+q)+q = m2p0+q+mq.
* Anche il prezzo p3 dipende da p0; infatti è p3 = mp2+q = m(m2p0+q+mq)+q = m3p0+q+mq+m2q.
* In generale, qualunque prezzo pn dipende da p0; infatti è pn = mpn1+q =
m(mn1p0+q+mq+...+mn2q)+q = mnp0+q+mq+m2q+...+mn1q.
* Mediante la formula delle progressioni geometriche, si ottiene pn = mnp0+q(1mn)/(1m).
* Con 1 < m < 1 si ha m = 0, ma con m < 1 o m > 1 si ha m = .
* Quindi, con m “grande” il prezzo diverge fino a infinito e non c’è equilibrio di mercato, mentre
con m “piccolo” il prezzo di mercato c’è ed è q/(1m).
* Dato che è m = c/a, la condizione di m “piccolo” è 1 < c/a, cioè c/a < 1, cioè c < a; nient’altro
che la condizione per il punto fisso già determinata in precedenza. In altri termini, offerta e
domanda trovano un equilibrio se la capacità di adattamento c dell’offerta è meno reattiva della
capacità di adattamento a della domanda.
p
offerta (p = cx+d)
domanda (p = ax+b)
x
Metodo di Newton2
L’idea è la stessa del punto fisso, ma l’algoritmo è più efficiente.
Si dà direttamente la formula da applicare ad un’equazione nella forma f(x) = 0:
xn1  xn 
f  xn 
.
f /  xn 
Si tratta di un caso particolare di punto fisso, in cui la funzione g(x) assume la forma xf(x)/f’(x). La
 f x   f x  f x   1 , cioè f x  f x   1 .
condizione di convergenza è quindi 1 
 f x 
 f x 
/
* 2
*
/
* 2
//
*
*
/
//
*
* 2
Esempio semplice: riprendendo l’equazione x = ex, la si scrive come xex = 0. La derivata in x del
membro sinistro è ex, pertanto l’iterazione è data da
Introdotto da Newton in De analysi per aequationes numero terminorum infinitas, pubblicato nel 1711, disponibile in
http://www.e-rara.ch/zut/content/pageview/637329.
2

 

1  xn
x  e x
x*  e x  e x
. La condizione di convergenza è
xn1  xn  n x , cioè xn1 
 1 , cioè
2

x
 e
 e
1
x
n
n
e
n
*

*
*
*
e
ex

e x  x*  1 . Non è evidente se la condizione sia valida. Le iterazioni del calcolo sono
*
2

nella tabella sotto.
*
x
n
0
1
2
3
4
5
xn
0 (input)
0,466942
0,549819
0,553817
0,553827
0,553827
Criterio di
arresto (w
= 1E-07)
FALSE
FALSE
FALSE
FALSE
TRUE
Risulta subito evidente l’efficienza del metodo.
Esempio pratico: riprendendo ancora il prestito a rate costanti, risulta f r   P
1
1
1  r T  C  0 ,
r


T
1
1
quindi si ha f / r   P 
 2 2
 1  0 ; la formula di iterazione è dunque
T 1
T 
r




r
1

r
r
1

r


1
C
1
 xn
T
P

1  xn 
. Si tralascia il calcolo della condizione di
xn1  xn 
T
1
1
1
 
x
1  xn T 1 xn xn 1  xn T n P
convergenza. Le iterazioni del calcolo sono nella tabella sotto; data la pesantezza della formula, è
opportuno calcolare anche le celle d’appoggio per 1+xn e (1+xn)T.
n
0
1
2
3
4
5
xn
0,0001 (input)
0,018344
0,02467
0,02524
0,025244
0,025244
1+xn
1,0001
1,018344
1,02467
1,02524
1,025244
1,025244
(1+xn)T
0,996008
0,483309
0,377254
0,368963
0,368904
0,368904
Criterio di
arresto (w
= 1E-07)
FALSE
FALSE
FALSE
FALSE
TRUE
Criteri di arresto del calcolo
Il processo iterativo si arresta non appena si ha |xn+1xn| < w, dove w è piccolo a piacere, che
stabilisce l’errore tollerabile per chi esegue il calcolo; il senso è che, se due iterazioni di seguito
hanno valori molto vicini, allora anche continuando l’iterazione i miglioramenti
nell’approssimazione saranno trascurabili.
Indicando con en = x*xn la distanza fra la soluzione esatta e l’approssimazione n-esima, si dimostra
(Quarteroni, Sacco & Saleri [2004], Matematica numerica, Springer, pagg. 216-217) che è
1
xn1  xn  , perciò il criterio vale poco se g’(x*) è vicina a 1 (e quindi se en è molto
1  g / x*
maggiore di xn+1xn), mentre funziona molto bene per metodi di ordine 2 in cui si abbia g’(x*) = 0
(come quello di Newton); il criterio resta soddisfacente quando è 1 < g’(x*) < 0.
Per il metodo di bisezione esiste anche un criterio spontaneo: il calcolo può venire interrotto quando
si arriva a |mnMn| < w. Questo criterio, tuttavia, è più esigente di quello generale.
en 
 
Esercizi
1) Calcola i primi 3 passaggi per trovare almeno una soluzione col metodo di bisezione nelle
seguenti equazioni.
a) 6x = 5x
(è x* = 4,999871)
d) 5(x3) = x
(è x* = 1,34129)
Usa m0 = 2 e M0 = 5; trova x3 = 4,8125.
Usa m0 = 2 e M0 = 1; trova x3 = 1,3125.
b) log7x = x4
(è x* = 4,806841)
Usa m0 = 1 e M0 = 5; trova x3 = 4,75.
e) 3x 7 = lnx
(è x* = 1,847773)
Usa m0 = 0,5 e M0 = 5; trova x3 = 1,90625.
c) x7x5+x+7 = 0
(è x* = 1,41228)
Usa m0 = 3 e M0 = 3; trova x3 = 1,125.
f) 2x = x2
(è x* = 0,76666; e x* = 2...)
Usa m0 = 2 e M0 = 2; trova x3 = 0,75.
2) Calcola i primi 3 passaggi per trovare almeno una soluzione col metodo del punto fisso nelle
seguenti equazioni.
a) 6x = 5x
d) 5(x3) = x
Usa x0 = 2; trova x3 = 4,999871.
Usa x0 = 0; trova x3 = 1,34093.
b) log7x = x4
Usa x0 = 3; trova x3 = 4,803992.
e) 3x 7 = lnx
Usa x0 = 1; trova x3 = 0,002486.
c) x7x5+x+7 = 0
Usa x0 = 1,4; trova x3 = 2,6E+11.
f) 2x = x2
Usa x0 = 3; trova x3 = 3,470089.
3) Calcola i primi 3 passaggi per trovare almeno una soluzione col metodo di Newton nelle seguenti
equazioni.
a) 6x = 5x
d) 5(x3) = x
Usa x0 = 5; trova x3 = 3,326813.
Usa x0 = 4; trova x3 = #NUM!.
b) log7x = x4
Usa x0 = 2; trova x3 = 4,806841.
e) 3x 7 = lnx
Usa x0 = 1; trova x3 = 1,905302.
c) x7x5+x+7 = 0
Usa x0 = 0; trova x3 = 5,15487.
f) 2x = x2
Usa x0 = 0; trova x3 = 0,77347.