Diffrazione da una fenditura

Corso di Ottica con Laboratorio
A. A. 2015 – 2016
F. Somma, M. Barbieri
Esperienza 4
Oggetto: Verifica della legge della distribuzione dell’intensità nella diffrazione da fenditura
singola
Materiale a disposizione:
Banco ottico,sorgente laser a diodo, rivelatore di luce montato su slitta, metro a rollina, disco con
fenditure singole rettangolari e circolari di diversa dimensione, sistema di acquisizione dati on-line.
1.ASPETTI TEORICI
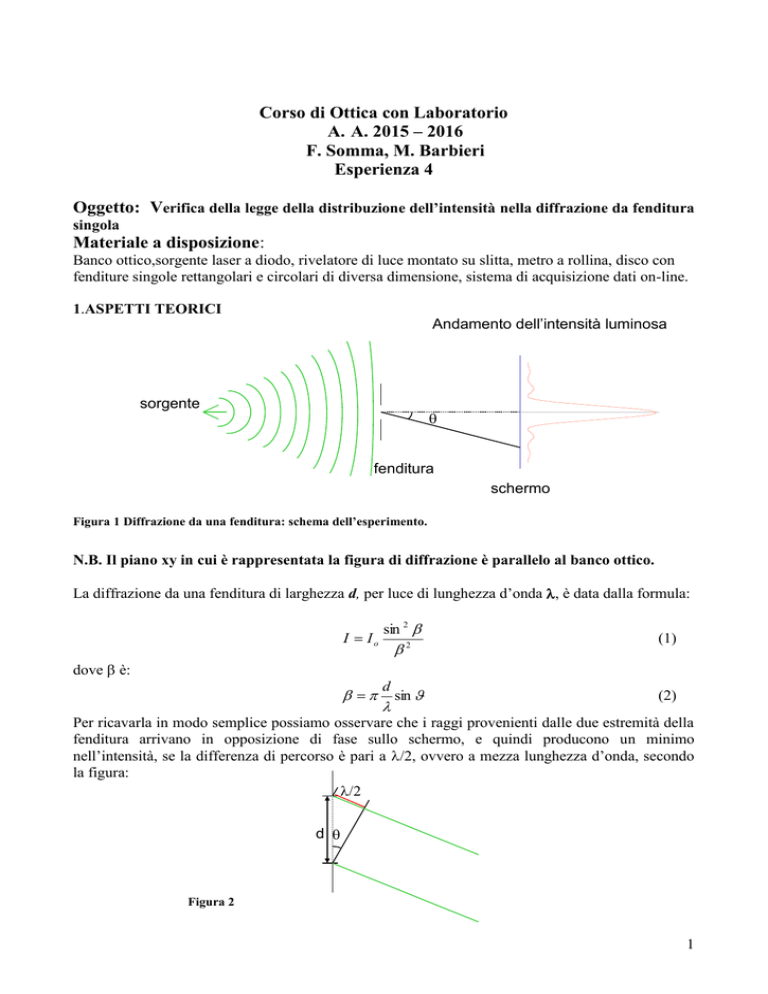
Andamento dell’intensità luminosa
sorgente

fenditura
schermo
Figura 1 Diffrazione da una fenditura: schema dell’esperimento.
N.B. Il piano xy in cui è rappresentata la figura di diffrazione è parallelo al banco ottico.
La diffrazione da una fenditura di larghezza d, per luce di lunghezza d’onda , è data dalla formula:
I  Io
sin 2 
2
(1)
dove  è:
 
d
sin 
(2)

Per ricavarla in modo semplice possiamo osservare che i raggi provenienti dalle due estremità della
fenditura arrivano in opposizione di fase sullo schermo, e quindi producono un minimo
nell’intensità, se la differenza di percorso è pari a /2, ovvero a mezza lunghezza d’onda, secondo
la figura:

d 
Figura 2
1
In realtà, a causa del contributo di tutti i punti interni alla fenditura i minimi dell’intensità si hanno
per una differenza di percorso tra i due raggi provenienti dai punti estremi pari a n.
d sen= n  con n, ordine del minimo, numero intero positivo o negativo.
d/2


Figura 3
Infatti la costruzione geometrica, considerando coppie di punti distanti d/2 ci porta alla semplice
formula:
d


sin  
da cui d sin    ovvero sin  
2
2
d
I minimi di intensità nella (1) si hanno per
   ,2 ,3 ...
ovvero per
d
 sin    n

cioè:



sin    ,2 ,3 .....
d
d
d
(3)
(4)
(5)
(6)
Supponiamo di osservare la figura di diffrazione su uno schermo distante L dalla fenditura,
definiamo X la distanza misurata sullo schermo tra il centro del massimo centrale e uno dei minimi
di diffrazione, e  l’angolo formato dalla congiungente il centro della fenditura con il minimo
osservato (Figura 4).
d

L
X
Figura 4
Vale la relazione
tan   X / L
(7)
Poiché l’angolo è piccolo possiamo approssimare la funzione tan con la funzione sen e scrivere
che, usando la (6), i minimi nella figura di diffrazione si avranno quando:
X


(8)
senn  tan  n  n   ,2 ,.....
L
d
d
2
Dall’esperimento possiamo misurare la posizione Xn dei diversi minimi, calcolare Xn/L e ricavare
/d. Nota la lunghezza d’onda  della luce utilizzata, possiamo ricavare la larghezza d della
fenditura .
.
Scopo dell’esperienza: determinare la forma della figura di diffrazione e misurare la
larghezza d della fenditura .
Descrizione dell’esperienza:
Montare gli strumenti sul banco ottico secondo lo schema della figura 5
Figura 5
Figura 6
Ci si assicuri che il rivelatore di luce sia allineato sul massimo centrale della figura di
diffrazione in modo da posizionarlo al centro della frangia rispetto sia alla direzione verticale
che a quella orizzontale. In corrispondenza di questa posizione il movimento orizzontale, che ci
dà la misura di X,deve essere posto a metà corsa per ottenere un’escursione simmetrica rispetto
al massimo centrale sinX = 
3
Dal rivelatore il segnale luminoso viene inviato tramite interfaccia al PC, che utilizzando il
programma DATA-STUDIO, permette di analizzare per punti la figura di diffrazione e
disegnare il grafico dell’andamento sperimentale dell’intensità I/Imax in funzione della
posizione lineare X.
Spostando il rivelatore manualmente e lentamente si incontreranno tutte le frange di diffrazione
prodotte e contemporaneamente sullo schermo del PC comparirà un grafico con massimi e
minimi secondari (fig.6) che riprodurrà una figura di diffrazione (fig.6 superiore)
corrispondente alla funzione data dall’equazione (1).
Si riporteranno in una tabella i valori delle posizioni Xn(mm) dei minimi ai vari ordini
individuate con il puntatore direttamente dal grafico.
Per ottenete con maggior precisione la posizione dei minimi Xn± per ogni valore di n, si calcoli
la semidistanza tra due minimi laterali corrispondenti a ± n rispetto al massimo centrale:
1
X  X n  X n 
2
Utilizzando i dati ricavati con la (8) si riporta in grafico sinin funzione di n, ordine del
minimo, e mediante la procedura della regressione lineare si ricavi il coefficiente angolare e
quindi, nota, si determini la larghezza d della fenditura con la sua incertezza d
Quesiti
Si ripetano le operazioni di misura della figura di diffrazione, sopra descritta, per almeno tre
fenditure di larghezza diversa; dal confronto dei grafici di discuta quale relazione intercorre tra
la larghezza d della fenditura singola e la forma del massimo principale e dei massimi
secondari, e la loro distanza relativa.
Commenti e riflessioni sui risultati ottenuti.
.
4