Campo ideale dei PF Coils di Multi-Pinch
(Accuratezza richiesta)
Le quattro bobine di campo poloidale dell’esperimento Multi-Pinch (PF2, PF3.1,
PF4.1, PF4.2) vanno valutate a coppie, ad esempio il campo magnetico di ogni bobina
va inteso come prodotto da una coppia di bobine identiche posizionate con asse di
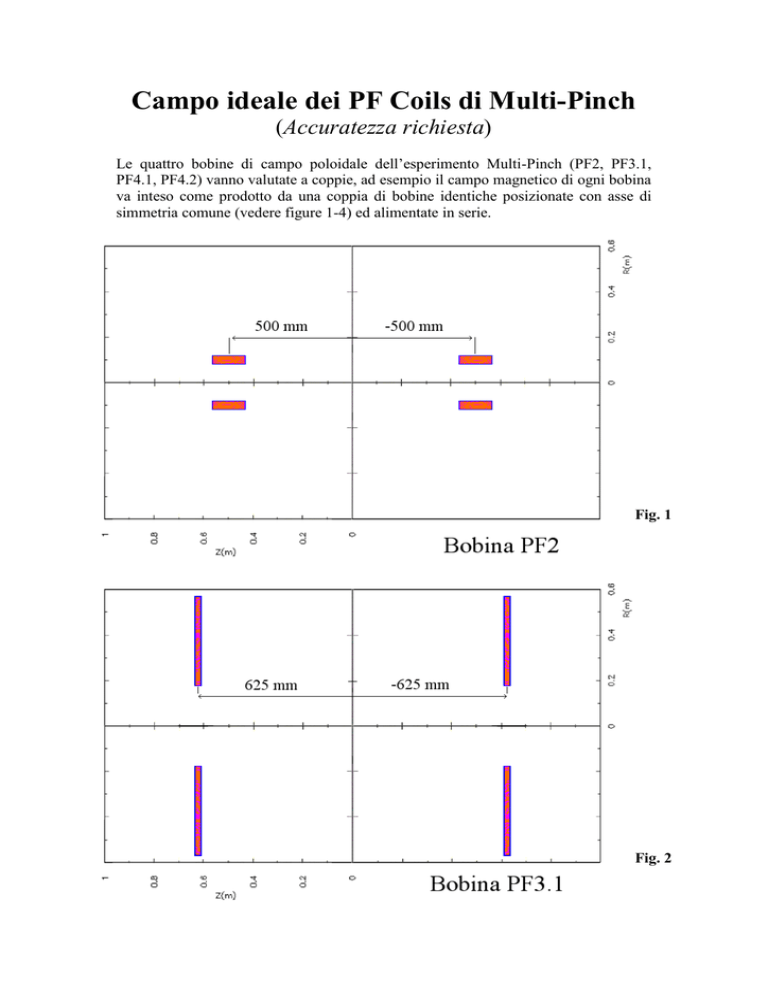
simmetria comune (vedere figure 1-4) ed alimentate in serie.
Fig. 1
Fig. 2
Fig. 3
Fig. 4
2
PF2 (1875 A per spira, 48 spire)
(posizione del baricentro delle due bobine: Z = ±500 mm)
Campo magnetico ideale a (R = 400 mm, Z = 0 mm):
(BR,BZ) = ( 0 , 18.29 ) [Gauss].
Il valore del campo BZ deve discrepare per meno di ±8 [Gauss] da quello ideale su di
una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo toroidale
(coordinate cilindriche R,,Z). Il campo BR deve essere ≤1% di BZ sugli stessi punti.
Campo magnetico ideale a (R = 200 mm, Z = ±200 mm):
(BR,BZ) = ( -/+75.19 , 79.76 ) [Gauss].
Il valore dei campi (BR,BZ) deve discrepare per meno di (±11, ±7) [Gauss] da quello
ideale su di una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo
toroidale (coordinate cilindriche R,,Z).
Campo magnetico ideale a (R = 400 mm, Z = ±820 mm):
(BR,BZ) = ( +/-32.16 , 6.01 ) [Gauss].
Il valore dei campi (BR,BZ) deve discrepare per meno di (±6, ±0.2) [Gauss] da quello
ideale su di una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo
toroidale (coordinate cilindriche R,,Z).
Campo magnetico ideale sull’asse delle bobine (R = 0 mm), il valore del campo BZ
deve essere mantenuto entro un errore dell’1% e quello del campo BR deve essere
≤1% di BZ sugli stessi punti:
Z = 1000 mm (BR,BZ) = ( 0 , 46.13 ) [Gauss]
Z = 800 mm (BR,BZ) = ( 0 , 196.6 ) [Gauss]
Z = 600 mm (BR,BZ) = ( 0 , 2286 ) [Gauss]
Z = 400 mm (BR,BZ) = ( 0 , 2290 ) [Gauss]
Z = 200 mm (BR,BZ) = ( 0 , 210.5 ) [Gauss]
Z=
0 mm (BR,BZ) = ( 0 , 88.87 ) [Gauss]
Z = -200 mm (BR,BZ) = ( 0 , 210.5 ) [Gauss]
Z = -400 mm (BR,BZ) = ( 0 , 2290 ) [Gauss]
Z = -600 mm (BR,BZ) = ( 0 , 2286 ) [Gauss]
Z = -800 mm (BR,BZ) = ( 0 , 196.6 ) [Gauss]
Z = -1000 mm (BR,BZ) = ( 0 , 46.13 ) [Gauss]
3
PF3.1 (1875 A per spira, 24 spire)
(posizione del baricentro delle due bobine: Z = ±625 mm)
Campo magnetico ideale a (R = 400 mm, Z = 0 mm):
(BR,BZ) = ( 0 , 105.8 ) [Gauss].
Il valore del campo BZ deve discrepare per meno di ±8 [Gauss] da quello ideale su di
una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo toroidale
(coordinate cilindriche R,,Z). Il campo BR deve essere ≤1% di BZ sugli stessi punti.
Campo magnetico ideale a (R = 200 mm, Z = ±200 mm):
(BR,BZ) = ( -/+55.93 , 210.0 ) [Gauss].
Il valore dei campi (BR,BZ) deve discrepare per meno di (±11, ±7) [Gauss] da quello
ideale su di una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo
toroidale (coordinate cilindriche R,,Z).
Campo magnetico ideale a (R = 400 mm, Z = ±820 mm):
(BR,BZ) = ( +/-277.5 , 168.2 ) [Gauss].
Il valore dei campi (BR,BZ) deve discrepare per meno di (±6, ±0.2) [Gauss] da quello
ideale su di una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo
toroidale (coordinate cilindriche R,,Z).
Campo magnetico ideale sull’asse delle bobine (R = 0 mm), il valore del campo BZ
deve essere mantenuto entro un errore dell’1% e quello del campo BR deve essere
≤1% di BZ sugli stessi punti:
Z = 1000 mm (BR,BZ) = ( 0 , 250.5 ) [Gauss]
Z = 800 mm (BR,BZ) = ( 0 , 566.7 ) [Gauss]
Z = 600 mm (BR,BZ) = ( 0 , 874.0 ) [Gauss]
Z = 400 mm (BR,BZ) = ( 0 , 481.2 ) [Gauss]
Z = 200 mm (BR,BZ) = ( 0 , 248.9 ) [Gauss]
Z=
0 mm (BR,BZ) = ( 0 , 190.4 ) [Gauss]
Z = -200 mm (BR,BZ) = ( 0 , 248.9 ) [Gauss]
Z = -400 mm (BR,BZ) = ( 0 , 481.2 ) [Gauss]
Z = -600 mm (BR,BZ) = ( 0 , 874.0 ) [Gauss]
Z = -800 mm (BR,BZ) = ( 0 , 566.7 ) [Gauss]
Z = -1000 mm (BR,BZ) = ( 0 , 250.5 ) [Gauss]
4
PF4.1 (-1875 A per spira, 18 spire)
(posizione del baricentro delle due bobine: Z = ±885 mm)
Campo magnetico ideale a (R = 400 mm, Z = 0 mm):
(BR,BZ) = ( 0 , -3.85 ) [Gauss].
Il valore del campo BZ deve discrepare per meno di ±8 [Gauss] da quello ideale su di
una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo toroidale
(coordinate cilindriche R,,Z). Il campo BR deve essere ≤1% di BZ sugli stessi punti.
Campo magnetico ideale a (R = 200 mm, Z = ±200 mm):
(BR,BZ) = ( +/-2.02 , -7.3 ) [Gauss].
Il valore dei campi (BR,BZ) deve discrepare per meno di (±11, ±7) [Gauss] da quello
ideale su di una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo
toroidale (coordinate cilindriche R,,Z).
Campo magnetico ideale a (R = 400 mm, Z = ±820 mm):
(BR,BZ) = ( +/-10.04 , 17.69 ) [Gauss].
Il valore dei campi (BR,BZ) deve discrepare per meno di (±6, ±0.2) [Gauss] da quello
ideale su di una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo
toroidale (coordinate cilindriche R,,Z).
Campo magnetico ideale sull’asse delle bobine (R = 0 mm), il valore del campo BZ
deve essere mantenuto entro un errore dell’1% e quello del campo BR deve essere
≤1% di BZ sugli stessi punti:
Z = 1000 mm (BR,BZ) = ( 0 , -545.5 ) [Gauss]
Z = 800 mm (BR,BZ) = ( 0 , -845.0 ) [Gauss]
Z = 600 mm (BR,BZ) = ( 0 , -80.52 ) [Gauss]
Z = 400 mm (BR,BZ) = ( 0 , -20.12 ) [Gauss]
Z = 200 mm (BR,BZ) = ( 0 , -8.9 ) [Gauss]
Z=
0 mm (BR,BZ) = ( 0 , -6.7 ) [Gauss]
Z = -200 mm (BR,BZ) = ( 0 , -8.9 ) [Gauss]
Z = -400 mm (BR,BZ) = ( 0 , -20.12 ) [Gauss]
Z = -600 mm (BR,BZ) = ( 0 , -80.52 ) [Gauss]
Z = -800 mm (BR,BZ) = ( 0 , -845.0 ) [Gauss]
Z = -1000 mm (BR,BZ) = ( 0 , -545.5 ) [Gauss]
5
PF4.2 (-1875 A per spira, 18 spire)
(posizione del baricentro delle due bobine: Z = ±985 mm)
Campo magnetico ideale a (R = 400 mm, Z = 0 mm):
(BR,BZ) = ( 0 , -41.12 ) [Gauss].
Il valore del campo BZ deve discrepare per meno di ±8 [Gauss] da quello ideale su di
una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo toroidale
(coordinate cilindriche R,,Z). Il campo BR deve essere ≤1% di BZ sugli stessi punti.
Campo magnetico ideale a (R = 200 mm, Z = ±200 mm):
(BR,BZ) = ( +/-9.5 , -60.65 ) [Gauss].
Il valore dei campi (BR,BZ) deve discrepare per meno di (±11, ±7) [Gauss] da quello
ideale su di una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo
toroidale (coordinate cilindriche R,,Z).
Campo magnetico ideale a (R = 400 mm, Z = ±820 mm):
(BR,BZ) = ( +/-256.5 , -173.8 ) [Gauss].
Il valore dei campi (BR,BZ) deve discrepare per meno di (±6, ±0.2) [Gauss] da quello
ideale su di una circonferenza di diametro 2R in 12 punti equispaziati nell’angolo
toroidale (coordinate cilindriche R,,Z).
Campo magnetico ideale sull’asse delle bobine (R = 0 mm), il valore del campo BZ
deve essere mantenuto entro un errore dell’1% e quello del campo BR deve essere
≤1% di BZ sugli stessi punti:
Z = 1000 mm (BR,BZ) = ( 0 , -573.4 ) [Gauss]
Z = 800 mm (BR,BZ) = ( 0 , -369.6 ) [Gauss]
Z = 600 mm (BR,BZ) = ( 0 , -194.9 ) [Gauss]
Z = 400 mm (BR,BZ) = ( 0 , -103.3 ) [Gauss]
Z = 200 mm (BR,BZ) = ( 0 , -66.68 ) [Gauss]
Z=
0 mm (BR,BZ) = ( 0 , -56.87 ) [Gauss]
Z = -200 mm (BR,BZ) = ( 0 , -66.68 ) [Gauss]
Z = -400 mm (BR,BZ) = ( 0 , -103.3 ) [Gauss]
Z = -600 mm (BR,BZ) = ( 0 , -194.9 ) [Gauss]
Z = -800 mm (BR,BZ) = ( 0 , -369.6 ) [Gauss]
Z = -1000 mm (BR,BZ) = ( 0 , -573.4 ) [Gauss]
6












