SULLE SPALLE DEI GIGANTI. INTERROGARE LA REALTA' GUIDATI DA UN MAESTRO
TESINA DI RICERCA : “LA FUNZIONE SINUSOIDALE”
Il progetto enfatizza la ricerca della funzione sinusoidale per la rilevante importanza e diffusa
applicazione di questa funzione in campi molto diversi come la topografia, l'ottica, l'elettronica.
Partiamo dall’osservazione di fatti e fenomeni facilmente comprensibili utilizzando e modificando i
quadrilateri articolabili isoperimetrici non equivalenti.
In tali trasformazioni ci rendiamo conto che vi sono elementi che non cambiano (gli invarianti),
come la somma degli angoli, ed altri che cambiano nel passaggio da una figura all’altra come la
somma delle diagonali e l’area.
h
h
h
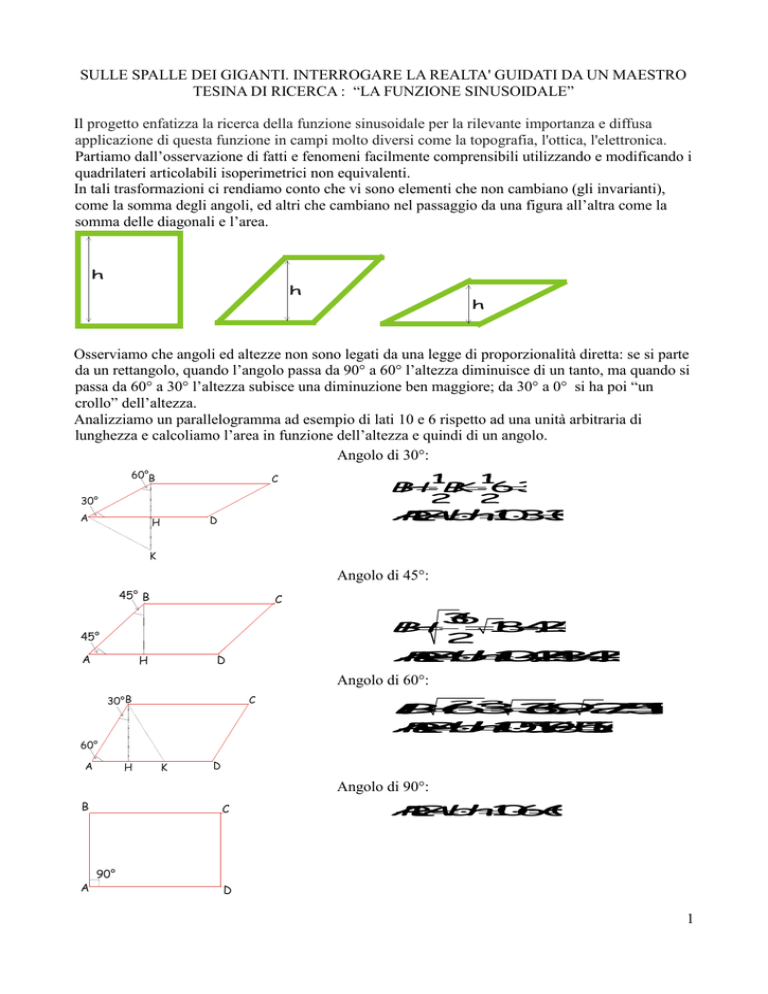
Osserviamo che angoli ed altezze non sono legati da una legge di proporzionalità diretta: se si parte
da un rettangolo, quando l’angolo passa da 90° a 60° l’altezza diminuisce di un tanto, ma quando si
passa da 60° a 30° l’altezza subisce una diminuzione ben maggiore; da 30° a 0° si ha poi “un
crollo” dell’altezza.
Analizziamo un parallelogramma ad esempio di lati 10 e 6 rispetto ad una unità arbitraria di
lunghezza e calcoliamo l’area in funzione dell’altezza e quindi di un angolo.
Angolo di 30°:
60°B
C
30°
A
D
H
1
1
B
H
B
K
63
2
2
A
R
E
A
b
h
1
0
3
3
0
K
Angolo di 45°:
45° B
C
3
6
1
8
4
.
2
4
3
2
A
R
E
A
b
h
1
0
4
.
2
4
3
4
2
.
4
3
B
H
45°
A
D
H
Angolo di 60°:
30° B
C
22
B
H
6
3
3
6
9
2
7
5
.
1
9
6
A
R
E
A
b
h
1
0
5
.
1
9
6
5
1
.
9
6
60°
A
H
K
D
Angolo di 90°:
B
A
C
A
R
E
A
b
h
1
0
6
6
0
90°
D
1
Facciamo la rappresentazione cartesiana nel sistema angolo-area.
Angolo x
0°
30°
45°
60°
90°
120°
135°
150°
180°
…
y
Area y
0
30
42.43
51.96
60
51.96
42.43
30
0
…
60
51.96
42.43
30
30°
45° 60°
90°
120° 135° 150°
180°
x
Unendo i punti che rappresentano le coppie ordinate (x,y) della tabella otteniamo una spezzata; i
punti appartengono ad un grafico chiamato sinusoide; per ottenere una curva continua dovremmo
calcolare l'area al variare continuo dell'angolo; sarà necessario considerare anche altezze negative e
quindi aree negative.
y
6
0
5
1
.9
6
4
2
.4
3
3
0
0
°
5
°6
3
0
° 4
9
0
°
5
0
°
3
5
°1
1
2
0
°1
1
8
0
°
2
5
°2
4
0
°
2
1
0
°2
2
7
0
°
1
5
°3
3
0
0
°3
3
0
°
x
3
6
0
°
3
0
4
2
.4
3
5
1
.9
6
6
0
La professoressa ci suggerisce la costruzione di un particolare dispositivo mobile per osservare
come, mentre un parallelogramma “avanza”, l’altezza “descrive” una sinusoide. Discutiamo sui
materiali da utilizzare e progettiamo la realizzazione con materiali semplici facendoci aiutare dal
babbo o da un artigiano.
r
a
b
2
L'impronta della sinusoide tracciata dall'altezza del parallelogramma
Due dischi di plexiglas di raggio r sono collegati tra loro da un listello di legno di lunghezza b
(uguale alla base del parallelogramma) imperniato ai loro centri insieme a due listelli di lunghezza a
che formano i lati minori del parallelogramma; alle altre due estremità di questi è collegato un
listello di lunghezza b, altro lato del parallelogramma, imperniato ai dischi in modo che la rotazione
di questi sia sincronizzata. Una guida mobile, spostata manualmente, fa ruotare il dispositivo sulla
guida sottostante. Nel punto medio del listello che collega i due centri dei dischi è fissato, in modo
ortogonale, un listello di lunghezza 2r. Durante la rotazione l'intersezione tra il listello ortogonale
fissato nella mezzeria e il listello periferico di collegamento dei due dischi descrive la sinusoide.
3
Il dispositivo mobile ci mostra che al variare dell'angolo, fra due lati consecutivi, varia l'altezza del
parallelogramma. Questa altezza descrive una curva che si chiama sinusoide e rappresenta il
grafico di una funzione periodica, infatti ogni 360° si ripetono gli stessi valori delle altezze. La
professoressa ci pone alcune domande chiedendoci se in natura esistono fenomeni caratterizzati dal
fatto di essere ripetitivi, ovvero di ricorrere sempre uguali nel tempo per una durata indefinita. Ci
vengono in mente alcuni moti oscillatori che abbiamo studiato in fisica l'anno precedente: quello
che si ottiene spostando e poi lasciando andare una massa attaccata ad una molla vincolata all'altro
estremo o lasciando cadere una pallina attaccata ad un elastico vincolato all'altro estremo.
Pizzicando la corda di una chitarra, un suo punto ripassa avanti e indietro rispetto alla posizione di
equilibrio; un pendolo appeso ad un filo descrive un arco a destra e a sinistra della sua verticale.
Cominciamo a progettare qualche semplice dispositivo oscillante che sia in grado, in certe
condizioni, di disegnare una “traccia” visibile del fenomeno periodico. Pensiamo al moto di una
penna solidale ad una massa che oscilla in un piano verticale - perché appesa ad una molla - e di un
foglio di carta che scorre ortogonalmente al piano di oscillazione a velocità costante. La punta della
penna, a contatto del foglio di carta, dovrebbe disegnare la sinusoide. Il modello ci sembra però
difficile da realizzare. A qualcuno viene in mente di costruire un pendolo che lascia la traccia.
Prendere un grosso imbuto e riempirlo di sabbia finissima; tramite due cordicelle appenderlo ad un
gancio, dare una piccola spinta e sotto l'imbuto far scorrere, ortogonalmente al piano delle
oscillazioni, un lungo foglio di carta. La sabbia che cade sul foglio disegnerà una traccia a forma di
onda, più o meno ampia, che dovrebbe essere una sinusoide. Decidiamo di costruire questo pendolo
reale facendoci aiutare, nella costruzione in legno, da un artigiano.
L'impronta della sinusoide lasciata dal pendolo
Una piccola tramoggia in legno, con foro di 2
mm, è appesa ad un sostegno, tramite due
doppie corde, ad una altezza di circa 60 cm.
Nella tramoggia, con il foro chiuso, viene
introdotta un po' di sabbia asciutta e setacciata.
4
Il foro sotto la tramoggia viene aperto e la
Il piano di base, manualmente, viene traslato in
stessa viene fatta oscillare su un piano
modo ortogonale all'oscillazione con velocità,
ortogonale a quello di base. La sabbia comincia per quanto possibile, costante.
a scendere.
La traccia della sabbia lasciata dal pendolo oscillante è una sinusoide.
5
Lo studio con il software Cabri
Al fine di disegnare la sinusoide utilizzando il software matematico 'Cabri II Plus 1.4.3' serve
conoscere la definizione di seno di un angolo :“Dato un qualsiasi angolo , di vertice O, preso
un punto P di un primo lato dell'angolo e condotta la proiezione H del punto P sull'altro lato
dell'angolo, considerato il triangolo rettangolo POH, il rapporto PH/OP è, per definizione, il seno
dell'angolo .” Si dimostra che tale rapporto è indipendente dal punto P scelto sul primo lato.
Analizziamo un parallelogramma ad esempio di lati 10 e 6 rispetto ad una unità arbitraria di
lunghezza e indichiamo con x l'ampiezza di un angolo, da 0° a 180°, che abbia il vertice in un
estremo della base di appoggio del parallelogramma e i cui lati siano: la semiretta di base orientata
verso destra e la semiretta di sostegno del lato obliquo snodabile. Conduciamo dal vertice opposto
alla base l'altezza ad essa relativa: si viene a formare un triangolo rettangolo i cui cateti sono
l'altezza e la proiezione del lato obliquo sulla base; l'ipotenusa è rappresentata dal lato obliquo del
parallelogramma. Ricordando la definizione di seno di un angolo, inversamente, si ricava l'altezza
data del seno dell'angolo che le si oppone moltiplicato per l'ipotenusa. Nel nostro caso l'altezza
) cioè 60 senx . Se consideriamo anche gli
diventa 6 senx e l'area del parallelogramma 10(6senx
angoli da 180° a 360° otteniamo altezze negative e quindi aree negative. Ruotando in un verso o
nell'altro otteniamo angoli di ampiezza variabile, positivi o negativi secondo la convenzione usata.
Utilizziamo il software Cabri per disegnare il grafico di y senx, quello di y 6senxe di
y 60senx
. Riportiamo la descrizione della costruzione con i comandi di Cabri utilizzati: Mostra
gli assi; prendi un Punto G sull’asse x e trova le Coordinate, calcola con Calcolatrice il seno
dell’ascissa di G. Porta la misura fuori dalla calcolatrice e Trasporta misura sull’asse y. Dal punto
individuato disegna Retta parallela ad x e poi Retta perpendicolare a questa retta e passante per G.
Disegna il Punto di intersezione T. Usa Traccia o Luogo per generare la sinusoide (cliccando prima
sul punto che traccia il luogo T e poi sul punto G che lo genera). Nascondi poi le rette, i punti e le
misure.
6
Notiamo dai grafici di queste funzioni che l’angolo riportato sull’asse x è in radianti; tutte hanno lo
stesso periodo 2π (nel senso che si ripetono identiche dopo un intervallo di angolo di ampiezza 2π),
ma un diverso codominio, rispettivamente [-1,+1], [-6,+6] e [-60,+60].
7
Il moto armonico semplice e la sinusoide con Cabri
Vogliamo provare, attraverso una simulazione con Cabri, che il moto armonico semplice è un moto
periodico e che il grafico che descrive la posizione del punto in funzione del tempo è una semplice
sinusoide di ampiezza costante. Riprendiamo in esame, con la professoressa, alcuni moti già
studiati l'anno scorso: abbiamo un moto armonico semplice ogni qualvolta una particella, oscillante
avanti e indietro rispetto ad una posizione di equilibrio, è soggetta ad una forza con intensità
proporzionale allo spostamento, direzione uguale a quella dello spostamento e verso opposto (legge
di Hooke). Il moto armonico è strettamente legato al moto circolare uniforme, in quanto la
proiezione del moto circolare su una qualsiasi retta dà luogo ad un moto armonico. Con Cabri
simuliamo un moto circolare uniforme di un punto materiale P e il moto armonico della proiezione
Q di tale punto sul diametro verticale della circonferenza. In un riferimento cartesiano riportiamo
sull’ascissa l’angolo al centro, oppure l’arco, percorso dal punto materiale che descrive il moto
circolare uniforme a partire da una posizione iniziale di riferimento della circonferenza e,
sull’ordinata, riportiamo la distanza dal centro O della proiezione di P sul diametro verticale.
(Ricordiamo che l’ampiezza dell’angolo al centro e la lunghezza dell’arco di circonferenza
corrispondenti sono grandezze direttamente proporzionali. Se rappresenta l’angolo al centro
misurato in radianti e r il raggio delle circonferenza, allora l’arco misura r ). Al variare
dell’angolo al centro la distanza della proiezione di P da O descrive una sinusoide. Descriviamo la
costruzione: Mostra gli assi, disegna Circonferenza nell’origine, Punto P sulla circonferenza, Retta
perpendicolare all’asse y per P, Punto Q intercettato sull’asse y. L’Animazione muove il punto P di
moto circolare uniforme e questo trascina il punto Q in un moto armonico lungo il diametro
verticale.
Vogliamo riportare su un sistema cartesiano la variazione della distanza di Q (proiezione di P sul
diametro verticale) dal centro O della circonferenza al variare dell’arco AP oppure dell’angolo AOP.
Non siamo riusciti, con una semplice procedura, a misurare gli angoli orientati che differiscono di
multipli di angolo giro (per usare in modo dinamico la variazione dell’arco, o dell’angolo, e
8
calcolare la corrispondente variazione della distanza QO). Ripetiamo allora la costruzione con Cabri
in modo diverso: Circonferenza, Retta orizzontale per il centro della circonferenza, Punto A
intersezione a destra della circonferenza con l'asse; Retta perpendicolare per quest'ultimo punto;
Mostra gli assi di origine A e coincidenti con le rette ortogonali già costruite. Ora, sull'asse
orizzontale del riferimento cartesiano, invece di riportare l'angolo al centro, oppure l'arco percorso
da P a partire dal punto iniziale A, prendiamo un Punto qualunque G e trovate le sue Coordinate,
con il comando Trasporta, riportiamo sulla circonferenza, a partire dal punto A, la misura
dell'ascissa del punto G (Cabri considera positivo il verso antiorario di percorrenza della
circonferenza); viene individuato un punto P, estremo dell'arco di origine A. (In questo modo
l'ascissa di G è lunga come l'arco AP). Spostando il punto G sull'asse delle ascisse, il punto P si
muove di moto circolare. La proiezione di P sul diametro verticale della circonferenza descrive un
moto periodico dall'alto in basso e viceversa (al variare di G con velocità costante, il punto P si
muove di moto circolare uniforme e Q di moto armonico). L'ascissa di G e l'ordinata di Q
individuano un punto T che descrive una sinusoide. Questo risultato viene evidenziato con
Animazione (inserendo una molla al punto G) oppure con Traccia o Luogo (“cliccando” prima su T
e poi su G). La sinusoide generata dal comando Traccia scompare “toccando” la barra del cursore;
Luogo, invece, disegna una sinusoide definitiva. L'osservazione del grafico e dell'unità di misura
dell'asse x evidenziano che la variazione della lunghezza dell'arco di circonferenza, di origine A e
secondo estremo P, determina la variazione dell'ordinata di P e quindi della distanza Q da O, centro
della circonferenza. Se la variabile indipendente fosse l'angolo al centro in radianti, dovremmo fare
una costruzione diversa rispetto alla precedente; il punto che genererà la sinusoide sarà ancora G,
ma il punto T che traccerà la sinusoide avrà per ascissa il rapporto tra l'ascissa del punto G e il
raggio della circonferenza e avrà per ordinata quella del punto Q. Il primo grafico risulterà solo più
“dilatato” rispetto al secondo.
9
La professoressa ci chiede di trovare il grafico che descrive, al variare del tempo, la variazione della
distanza del punto Q dal centro della circonferenza. Mentre il punto P descrive un moto circolare
uniforme, la sua proiezione Q sul diametro verticale descrive un moto armonico. Il punto P percorre
un giro completo di circonferenza (periodo) nello stesso intervallo di tempo in cui Q percorre due
volte il diametro, da una posizione iniziale, avanti e indietro, fino a ritornare nella posizione di
partenza. Se è l'angolo al centro in radianti e è la velocità angolare costante del punto P che
descrive un moto circolare uniforme, allora il tempo t impiegato da P a percorrere l'arco AP è dato
da t / ed è direttamente proporzionale all'ampiezza dell'angolo al centro. Viceversa l'angolo
è dato da t . Se riportiamo sull'asse delle ascisse il tempo (direttamente proporzionale
all'ampiezza dell'angolo al centro) e in quello delle ordinate la distanza di Q dal centro della
circonferenza otteniamo ancora una sinusoide. La legge oraria del moto armonico del punto Q si
può ricavare facilmente ricordando la definizione di seno di un angolo. Indicato con r il raggio
della circonferenza, se all’istante t 0 il raggio vettore per P forma un angolo nullo con l’asse x
t ; se all’istante t 0
positivo, all'istante t 0 la proiezione del punto P sull'asse y vale: y rsen
il raggio vettore per P forma un angolo 0 con l’asse x positivo, all'istante t 0 la proiezione del
(
t). Possiamo ripetere il ragionamento proiettando P sull’asse
punto P sull'asse y vale yrsen
t e se 0 si ha invece xrcos(
t). Quest'ultima è la legge oraria
x, otteniamo x rcos
che si ricava risolvendo le equazioni del moto armonico. Ci poniamo ora un domanda. La “traccia”
10
del pendolo reale da noi costruito è davvero una sinusoide? Abbiamo bisogno di alcuni riferimenti
teorici. Un pendolo semplice è costituito da una piccola sfera vincolata ad un sostegno per mezzo di
un filo flessibile, inestensibile e di massa trascurabile. La posizione d’equilibrio del pendolo è
quella nella quale il centro di sospensione, il filo teso e il centro della sfera sono allineati lungo la
verticale. Se si allontana la sfera dalla posizione di equilibrio e si lascia libera essa inizia ad
oscillare attorno a questa posizione. Il periodo del pendolo è il tempo che esso impiega a compiere
una oscillazione completa, cioè a tornare nella posizione da cui è partito e nelle stesse condizioni di
movimento. La professoressa ci fa vedere che il moto del pendolo semplice è dovuto alla sola
componente della forza peso ortogonale alla direzione del filo (l'altra componente, lungo la
direzione del filo, è equilibrata dalla tensione del filo stesso). La componente ortogonale al filo è
direttamente proporzionale a sen (dove è l'angolo formato dalla verticale e dal filo) ma, per
angoli piccoli, sen è ben approssimato da e allora, ricordando che il peso di un corpo è il
prodotto della sua massa m per l'accelerazione di gravità g , la sfera è soggetta ad una forza
F mg
(il segno – indica che è una forza di richiamo verso la posizione di equilibrio). Questa
equazione è matematicamente identica a F kx e, ricordando che questa è legge di Hooke valida
per ricavare l'equazione oraria del moro armonico semplice, deduciamo che il moto del pendolo, per
piccoli angoli, è armonico e che il grafico della legge oraria è una sinusoide (o una cosinusoide).
m g s in
m g cos
mg
11
Il parallelogramma che “avanza” con Cabri e l'impronta della sinusoide tracciata dall'altezza
Descrizione: Circonferenza di centro O, Semiretta orizzontale verso destra di origine O, Punto A di
intersezione di questa con la circonferenza, Distanza OA, Calcolatrice per trovare un quarto di
circonferenza poi riportata sulla semiretta con Compasso a partire da A verso destra. (Queste due
ultime istruzioni servono a iniziare la simulazione del movimento del futuro parallelogramma a
partire dal rettangolo). Individuiamo un Punto G di una nuova Semiretta di origine B sovrapposta
alla precedente (nascondi la semiretta di origine il centro della circonferenza e il compasso usato
per la costruzione). La Distanza GA, cambiata di segno con Calcolatrice, viene riportata sulla
circonferenza da A con Trasporto di misura; sia P il punto estremo dell'arco. (Cabri considera
negativo il verso orario di percorrenza della circonferenza; per migliorare la simulazione del moto
verso destra abbiamo bisogno di rotazioni orarie). Osserviamo che muovendo il punto G sulla
semiretta, il corrispondente punto P sulla circonferenza si muove di moto circolare. Se G “avanza di
moto rettilineo uniforme, P si muove di moto circolare uniforme orario. Riportiamo a partire da G
un Segmento che sarà la base del nostro parallelogramma articolato. I punti estremi di tale segmento
saranno i centri di due Circonferenze di raggio uguale alla circonferenza di partenza che
simuleranno i dischi di plexiglas. Nel Punto Medio tracciamo il Segmento perpendicolare, di
lunghezza uguale al diametro, che simulerà il listello sul quale potremo misurare l'altezza del
parallelogramma. Riportiamo, per gli estremi dei punti di base, due Segmenti paralleli al raggio
della circonferenza iniziale OP e lunghi quanto i lati obliqui del nostro parallelogramma. Uniamo i
quattro punti estremi di questi segmenti con un Poligono. Muovendo il punto G, il punto il raggio
OP cambia direzione e così pure i lati obliqui del parallelogramma. Troviamo il Punto di
intersezione T dell'asse del segmento di base con il lato opposto, la sua distanza dalla base
rappresenta l'altezza del parallelogramma. Spostando il punto G dalla sua posizione iniziale e quindi
variando l'arco (o l'angolo al centro) descritto da P, il punto T descrive la sinusoide. Tracciamo due
rette parallele al lato di base del parallelogramma passanti per i punti C e D: queste simuleranno le
guide del nostro dispositivo mobile. Nascondiamo le rette e le circonferenze usate per la costruzione
e coloriamo le parti che vogliamo evidenziare
12
13
Il pendolo fisico con Cabri e l'impronta della sinusoide lasciata dal pendolo
Descrizione: Semiretta verticale verso il basso di origine O, centro di sospensione del pendolo.
Circonferenza di centro A, appartenente alla semiretta, e raggio molto più piccolo della distanza
OA. (Questo servirà per approssimare il seno dell'angolo di spostamento con l'angolo stesso). Retta
perpendicolare per A alla semiretta di partenza e Punto B intersezione a destra della retta con la
circonferenza; Retta perpendicolare per B alla retta precedente; al di sotto del punto B prendere un
Punto C qualunque. Circonferenza di centro O e raggio OC; Punto di intersezione D con la verticale
di origine O; Simmetria assiale di C rispetto alla verticale per O: si individua un punto E; Arco di
circonferenza CDE; Punto G sulla circonferenza e Retta parallela per G alla semiretta verticale di
origine O. Si individua un Punto P di intersezione della retta con l'arco CDE che rappresenta il
centro della sfera del nostro pendolo; il segmento PO rappresenta il filo inestensibile e privo di
massa del pendolo. Coloriamo per evidenziare le parti importanti e nascondiamo le rette e i punti
che non riteniamo importanti.
Animazione (molla applicata a G) mette in movimento il punto G in moto circolare uniforme. La
proiezione del moto del punto G sulla corda dell'arco CE è, come sappiamo, un moto armonico. Per
piccoli angoli la corda si “confonde” con l'arco sotteso e il moto del punto P lungo l'arco CE (moto
del pendolo) diventa armonico come nella corda CE. E' possibile evidenziare le forze in gioco che
agiscono sul pendolo semplice e osservare come esse variano dinamicamente al variare dell'angolo
formato dalla verticale di origine O e dal filo OP.
O
Pendolo semplice
La sferetta di centro
P è attaccata ad un
filo inestensibile di
massa trascurabile e
sospeso nel punto
O. Mentre G si
muove di moto
circolare uniforme il
pendolo semplice
descrive l'arco CE
G
B
A
E
P
C
14
E' possibile anche simulare un pendolo che “traccia” la sinusoide.
O
O
P
G
B
G
T
Nella figura a sinistra è raffigurato un pendolo semplice e la componente della forza peso della sfera
ortogonale al filo che determina il moto. Nella figura a destra il punto G che genera il luogo,
muovendosi di moto rettilineo uniforme, trascina il punto P di moto circolare uniforme. Questo
15
moto, proiettato sulla corda e quindi sull'arco del pendolo, genera un moto armonico. Il punto T che
traccia il luogo è determinato dall'intersezione della retta per il punto G e perpendicolare alla
direzione del suo moto e dalla proiezione di P sul diametro parallelo alla corda che sottende l'arco in
cui si muove il pendolo.
Dobbiamo rilevare, a conclusione del lavoro, la possibilità di aver commesso alcuni errori dovuti
all'eccessiva semplificazione dei modelli di descrizione della realtà. Pensiamo al moto del pendolo
reale considerato armonico semplice e alla sua “traccia”; pensiamo ai moti descritti applicando il
comando Animazione di Cabri e considerati, erroneamente, rettilinei uniformi o circolari uniformi.
Il comando Traccia o Luogo, facendoci però vedere la sinusoide, ci ha rassicurato della bontà degli
algoritmi utilizzati per descrivere i fenomeni. La metodologia applicata in campi diversi della
conoscenza, seguendo le linee guida dell'insegnante, ci sarà utile anche in futuro. Oggi abbiamo le
idee meno confuse nei riguardi della funzione sinusoidale e del suo grafico; ci auguriamo di
rincontrarla nei nostri studi in campi molto diversi, in problemi di topografia e nello studio di
fenomeni periodici di varia natura, e di riconoscerla facilmente come una “vecchia amica”.
STUDENTE: GIACOMO CAPACCIONI
STUDENTE: ALESSANDRO FAVARONI
STUDENTE: FRANCESCO GEMIGNANI
STUDENTE: FEDERICO PELAGAGGE
INSEGNANTE: CLAUDETTE PENTUCCI
16












