MISURE MECCANICHE E TERMICHE
A.A. 2012-13
Lezione n.26 (19.11.2012)
ESTENSIMETRIA
STATI DI DEFORMAZIONE PIANI
Nel caso di forza normale, momento flettente, momento torcente, le direzioni principali sono note.
Se ciò non accade, per conoscere lo stato di sollecitazione nell’intorno di un punto occorre conoscere
l’angolo che le direzioni principali formano con una coppia di assi di riferimento x^y , e l’entità delle
sollecitazioni principali 1 e 2. Allo scopo si utilizzano le “rosette estensimetriche”, formate da tre
griglie su una stessa base; le griglie possono formare angoli di 90°, 135° e 135° (direzioni x, y, –
come in figura), oppure 120°,120° e 120° (direzioni 30°, 90°, 150° - come in figura) . Nel sistema di tre
equazioni e tre incognite (, 1 e 2), le deformazioni delle tre griglie costituiscono i termini noti.
Si osservi che, mentre nel caso di forza normale, momento flettente, momento torcente, si utilizza
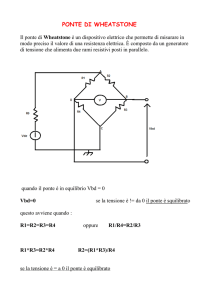
sempre, anche con più di un estensimetro, un solo ponte di Wheatstone, nel caso di rosetta
estensimetrica ogni griglia fa capo a un ponte di Wheatstone , e quindi si utilizzano tre ponti.
Scendendo più in dettaglio, considerando il caso di griglie a 90°, 135°, 135°, si supponga che la
direzione 1 (in corrispondenza alla quale si ha la sollecitazione principale 1), formi angolo con
l’asse x, e quindi che la direzione 2 (in corrispondenza alla quale si ha la sollecitazione principale 2),
formi angolo con l’asse y.
Pertanto l’angolo 1^y è pari ad /2, quello con la bisettrice degli assi ad /4.
y ( +/2)
2 (2)
/4 (/4)
x ()
1 (1)
1
1
x
cos
sin
2
Si consideri un prisma triangolare di altezza unitaria; la sollecitazione x sia applicata alla faccia
di larghezza unitaria; le sollecitazioni 1 ed 2 alle facce di larghezza cos e sin .
Si dimostra facilmente che:
x 1 cos 2 2 sin 2
segue che:
y / 2
1 2
e che:
/ 4 / 4
2
1 2
2
1 2
2
2
1 2
2
cos 2 ;
cos 2
1 2
2
1 2
sin 2 .
Per quanto riguarda le deformazioni rilevate dalle tre griglie, risulta:
1
2 1 2
1 1 2 1 2
( x y )
cos 2 - ( 1
cos 2 )] =
[
E
2
2
2
2
E
2
2
1
= (1 ) 1
(1 ) 1
cos 2
E
2
2
x
2 1 2
1
1 2 1 2
( y x ) [ 1
cos 2 - ( 1
cos 2 )]=
E
E
2
2
2
2
2
2
1
= (1 ) 1
(1 ) 1
cos 2
E
2
2
2 1 2
1
1 2 1 2
/ 4 ( / 4 3 / 4 ) [ 1
sin 2 - ( 1
sin 2 )] =
E
E
2
2
2
2
2
2
1
= (1 ) 1
(1 ) 1
sin 2 ,
E
2
2
y
ove E e sono il modulo di Young e il coefficiente di Poisson del materiale cui è applicata la rosetta
estensi metrica.
Risolvendo pertanto il sistema di tre equazioni in tre incognite, si trova:
tg 2
2 / 4 x y
x y
x y
1
1
1
2( x y ) 2 2( / 4 y ) 2
x y
1
2 E / 2
2( x y ) 2 2( / 4 y ) 2 .
1
1
1 E / 2
CENTRALINE ESTENSIMETRICHE
Sono gli elaboratori utilizzati per rilevare le uscite degli estensimetri; svolgono i seguenti compiti:
a)- Completare il ponte di Wheatstone
b)- Alimentare il ponte
c)- Bilanciare il ponte
d)- Amplificare lo squilibrio del ponte
e)- Calibrare la catena di misura.
Completare il ponte significa aggiungere ai “rami attivi”, cioè ai rami del ponte costituiti da
estensimetri, le resistenze necessarie a formare un ponte di quattro rami.
Se, per esempio i rami attivi sono 2 (1 e 2), il ponte viene completato da due resistenze R3 ed R4, il cui
valore è generalmente pari a 120 Ω o a 350 Ω (più raramente 600 Ω).
Alimentare il ponte significa fornirgli la tensione E (ordine di qualche volt) necessaria al suo
funzionamento. Più elevata è la tensione di alimentazione, più elevato è lo squilibrio rilevato, ma più
elevato è l’effetto Joule dovuto al passaggio di corrente; con tensioni dell’ordine visto, l’intensità di
corrente è dell’ordine dei 10 mA.
Rcal
R1
Rbil
R4
e
E
R3
R2
A
S.T.
Rcal
Bilanciare il ponte, significa operare sulla resistenza di bilanciamento (Rbil, resistenza di elevato valore,
dell’ordine delle centinaia di k , e disposta in parallelo al ponte), in modo che sia verificata la R1 R3 =
R2 R4 , ovvero che quando il pezzo di cui si vuol rilevare la deformazione è nella configurazione di
riferimento, la tensione di squilibrio e sia nulla: allo scopo il cursore che collega il nodo R3-R4 a Rbil,
si sposta su Rbil finché non è verificata la condizione di equilibrio
Amplificare lo squilibrio significa agire sull’amplificatore A in modo che la tensione uscente
dall’amplificatore stesso abbia un livello tale (Ge, ove G è il guadagno), da poter essere rilevata dallo
strumento terminale S.T.
Calibrare la catena di misura significa risalire dalla tensione rilevata dallo strumento terminale alla
deformazione (sensibilità della catena di misura).
a)- Si consideri la e = ¼ EAGF, ove e è lo squilibrio rilevato dallo strumento terminale, F il fattore
di taratura degli estensimetri, A il fattore di ponte, la deformazione da rilevare. Calcolato A, se E, G,
F, sono noti con elevata precisione, è immediato risalire da e, a . Posto per es., E = 2V, G = 1000,
F = 2, considerando A=1, a 1m/m di deformazione, corrisponde 1 mV di squilibrio.
b)- Se quanto sopra non si verifica, si può mettere in parallelo (a ponte bilanciato), a una delle
resistenze un elevata resistenza Rcal (resistenza di calibrazione, dell’ordine del centinaio di k ). Si
ponga, per es., Rcal in parallelo a R4. In tal caso, a conti fatti si ha uno squilibrio:
e/E = ¼ R4/( R4+ Rcal);
si può considerare tale squilibrio provocato da una deformazione fittizia detta deformazione di
calibrazione cal; risulta allora:
cal = ¼ R4/[F( R4+ Rcal)];
con un opportuno guadagno dell’amplificatore si può ottenere una sensibilità della catena che consenta
di determinare rapidamente le deformazioni (per es., 1mV/m/m).
Se è applicato più di un estensimetro, occorre tener conto del fattore di ponte A.