File

Probl. 121 pag. 198
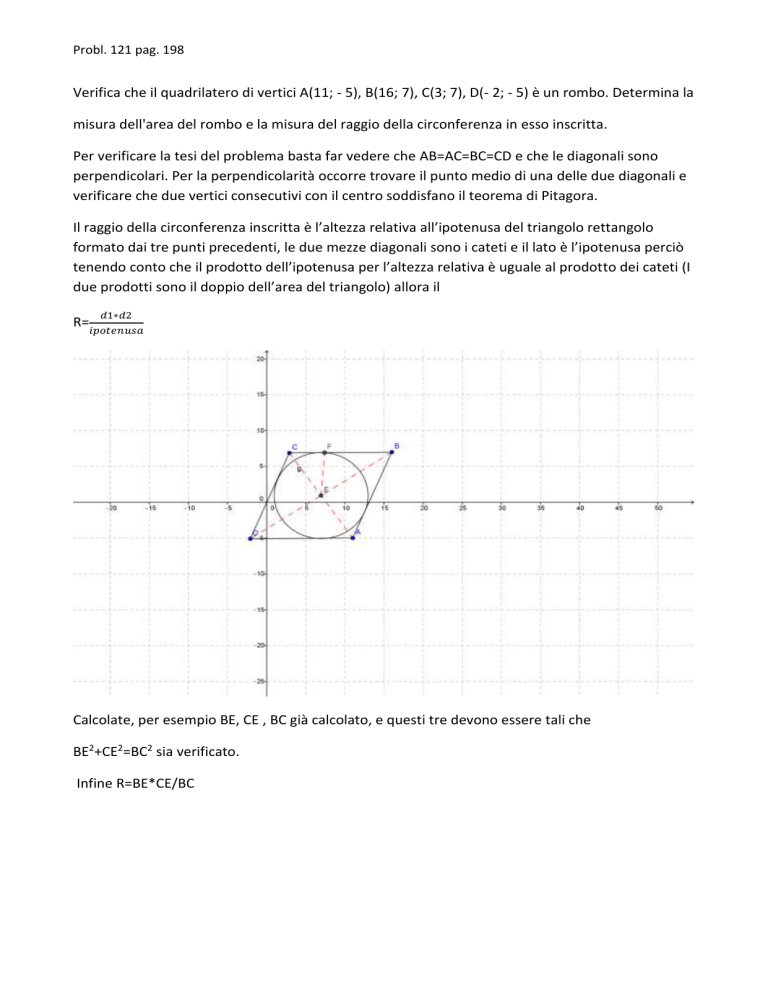
Verifica che il quadrilatero di vertici A(11; - 5), B(16; 7), C(3; 7), D(- 2; - 5) è un rombo. Determina la
misura dell'area del rombo e la misura del raggio della circonferenza in esso inscritta.
Per verificare la tesi del problema basta far vedere che AB=AC=BC=CD e che le diagonali sono
perpendicolari. Per la perpendicolarità occorre trovare il punto medio di una delle due diagonali e
verificare che due vertici consecutivi con il centro soddisfano il teorema di Pitagora.
Il raggio della circonferenza inscritta è l’altezza relativa all’ipotenusa del triangolo rettangolo
formato dai tre punti precedenti, le due mezze diagonali sono i cateti e il lato è l’ipotenusa perciò
tenendo conto che il prodotto dell’ipotenusa per l’altezza relativa è uguale al prodotto dei cateti (I
due prodotti sono il doppio dell’area del triangolo) allora il
𝑑1∗𝑑2
R=𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎
Calcolate, per esempio BE, CE , BC già calcolato, e questi tre devono essere tali che
BE2+CE2=BC2 sia verificato.
Infine R=BE*CE/BC