Lezione 4
La domanda di lavoro.
1. Il modello-base. Abbiamo suggerito più sopra che dal punto di
vista delle imprese il lavoro è "solo" un fattore di produzione, e
quindi la teoria della domanda di lavoro è sostanzialmente un caso
particolare della domanda dei fattori di produzione, che avete già
studiato nel corso di economia. Cominceremo accettando l'ipotesi
di concorrenza perfetta, il che vuol dire
(a) che il prezzo del lavoro, il salario, è dato per l'impresa;
(b) che a quel prezzo l'impresa trova tutta l'offerta di lavoro
che vuole;
(c) che il prezzo di vendita del prodotto dell'impresa è dato;
(d) che a quel prezzo l'impresa può vendere la quantità che vuole.
Più avanti complicheremo il modello e passeremo dalla domanda
dell'impresa individuale alla domanda aggregata. Il punto di
partenza del discorso è che poiché il lavoro è un fattore di
produzione, la sua domanda dipende dall'equilibrio del produttore
sul mercato dei beni. Ricorderete che da questo punto di vista è
importante distinguere fra breve periodo e lungo periodo; nel
primo lo stock di capitale è dato. Cominciamo dal breve periodo.
2. La domanda di lavoro nel breve periodo. La domanda di lavoro è
una domanda derivata o indiretta, nel senso che essa dipende dalla
domanda di prodotti finali per l'impresa; per non appesantire il
discorso saltiamo la discussione di come la domanda di lavoro
viene dedotta dalla teoria dell'equilibrio del produttore.
Partiamo invece più
a valle, e cioè dalla figura 1; ricordiamo
che in essa assumiamo che lo stock di capitale sia dato1.
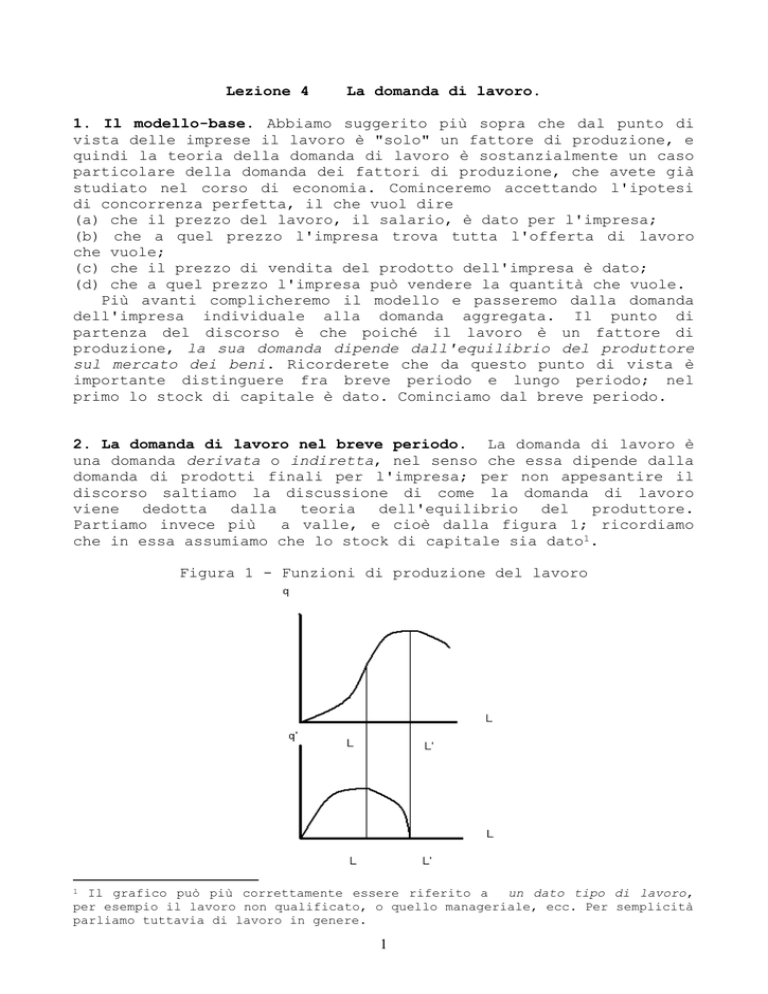
Figura 1 - Funzioni di produzione del lavoro
Il grafico può più correttamente essere riferito a
un dato tipo di lavoro,
per esempio il lavoro non qualificato, o quello manageriale, ecc. Per semplicità
parliamo tuttavia di lavoro in genere.
1
1
Il grafico superiore individua la quantità di produzione in
funzione della quantità di lavoro. Inizialmente, all'aumentare
della quantità di lavoro la produzione cresce sempre di più (per
esempio perché se c'è un solo lavoratore, parte degli impianti
saranno inutilizzati, e all'arrivo del secondo la produzione più
che raddoppia), quindi sempre di meno; alla fine i lavoratori
saranno talmente tanti che cominceranno a "pestarsi i piedi", e
l'effetto sulla produzione sarà addirittura negativo. Ciò si
riflette nell'andamento della produttività marginale del lavoro,
nel grafico inferiore. Naturalmente, il primo tratto ha scarsa
rilevanza (si veda l'esercizio 1); escludendo questo tratto,
possiamo allora dire che la produttività marginale del lavoro, q',
è calante. Questa produttività marginale spesso viene indicata con
mpp (marginal physical product). Moltiplichiamo ora i valori di q'
(ovvero mpp) nella parte (b) per il prezzo del prodotto, p, in
modo da ottenere la funzione della produttività marginale in
termini monetari, r, cioè una funzione del ricavo marginale del
lavoro.
3. seguito. Poiché p è fisso (siamo in concorrenza perfetta!) il
grafico avrà lo stesso andamento. Lo vediamo nella figura 2.
Figura 2 - Derivazione della domanda di lavoro dell'impresa nel
breve periodo.
Nella figura 2, la curva individua appunto il ricavo marginale
del lavoro, mentre i segmenti tratteggiati individuano diversi
valori del costo marginale del lavoro, che altro non è che il
salario unitario, w. Sappiamo che se il ricavo marginale supera il
costo marginale conviene estendere l'impiego del fattore, e in
caso contrario ridurla; quindi l'intersezione fra
il segmento
corrispondente a un valore di w e la curva di r individua la
quantità di L domandata per quel valore di w. Come si vede, e come
ovvio, ceteris paribus la domanda di lavoro cala al crescere di w.
2
In
pratica, l'impresa domanda quella quantità di lavoro tale
per cui il ricavo marginale del lavoro è eguale a w. L'impresa
vorrà cioè quella quantità di lavoro per cui
w = mpp*p
dove w è il salario, p è il prezzo (dato) del prodotto e mpp è la
produttività marginale in termini fisici del lavoro. Al crescere
di w, poiché p è dato la condizione si realizza se cresce mpp; e
poiché mpp cresce se cala L, abbiamo che via via che cresce w la
condizione è rispettata se cala L.
In termini ancora più semplici: se cala w cala il costo
marginale del prodotto, e quindi converrà espandere la produzione,
e quindi assumere nuovo L.
4. Mercato dei beni non concorrenziale.
Supponiamo ora che
l'impresa operi ancora in un mercato del lavoro concorrenziale, ma
in un mercato dei beni monopolistico. Ricorderete che nel caso
della concorrenza perfetta l'impresa può vendere la quantità che
vuole (la funzione di domanda è orizzontale), mentre nel caso del
monopolio la funzione di domanda è inclinata negativamente.
Supponiamo per semplicità una relazione lineare, p = a - bQ. Il
ricavo totale è pQ = aQ - bQ2, il ricavo medio a-bQ (cioè, come
ovvio il prezzo), e il ricavo marginale è a-2bQ. Il ricavo
marginale
è
quindi,
come
sappiamo,
inferiore
al
prezzo;
chiamiamolo r'.
Ora,
la condizione di equilibrio che determina la domanda di
lavoro è che il costo marginale del lavoro sia eguale al ricavo
marginale ad esso imputabile. Nel caso della concorrenza perfetta
è quella che abbiamo visto: w=mpp*p. Nel caso del monopolio essa
sarà
w = mpp*r'. Poiché r'<p, ceteris paribus la condizione si
realizzerà a parità di w per un valore di mpp maggiore, e quindi
per un valore di L minore.
In altri termini: il monopolio domanda meno lavoro di un'impresa
concorrenziale. Anche qui è utile fornire la spiegazione "di buon
senso" di ciò: il monopolio, sappiamo, produce meno di un'impresa
concorrenziale, e vende a prezzi maggiori. Ma se produce meno,
avrà anche bisogno di meno lavoro. Poiché questo risultato è
dovuto all'inclinazione negativa della curva di domanda di beni
fronteggiata dall'impresa, esso si avrà anche nel caso di
oligopolio e in quello di concorrenza monopolistica.
5. La domanda di lavoro dell'impresa nel lungo periodo. Nel lungo
periodo, l'impresa può modificare la sua dotazione di capitale.
Supponiamo allora che l'impresa sia in equilibrio, e che produca
una data quantità impiegando quella quantità di capitale per cui
la produttività marginale del capitale è eguale al suo prezzo e la
produttività marginale del lavoro è eguale a w. Supponiamo ora che
w cali. In tal caso, aumenterà L, e poiché una maggiore quantità
di lavoro viene applicata allo stesso capitale, aumenterà la
3
produttività marginale del capitale. Questo non aveva conseguenze
nel breve periodo, perché l'impresa non poteva modificare lo stock
di capitale; qui però si, e l'impresa aumenterà quindi lo stock di
capitale. Ciò farà aumentare la produttività marginale del lavoro,
e quindi aumenterà ancora L, e così via. Come risultato, e come
dovrebbe essere intuitivo, l'effetto di una variazione di w nel
lungo periodo è più ampio di quello di breve periodo; ovvero, la
funzione di domanda di lungo periodo è più piatta, ovvero ancora
più elastica di quella di breve periodo. Graficamente, questo
processo è illustrato dalla figura 3.
Figura 3 - domanda di lavoro dell'impresa nel breve e nel lungo
periodo
Inizialmente, il salario è w', e l'impresa acquista quella
quantità di lavoro per cui la produttività marginale del lavoro in
termini monetari, mpp*p è pari a w, cioè L'. Ora w diminuisce fino
a w”, e quindi l'impresa occuperà unita di lavoro con una
produttività minore, e quindi espanderà L fino a L". Ma l'aumento
di lavoro aumenta la produttività marginale del capitale, e quindi
l'impresa acquisterà nuovo capitale. Ciò aumenterà la produttività
marginale del lavoro, e quindi in L" questa produttività sarà più
alta che w. L'impresa allora aumenterà ancora L, fino a giungere,
alla fine del processo, a L"'.
Si noti che abbiamo implicitamente supposto che non vi siano
vincoli dal lato della domanda; il che è perfettamente sensato a
livello di impresa concorrenziale, ma non a livello aggregato.
Questo ci porta all'argomento successivo.
6. La domanda di lavoro aggregata. La domanda di lavoro aggregata
non è la semplice somma delle domande individuali: infatti, a
livello di settore produttivo (ovvero di industria, come si usa
anche dire) non si può supporre che la domanda venga esercitata da
un
soggetto
interamente
price-taker.
Se
w
-per
esempiodiminuisce, tutte le imprese aumenteranno l'occupazione, la
produzione aumenterà e il prezzo del bene diminuirà; questo
effetto di ritorno non si aveva a livello di singola impresa, dove
il prezzo non reagiva a una variazione della produzione.
4
Possiamo
intuire
cosa
succederà.
Supponiamo
appunto
una
diminuzione di w. Le imprese aumenteranno la produzione e
l'occupazione. Allora il prezzo del bene scenderà, e quindi anche
la produttività marginale del lavoro (che, ricordiamo, è mpp*p).
Le imprese si troveranno in una situazione in cui pagano un
salario più alto della produttività marginale del lavoro. Come
risultato, dovranno ridurre L. Quindi alla fine l'aumento
complessivo di L è minore di quello che avremmo sommando l'aumento
di ciascuna impresa concorrenziale. La domanda di lavoro aggregata
è quindi meno elastica, ovvero più ripida, di quella individuale,
come illustrato nella figura 4.
Figura 4 - domanda di lavoro aggregata e individuale
Inizialmente un'impresa tipica (una di un insieme di imprese tutte
eguali) è in equilibrio in x, con w=w'=r' e L=L'. w diminuisce, e
l'impresa si sposta in y, con w=w" e L=L". Ma poiché tutte le
imprese fanno così, p diminuisce, e quindi anche r'=mpp*p. La
funzione di r' si separa da quella di w, e diventa la linea rossa.
Come si vede, in corrispondenza di L"
w (=w") è maggiore di
r'(=r"); l'impresa dovrà dunque spostarsi in z, con L=L"' e w=r'.
Sommando i valori di L per le n imprese, abbiamo come domanda
aggregata di L inizialmente nL', e alla fine non nL" ma nL"'.
Abbiamo già osservato come questo risultato fa sì che non sia
possibile generalizzare all'intera economia gli effetti espansivi
di una riduzione del costo del lavoro che un imprenditore prevede
per la sua impresa.
7. Il costo quasi-fisso del lavoro. Fin qui abbiamo supposto che
il costo del lavoro sia solo w, e quindi che esso sia
assolutamente variabile. Nella realtà ci sono dei costi fissi del
lavoro, che fanno sì che (secondo la definizione di Oi, Labour as
a quasi-fixed factor, Journal of Political Economy, 1962) il
lavoro sia un fattore "quasi fisso".
Una parte del costo del lavoro varia infatti con la quantità di
lavoro, ma una parte no. Fra questi ci sono:
a) I costi di turnover.
Assumere e licenziare un lavoratore ha
dei costi amministrativi e umani, che non dipendono da quanto il
lavoratore lavorerà o avrà lavorato;
b) La gestione della posizione del lavoratore entro l'impresa
(tenuta della busta paga, gestione degli accantonamenti, ecc.)
5
c) I contributi che dipendono dal numero di lavoratori e non dalla
quantità di ore lavorate;
d) La parte di retribuzione propriamente fissa, che non dipende
dal "timbrare il cartellino", se c'è; si tratta una voce
particolarmente rilevante per i quadri elevati, spesso sotto la
veste di c.d. fringe benefits, ma rientrano in questa categoria
anche le ferie pagate, nella misura in cui non dipendono dalle ore
effettivamente lavorate;
e) I costi di addestramento;
f) I costi opportunità connessi alle assenze per malattie.
Come si vede, si tratta di un insieme piuttosto fluttuante, e
di difficile quantificazione, ma piuttosto rilevante. Alcuni studi
hanno cercato di misurarne l'incidenza; il più noto, anche se
piuttosto vecchio, è quello di Hart e altri (1988), relativo ai
paesi sviluppati più importanti. L'incidenza era minima in Italia
(15%) e massima nel Regno Unito (26%). Dal punto di vista
analitico, la condizione che individua la domanda di lavoro
r' (=mpp*p) =w
diventa, nel caso più semplice,
r' (=mpp*p) = w+Z
dove Z è il costo fisso connesso a un'unità di lavoro; e quindi la
produttività marginale del lavoro deve essere maggiore di w.
8. Costi fissi e domanda di lavoro. Quale è l'effetto
presenza di costi fissi di lavoro sulla sua domanda?
della
a) Il principale è quello di rendere l'andamento dell'occupazione
meno sensibile all'andamento ciclico della produzione (figura 5).
Infatti, l'imprenditore sarà riluttante a licenziare lavoratori
nella fase calante del ciclo perché ciò ha dei costi, e sarà
riluttante ad assumerli nella fase crescente, per lo stesso
motivo. Inoltre, all'inizio della fase ascendente del ciclo
l'imprenditore tenderà a non assumere subito lavoro aggiuntivo, e
si
avrà
quindi
una
tendenza
all'espansione
del
lavoro
straordinario.
Figura 5 - Ciclo della produzione e ciclo dell'occupazione
6
b) La maggiore stabilità occupazionale del lavoro qualificato. Man
mano
che
si
approfondisce
la
fase
calante
l'imprenditore
licenzierà lavoratori in funzione inversa dei costi cui andrà
incontro se e quando dovrà riassumerli: questa è la spiegazione
della maggiore insicurezza del lavoro non qualificato rispetto a
quello qualificato.
c) L'importanza dell'anzianità. I costi di sostituzione sono
presenti anche se è il lavoratore a licenziarsi. Quindi converrà
all'imprenditore cercare di garantirsi contro l'abbandono dei
lavoratori, soprattutto di quelli più qualificati e quindi
costosi. Un criterio largamente adottato è quello di legare parte
dei guadagni del lavoratore all'anzianità di servizio.
d) la rilevanza del lavoro straordinario: il ricorso al lavoro
straordinario sarà tanto più elevato quanto più alta è la
componente fissa del costo del lavoro.
9. Seguito. Un'ultima considerazione. Poiché, come abbiamo visto,
la produttività marginale del lavoro cresce al calare di L, la
condizione di equilibrio in presenza di costi fissi implica che
l'occupazione sarà minore di quella che si avrebbe se non ci
fossero costi fissi. Tuttavia, ciò non può portare automaticamente
a concludere che sia giusto abolire i costi fissi del lavoro:
infatti, la loro trasformazione da costi fissi a costi variabili
costituirebbe comunque un aumento di w. Si tratta di una
problematica molto interessante dal punto di vista teorico e con
notevole importanza pratica. Per esempio, gran parte del costo di
licenziamento è dovuto al fatto che il lavoratore deve essere
tutelato per i periodi di transizione fra un lavoro e l'altro. Se
la retribuzione cessasse del tutto al momento del licenziamento,
invece di continuare con la cosiddetta "liquidazione" o con
istituti analoghi, il salario dovrebbe essere sufficientemente
elevato da consentire al lavoratore un'autoassicurazione; si è
dimostrato che ciò sarebbe più costoso per l'impresa, a parità di
garanzie, a causa della maggiore avversione al rischio del
lavoratore rispetto all'impresa. Il discorso tuttavia è troppo
complesso perché possiamo affrontarlo qui in modo esauriente.
10. Salario e produttività del lavoro. Fin qui abbiamo supposto
che r' (la produttività marginale del lavoro) e w (il costo
unitario del lavoro) siano indipendenti. Sia la teoria che
l'evidenza empirica suggeriscono che non è così; l'analisi che ne
consegue è nota come teoria del salario-efficienza. In pratica, si
ammette (e si verifica) che normalmente al variare di w la
produttività marginale varia nella stessa direzione. Il motivo di
ciò è triplice.
7
Da una parte, migliori salari corrispondono a una maggiore
soddisfazione che si ricava dal lavoro, e quindi a una
disponibilità a lavorare di più e meglio. Nel caso più brutale di
un'economia molto povera, un salario più alto vuol dire potere
disporre di più calorie; nelle economie più sviluppate il
meccanismo è più sottile, ma comunque intuibile (e bene espresso,
nel caso contrario di una paga troppo bassa, dal brutale slogan
sindacale degli anni 50 "a salario di merda, lavoro di merda")2.
Dall'altra, l'aumento del costo del lavoro obbliga il management a
migliorare l'efficienza in altri settori. Questo è particolarmente
vero nel caso di aumenti improvvisi, come può succedere nel caso
di un rinnovo contrattuale. Infine, salari più alti attireranno i
lavoratori migliori, con effetti positivi sulla produttività.
L'effetto di tutto ciò è che la funzione di domanda di lavoro, sia
aggregata che individuale, è in genere meno elastica di quanto
potrebbe essere suggerito dalla trattazione precedente. In
effetti, è stata proprio la verifica di questa bassa elasticità
che ha indotto all'elaborazione delle teorie discusse negli ultimi
paragrafi.
La
teoria
del
salario-efficienza
ha
altre
implicazioni
rilevanti, in particolare per quanto riguarda la teoria della
disoccupazione. Di essa ci occuperemo quindi ancora più avanti, in
particolare nella lezione 6.
Recenti studi sperimentali hanno inoltre dimostrato che
considerazioni di
fairness hanno una notevole rilevanza nei contratti di lavoro. Il lavoratore che
si considera "trattato bene" lavorerà sovente più e meglio, ceteris paribus, di
uno che non si consideri tale, e ciò può tradursi in un vantaggio per
l'imprenditore. Di ciò ci occuperemo nella lezione 6.
2
8
Esercizi
1. Perché la domanda di lavoro di equilibrio non
ascendente della produttività marginale del lavoro?
può
trovarsi
nel
tratto
2. Sia la produttività marginale del lavoro in termini fisici data da mpp = 20L. w è pari a 10, e il prezzo del bene venduto dall'impresa, p, è pari a 2.
Quanto vale la domanda di lavoro?
3. Sia la funzione di produzione Q = q(L) Q = 100 + 10L - 5L2.
= 12 e p = 3. Quanto L domanda l'impresa?
4. Dato l'esercizio precedente, calcolate di quanto varia
se w cresce del 10%.
Siano inoltre w
la domanda di lavoro
5. Supponiamo un'impresa monopolistica che operi con gli stessi dati
dell'esercizio 3, vale a dire con w=12 e Q = 100 + 10L - 5L2; la funzione di
domanda sia p = 4.042 -0.01Q, di modo che per p=3 Q valga 104.2, come
nell'esercizio 38. Si verifichi che l'impresa domanderà una quantità di L
inferiore a 0.6, la quantità domandata nell'esercizio 3.
6. Quale è la differenza fra monopolio, oligopolio e concorrenza monopolistica?
Soluzioni
1. Perché essendo il prezzo del bene e quello del lavoro costanti, ed essendo
l'impresa in grado di vendere la quantità di prodotto che vuole (siamo in
concorrenza perfetta) un aumento della quantità di lavoro porta necessariamente
a maggiori profitti.
2. Dobbiamo porre 2(20-L) = 10, da cui L = 15.
3. La funzione di mpp è mpp = 10 - 10L. L'impresa domanderà quella quantità di L
per cui 3(10 - 10L) = 12, cioè 0.6, e produrrà 104.2; mpp varrà 4.
5. La funzione di mpp è ancora 10-10L, mentre il ricavo marginale è la derivata
del ricavo totale, cioè di 4.042Q-0.01Q2, ed è
quindi pari a 4.042-0.02Q. la
produttività marginale in termini di valore sarà allora data da (10-10L)(4.0420.02Q). Poiché Q è una funzione di secondo grado di L, questa è una funzione di
terzo grado di
L. Per evitare il complicato calcolo della soluzione di
un'equazione di terzo grado, possiamo ragionare come segue. Supponiamo che
l'impresa si trovi nella stessa situazione di un'impresa di concorrenza, con L
= 0.6 e quindi Q = 104.2, come sappiamo dall'esercizio 3. Il ricavo marginale
del lavoro, mpp*r', vale allora 7.832, che è inferiore a 12. L'impresa deve
quindi aumentare il valore di mpp*r'; per fare ciò deve ridurre il valore di L:
così facendo aumenterà mpp, e inoltre si ridurrà Q, e quindi aumenterà r'.
9










