Esonero di Termodinamica ed Energetica

Esame scritto di Termodinamica
A.A. 2003/04 (11.12.2003)
Problema n. 1 (valido anche come recupero del I esonero)
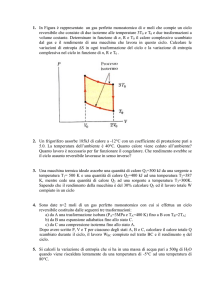
Un contenitore adiabatico è diviso in due parti di ugual volume VA=2.0010-3 m3 da una parete
adiabatica fissa; da entrambe le parti pressione e temperatura hanno gli stessi valori pA=10.1 bar e
TA=273 K. Nella parte di destra c’è idrogeno, in quella di sinistra elio. Tramite un riscaldatore
elettrico viene ceduto all’idrogeno il calore Q=3.00103 J. Successivamente l’elio viene compresso
da un pistone mobile in modo adiabatico reversibile fino a che la sua pressione eguaglia quella
dell’idrogeno e poi il pistone viene bloccato. A seguito di un non perfetto isolamento termico della
parete divisoria, dopo un certo tempo, i due gas raggiungono l’equilibrio termico.
a) Calcolare i valori di p,V e T per l’idrogeno dopo il riscaldamento.
b) Calcolare i valori di p, V e T per l’elio dopo la compressione adiabatica.
c) Calcolare la temperatura finale e la variazione complessiva di energia interna del sistema.
He
H2
Problema n. 2 (valido anche come recupero del II esonero)
2.00 moli di gas perfetto monoatomico compiono una prima trasformazione isoterma reversibile a
temperatura T=287 K da uno stato iniziale A ad uno stato finale B in cui il volume è quattro volte
quello iniziale. Il gas viene quindi posto a contatto termico con una sorgente a temperatura T C<TB e
raggiunge uno stato di equilibrio alla pressione pC=pB. Infine una trasformazione adiabatica
reversibile riporta il gas allo stato A.
a) Sapendo che nel ciclo l’entropia dell’universo è variata di Su = 9.00 J K-1, calcolare, per
ogni trasformazione, la variazione di entropia del gas e la variazione di entropia
dell’ambiente esterno.
b) Calcolare il rendimento del ciclo.
(Testo della soluzione da rivedere nella forma)
Soluzioni
Problema n. 1
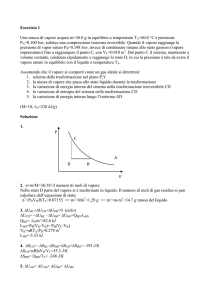
p
C’
C
B
B’
He
Tf
2
H2
A
V
p AV A
 0.890 moli
RT A
L’idrogeno assorbe, in una trasformazione isocora, il calore Q  ncV ( H 2 )(TB  TA )
Q
 435 K.
Quindi, facendo riferimento alla figura, si ha: TB  T A 
ncV ( H 2 )
nRT B
Per le altre variabili si ha: VB  V A  2.00  10 3 m3
pB 
 16.1 bar
VB
b) Per l’elio si ha una trasformazione adiabatica.
a) Per prima cosa si calcola il numero di moli dei due gas: n( He)  n( H 2 ) 
1
p  
La pressione è: pC  p B  16.1 bar. Il volume è dato da: VC  V A  A   1.51  10 3 m3
 pC 
p V  pCVC
 617 J;
Per la temperatura si ha: L AC  U AC  ncV (TC  T A )  A A
 1
L
 329 K.
quindi TC  T A 
ncV ( He )
c) La trasformazione, considerando il sistema “elio + idrogeno” avviene a Q=L=0 quindi:
5 T 3 T
B
2 C  395 K.
ncV ( H 2 )(T f  TB )  ncV ( He )(T f  TC )  0 quindi T f  2
4
U  ncV ( H 2 )(T f  TA )  ncV ( He)(T f  TA )  4nR(T f  TA )  3.61103 J.
Problema n. 2
B
a) Nella trasformazione reversibile AB sappiamo che ΔS TAB
 ΔS gas
AB , essendo un’isoterma
TB
gas
amb
gas
reversibile ΔS AB  n R ln VB /VA  , segue S  ΔS AB  ΔS AB  n R ln VB /VA  =23,1 J/ K.
Per la trasformazione BC si deve considerare il dato sull’entropia dell’universo:
B
Su  ΔSciclo  ΔSTABB  ΔSTBCC  0  n R ln VB /VA   ΔSTBCC , quindi ΔS TBCC  S u  ΔS TAB
 32.1 J/K
gas
ΔS gas
BC  ΔS ciclo  ΔS AB  0  n R ln VB /VA   23.1 J/K.
amb
Per la trasformazione CA, essendo una adiabatica reversibile, ΔSgas
CA  ΔSCA  0
b) Per il calcolo del rendimento è necessario conoscere il calore assorbito e ceduto nel ciclo.
Nella trasformazione adiabatica CA non c’è scambio di calore.
TC
TC
Il calore ceduto dal gas nella trasformazione irreversibile è: Q gas
BC   Q BC  TC S BC .
Si deve calcolare TC: essendo pC=pB= pA/4 si può usare l’espressione dell’adiabatica reversibile:
p
TC  TA  A
 pC
1



1
 0.574  287 K = 165 K
3
Quindi Q gas
BC  5.30  10 J.
gas
Infine Q gas
AB  L AB  nRT A ln
VB
 6.63  10 3 J.
VA
Il rendimento è dato da:
η  1
Q ced
Q gas
BC
 1  gas
 0.201
Q ass
Q AB