Esercizio 1
Una massa di vapore acqueo m=36.0 g in equilibrio a temperatura TA=60.0 °C e pressione
PA=0.100 bar, subisce una compressione isoterma reversibile. Quando il vapore raggiunge la
pressione di vapor saturo PB=0.198 bar, invece di condensare rimane allo stato gassoso (vapore
soprassaturo) fino a raggiungere il punto C, con VC=0.010 m3. Dal punto C il sistema, mantenuto a
volume costante, condensa rapidamente e raggiunge lo stato D, in cui la pressione è tale da avere il
vapore saturo in equilibrio con il liquido a temperatura TA.
Assumendo che il vapore si comporti come un gas ideale si determini:
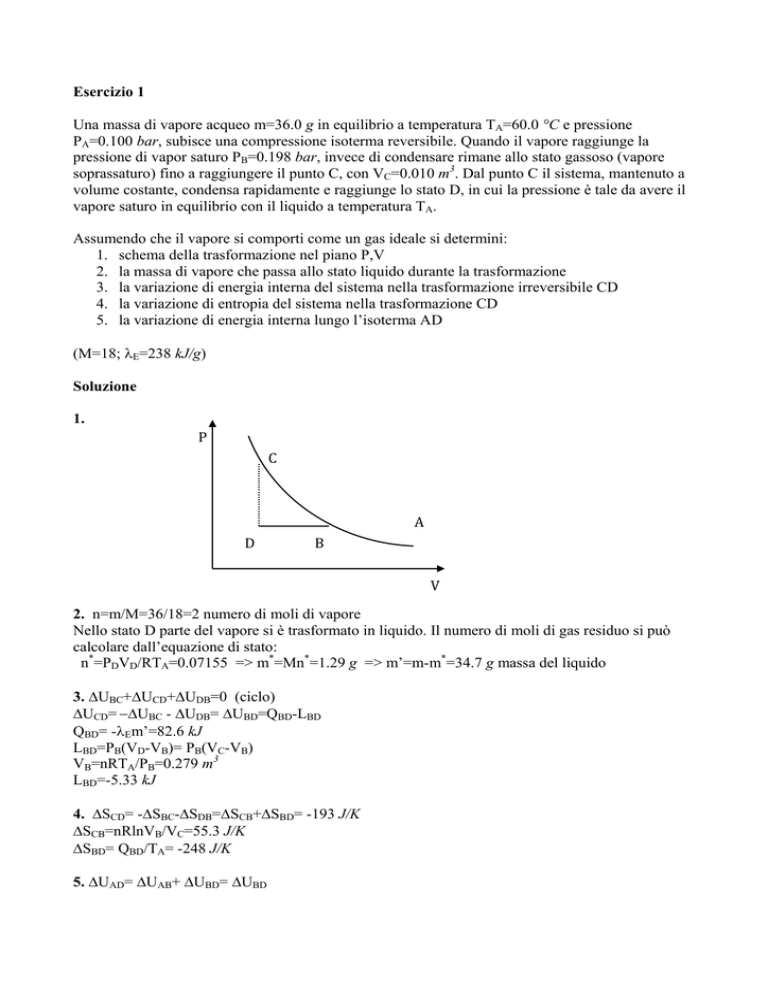
1. schema della trasformazione nel piano P,V
2. la massa di vapore che passa allo stato liquido durante la trasformazione
3. la variazione di energia interna del sistema nella trasformazione irreversibile CD
4. la variazione di entropia del sistema nella trasformazione CD
5. la variazione di energia interna lungo l’isoterma AD
(M=18; E=238 kJ/g)
Soluzione
1.
P
C
A
D
B
V
2. n=m/M=36/18=2 numero di moli di vapore
Nello stato D parte del vapore si è trasformato in liquido. Il numero di moli di gas residuo si può
calcolare dall’equazione di stato:
n*=PDVD/RTA=0.07155 => m*=Mn*=1.29 g => m’=m-m*=34.7 g massa del liquido
3. UBC+UCD+UDB=0 (ciclo)
UCD= UBC - UDB=UBD=QBD-LBD
QBD= -Em’=82.6 kJ
LBD=PB(VD-VB)= PB(VC-VB)
VB=nRTA/PB=0.279 m3
LBD=-5.33 kJ
4. SCD= -SBC-SDB=SCB+SBD= -193 J/K
SCB=nRlnVB/VC=55.3 J/K
SBD= QBD/TA= -248 J/K
5. UAD= UAB+UBD=UBD
Esercizio 2
Tre moli di un gas ideale monoatomico vengono portati dallo stato A allo stato B mediante una
espansione adiabatica nel vuoto. Successivamente, il gas viene portato allo stato C tramite una
compressione adiabatica irreversibile ed infine il gas viene posto a contatto con una sorgente a
temperatura TA e ritorna allo stato iniziale A con una trasformazione isobara irreversibile. Sono dati
la temperatura TA = 300K, la pressione pA = 2.0x105 Pa ed il lavoro compiuto nella trasformazione
BC, WBC = −3.7x104J.
Disegnare il ciclo nei piani PV e TS
Determinare pressione, volume e temperatura dello stato C
Calcolare le variazioni totali di entropia del sistema, dell’ambiente e dell’universo.
Soluzione.
-La trasformazione AB. Questa trasformazione corrisponde ad una espansione adiabatica libera,
dunque il lavoro e’ nullo (l’espansione nel vuoto non richiede lavoro) e il calore scambiato e’ nullo
(la trasformazione e’ adiabatica). Quindi, dal primo principio, abbiamo:
ΔUAB =0
quindi la trasformazione AB e’ anche isoterma, dato che per un gas ideale l’energia interna dipende
solo dalla temperatura: TA = TB = 300K.
-La trasformazione BC. Dato che la compressione e’ adiabatica, QBC = 0, quindi il primo principio
implica che:
WBC = −ΔUBC = ncv(TB − TC )= ncv(TA − TC )
Risolvendo questa relazione rispetto a TC si otiene:
TC = TA – WBC/ncv = 1288.96K
Ora, il volume dello stato C puo essere ricavato dalla relazione pC VC = nRTC , utilizzando il fatto
che pA = pC :
VC = nRTC / pA =0.16m3
-La trasformazione CA. Il gas cede una quantita di calore QCA che puo’ essere calcolata facilmente
perche la trasformazione e’ isobara:
QCA = ncp(TA − TC )= −61666.60J
Questa informazione e’ utile per determinare la variazione di entropia dell’universo per il ciclo. Nel
nostro caso, abbiamo
ΔSu =ΔSgas +ΔSamb
Le tre trasformazioni subite dal gas nel ciclo sono irreversibili, pero’ sommando i contributi risulta
ΔSgas = 0, perche’ corrisponde alla variazione di entropia di un gas per il ciclo (l’entropia e’ una
funzione di stato). Quindi rimane solo da determinare la variazione di entropia dell’ambiente. Essa
viene data dal fatto che la sorgente termica assorbe del calore Q ceduto dal gas, quindi
Q = −QCA = +61666.60J
e la variazione di entropia dell’ambiente (e dell’universo) risulta essere:
ΔSu =ΔSamb =Q/TA = 61666.60J / 300K = 205.56J/K












