richiami sulle variabili aleatorie

RICHIAMI SULLE VARIABILI ALEATORIE
In termini probabilistici una variabile aleatoria è definita dalla sua funzione di probabilità (o
funzione di distribuzione) ovvero dalla funzione di densità di probabilità (è la derivata della prima).
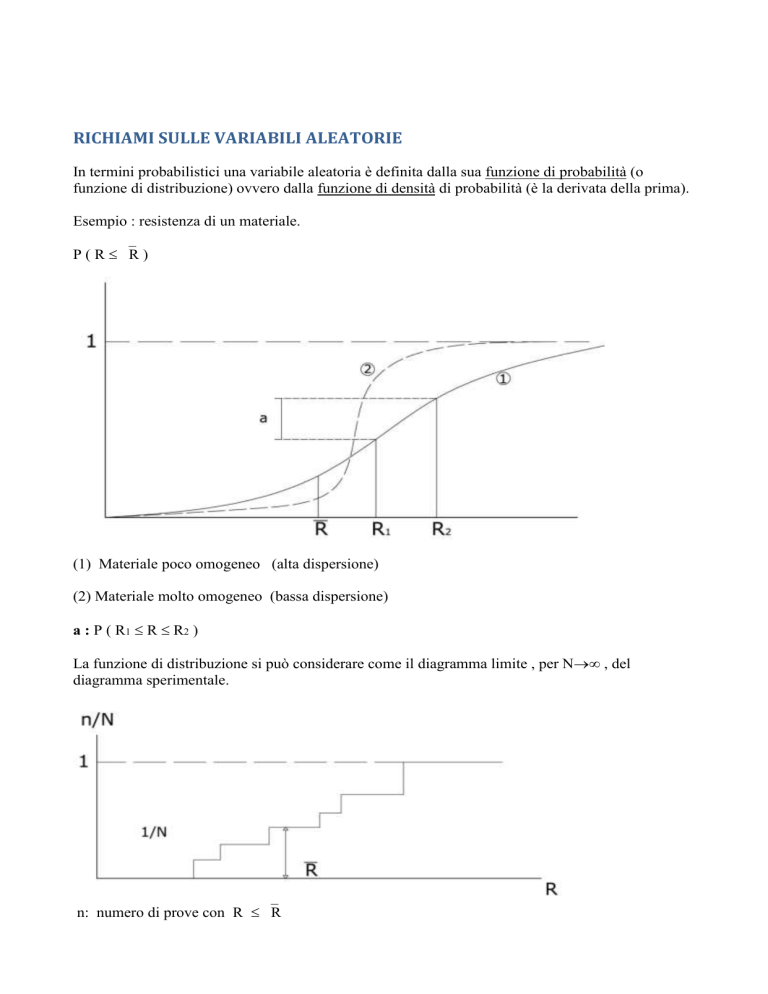
Esempio : resistenza di un materiale.
P ( R  R )
(1) Materiale poco omogeneo (alta dispersione)
(2) Materiale molto omogeneo (bassa dispersione)
a : P ( R1  R  R 2 )
La funzione di distribuzione si può considerare come il diagramma limite , per N , del
diagramma sperimentale.
n: numero di prove con R  R
N: numero di prove totale
Dalla P (R  R ) si ottiene per derivazione la curva di densità P f(R) =
Area tratteggiata : P ( R1  R  R2 )
Area totale = 1
Importanti i momenti del I° e II° ordine delle f (R)
 f ( R) RdR R
 f ( R)( R  R ) dR  S
valore medio
0
2
2
0
varianza (S= deviazione standard)
Disponendo di N prove
n
R0 
 Ri
i
N
n
S2
 ( Ri  R0 ) 2
i
N 1
dP
dR
Frattile di ordine  ( 0    1)
Valore corrispondente probabile ( R  R ) = 
Valore caratteristico di una resistenza f(k)è il frattile di ordine a(di solito 0.05) della
corrispondente distribuzione .
Nel caso delle azioni determinare le distribuzioni è molto complesso per motivi pratici. Inoltre
quando i carichi sono variabili nel tempo, la distribuzione ne va riferita alla “vita” della struttura.
Il frattile è di solito di 0.95. Se si traducono le azioni in un certo punto si ha:
La distanza fra i due frattali copre tutti gli altri fattori di incertezza.
Per distribuzioni normali ( resistenza) :
Per eventi di breve durata ( sismi, vento) si ricorre alla nozione “periodo di ritorno”, cioè
l’intervallo medio di tempo tra due eventi consecutivi di assegnata intensità ( ad es. sisma
distruttivo) oppure vento a 100 km/ora.
Ad esempio sia quella in figura.
La densità corrispondente alle curve di distribuzione.dei massimi annuali delle velocità del vento in
un dato sito ( distribuzione di Gumbel) . Se si considera il frattile di 0.98,
, cioè significa che in
un anno generico si ha solo il 2% di possibilità che venga raggiunto
. ciò significa che il periodo
di ritorno di
è di 1/0.02 =50 anni