Leggi di Gay-Lussac
Consideriamo una trasformazione che coinvolge un gas ideale a pressione costante. In questo caso il
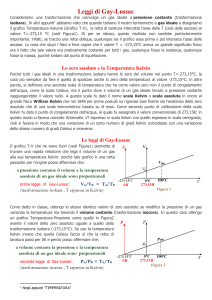
volume V e la temperatura TC, misurata in gradi Celsius, sono legati tra loro dalla relazione: V = V0 (1 + α ·
TC) dove V0 è il volume occupato dal gas a 0 °C. Il coefficiente = 1 / 273.15 °C-1 è praticamente lo
stesso per tutti i gas, purché essi siano lontani dal punto di liquefazione (cioè, siano gas perfetti).
Questa legge prende il nome di prima legge di Gay-Lussac. Dal grafico riportato nella figura sopra
scopriamo che il volume di un gas diventa zero alla temperatura TC = -273,15 °C, ossia allo zero assoluto,
come visto in altri appunti.1 Di per se stesso, questo risultato non sarebbe particolarmente importante: infatti,
se traccio una retta obliqua, qualunque sia il grafico essa prima o poi interseca l’asse delle x. La cosa che stupì
i fisici e fece capire che il valore Tc = -273,15°C aveva un grande significato fisico era il fatto che tale valore
era praticamente costante per tutti i gas, qualunque fosse la sostanza, qualunque fosse la massa, purché
lontani dal punto di liquefazione.
La legge di Gay-Lussac e la Temperatura Kelvin
La legge di Gay-Lussac assume una forma semplificata se la riscriviamo in termini della temperatura in gradi
Kelvin
(TK):
TK=TC +273,15. Infatti, V=V0·(1+TC/273,15) può essere riscritta come
V=V0·(273,15+TC)/273.15, ossia (sapendo che 273,15+T=TK): V = V0·TK/T0 , dove T0 è la temperatura
alla quale il volume del gas è uguale a V0. In altre parole, a pressione costante il volume e la temperatura
assoluta di un gas ideale sono direttamente proporzionali.
Esiste anche una seconda legge dovuta a Gay-Lussac: essa descrive il comportamento di un gas a volume
costante ed è esattamente analoga alla precedente, ossia la pressione p e la temperatura in gradi Celsius
TC sono legate tra loro dalla relazione: p = p0 (1 + α’·TC) dove p0 è la pressione del gas a 0 °C. La costante
’ ha lo stesso valore della costante che abbiamo trovato nella prima legge: ’ = α = 1/273.15 °C-1 .
Anche in questo caso la pressione diventa uguale a 0 a TC=-273,15 °C e la legge può essere riscritta in termini
della temperatura in gradi Kelvin T come p = p0·T/T0, ossia a volume costante la pressione e la
temperatura assoluta di un gas ideale sono direttamente proporzionali.
http://digilander.libero.it/danilo.mauro/temi/gasideali1.html
1
Negli appunti “TEMPERATURA”