Determina per quali valori del parametro k la seguente equazione ammette soluzioni reali e tra loro discordi:
Geometria:
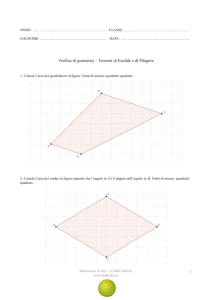
È dato il quadrilatero convesso ABCD, avente AB
AC
AD =4cm;
ed
Calcolare la misura di BD, le
distanze dei vertici B e D dalla diagonale AC e la misura di EF dove E ed F sono i piedi delle perpendicolari condotte da B e
da D ad AC. Condotta infine da B la perpendicolare alla retta DC, e detto H il suo piede, calcolare le misure di BH, CH e DC.
Nel trapezio isoscele ABCD, la cui area misura 36
, l’altezza è della base minore e ciascun lato obliquo misura 5cm.
Calcolare le misure delle basi del trapezio, l’area del triangolo avente per lati la base minore e il prolungamento dei lati
obliqui, la lunghezza del raggio della circonferenza circoscritta a tale triangolo e di quella in esso inscritta.
Determina le condizioni di esistenza della seguente espressione:
Geometria:
Nel triangolo ABC, isoscele sulla base BC, la somma della base con la relativa altezza misura 22cm e l’area misura 60
;
calcola il perimetro del triangolo. Dal baricentro si conduce la parallela a BC che interseca AB e AC rispettivamente in M e
in N. Trova il perimetro di AMN.
Nel trapezio rettangolo ABCD, la base minore DC forma con il lato obliquo BC un angolo di 135°. Sapendo che la somma
delle basi è 11cm e quella dei quadrati dei quattro lati 92
, calcolare le misure delle due basi e le misure dei segmenti
in cui si dividono scambievolmente le due diagonali.
Risolvi le seguenti equazioni, determinandone, quando possibile anche le soluzioni complesse:
Risolvi il seguente sistema:
Senza risolvere le seguenti equazioni, stabilisci il numero di soluzioni reali e complesse, motivando le tue affermazioni:
L’area di un rombo è 84
e del raggio del cerchio inscritto.
Il perimetro di un triangolo rettangolo misura 40cm; trova la sua area, sapendo che la somma dei suoi cateti è di 23cm.
Un triangolo ha un angolo di 45° e uno di 105°, sapendo che il suo perimetro misura
l’area del triangolo.
Risolvi:
. Sapendo che una diagonale supera l’altra di 2cm, trova la lunghezza delle diagonali, del lato
, determina
Geometria:
Il perimetro del trapezio isoscele ABCD circoscritto ad una circonferenza è 80cm; determina la misura del
raggio della circonferenza, sapendo che la base maggiore è tripla della minore.
Trova i lati di un trapezio rettangolo circoscritto ad una circonferenza di raggio 6cm, sapendo che la sua area
è 150
.
Determina l’area di un rettangolo inscritto in una circonferenza, sapendo che il raggio della circonferenza è
e il perimetro del rettangolo è
.
Risolvi le seguenti equazioni, determinandone, dove possibile, anche le soluzioni complesse:
Nelle seguenti equazioni stabilisci il numero di soluzioni reali e complesse, senza risolverle e motivando
le tue affermazioni:
Geometria:
Due corde parallele di una stessa circonferenza sono situate dalla stessa parte rispetto al centro e
misurano rispettivamente 50cm e 78cm. Determina la distanza della corda maggiore dal centro e il
raggio della circonferenza, sapendo che la distanza tra le due corde è di 8cm.
Un parallelogrammo ABCD ha l’angolo di 60° e l’angolo formato dalla diagonale BD con la base AB
è di 45°. Sapendo che AB è
cm, calcola il perimetro del parallelogrammo.
Da un punto A esterno ad una circonferenza di centro O e di raggio
tangente AB. Sapendo che A dista dal centro O
, si conduce una
, calcolare l’area del triangolo AOB e le
diagonali e il lato del rombo equivalente al triangolo, sapendo che il rapporto delle diagonali è .
Trova soluzioni reali e complesse delle seguenti equazioni:
x2 2 x2 1 x4 2 x2 4
0;
x2 1 x2 2
2 x2 x4
x
2
3x 2
3x 2
36 13 2
x 6x 9
x3
8 x 15 5 x 2 8 x 15 3 2 x 0;
2
4
2
x 6 19 x 3 216
Senza risolvere le seguenti equazioni, stabilisci il numero di soluzioni reali e complesse, motivando le tue risposte:
x 4 x 2 5 0;
Geometria:
x 4 5x 2 6 0;
x4 x 0
In un trapezio isoscele i lati obliqui formano angoli di 45° con la base maggiore. Sapendo che il perimetro e
l’area del trapezio sono rispettivamente 8cm e 2 2 cm2 , trovare le basi e il lato obliquo. Dire infine se il
trapezio è circoscrittibile ad una circonferenza e, in caso affermativo, trovare la lunghezza dell’apotema.
Un rombo ha un angolo di 120°. Sapendo che la somma delle sue diagonali è di 30 1 3 cm, trova
perimetro e area del rombo.
La diagonale BD del rettangolo ABCD forma con il lato AB un angolo di 30°. Sapendo che la misura di AB è
radice dell’equazione x 3 4 3 x 2 12 3 x 8 3 0 , trova perimetro e area del
rettangolo.
3
2
Geometria:
In un rombo il cui perimetro misura 200cm,è inscritto un rettangolo la cui area è uguale a 1200
punti medi dei lati del rombo. Trovare le diagonali del rombo.
Il rettangolo ABCD ha la diagonale BD di 30cm e l’area di 432
e i cui vertici sono i
. Dopo aver determinato le misure dei lati AB e AD, si
consideri su BD il punto P tale che DP sia il doppio di PB; condotta da P la perpendicolare alla retta BD, determinare
perimetro e area di ciascuna delle due parti in cui tale perpendicolare divide il rettangolo dato.
I cateti AB e AC di un triangolo rettangolo misurano rispettivamente 36cm e 48cm. Condotta la perpendicolare
all’ipotenusa BC nel suo punto medio M, si indichi con K il suo punto di intersezione con la retta AC. Determinare
perimetro e area del triangolo MCK. Dire infine se il quadrilatero ABMK è inscrittibile e circoscrittibile e, in caso
affermativo, determinare il raggio delle relative circonferenze.
Data una circonferenza di centro O, il cui raggio misura 6cm, sia P un punto tale che OP=10cm. Condotta da tale punto
una retta secante la circonferenza, siano H e K i suoi punti di intersezione con la circonferenza stessa, con K compreso tra
H e P. sapendo che PK=6cm, determinare PH, la distanza di O dalla secante considerata e la lunghezza del segmento di
tangenza condotto da P alla circonferenza.
Risolvi:
Geometria:
Dimostra che se in un trapezio ABCD, rettangolo in A e in D, le diagonali sono perpendicolari, i triangoli DAB e ACB sono
simili; imposta quindi la proporzione fra i lati corrispondenti.
Un punto esterno a una circonferenza dista dal centro 68cm. Dal punto sono condotte una tangente e una secante la cui
parte esterna misura 40cm. Calcola le misure della tangente e dell’intera secante, sapendo che il raggio del cerchio
misura 32cm.
In un rettangolo la base è
della diagonale; determina il suo perimetro sapendo che la somma dei quadrati costruiti
sulla diagonale e sull’altezza del rettangolo è 1201
.
Nel trapezio rettangolo ABCD la base minore è di quella maggiore e l’altezza è i
l’area di ABCD è 432
diagonali intersecandosi.
della base minore. Sapendo che
, calcola la misura dei lati e delle diagonali del trapezio e la misura delle parti in cui si dividono le