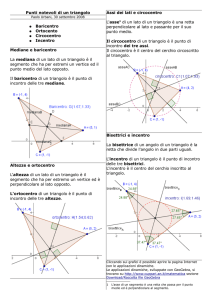
PUNTI NOTEVOLI DI UN TRIANGOLO
-
Disegnate un triangolo qualsiasi e cliccate con il destro su proprietà. Nella casella stile
ingrossate lo spessore della linea fino a 5 e portate a zero il riempimento
Tracciate le altezze del triangolo e l’ortocentro (chiamatelo O) utilizzando lo stesso colore
Tracciate gli assi del triangolo e il circocentro (chiamatelo K) utilizzando un altro colore
Tracciate le mediane del triangolo e il baricentro (chiamatelo G) utilizzando un altro colore
Tracciate le bisettrici del triangolo e l’incentro (chiamatelo I) utilizzando un altro colore
Tracciate la retta di Eulero
Nascondete ora altezze, bisettrici mediane, assi e punti medi
Fate variare gli angoli e i lati del triangolo muovendo i vertici con il mouse e quindi rispondete
alle domande:
1) Quando l’ortocentro è interno al triangolo?...................................................................
2) Quando l’ortocentro è esterno al triangolo?...................................................................
3) Quando l’ortocentro coincide con un vertice del triangolo?....................................................
4) Se l’ortocentro è interno il circocentro è ………………………… il baricentro è
………………. e l’incentro è …………………… Se l’ortocentro è esterno il circocentro è
………………………… il baricentro è ………………. e l’incentro è ……………………
Se l’ortocentro è su un vertice il circocentro è ………………………… il baricentro è
………………. e l’incentro è ……………………
In conclusione baricentro e incentro sono sempre ………… mentre ortocentro e circocentro
sono interni se il triangolo è ………………., esterni se il triangolo è ………………………..,
rispettivamente sul vertice dell’angolo ………….….. e sull’……………… se il triangolo è
……………………
5) E’ possibile che il punto I appartenga alla retta di Eulero e se sì quando?................................
6) Se sposto un vertice del triangolo in modo da far coincidere G con K che cosa succede a I e
O?.................................... Com’è il triangolo che si ottiene? ………………………………
E la retta di Eulero?..................................
7) Misurate la distanza OG e la distanza KG. Fate variare la posizione dei vertici del triangolo.
C’è una relazione tra le due distanze e se sì quale? .......................
Costruite ora la circonferenza passante per i piedi delle tre altezze del triangolo (cioè per i punti
di intersezione tra le altezze e i lati a cui sono relative) (usate lo strumento mostra/nascondi per
mostrale di nuovo). Tale circonferenza è detta circonferenza di Eulero. Sapreste individuare
degli altri punti particolari del triangolo per cui passa questa circonferenza?...........................