GEOMETRIA EUCLIDEA – Triangoli
LEZIONI
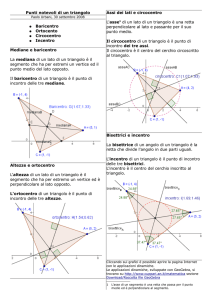
Punti notevoli di un triangolo
Dato il generico triangolo ABC, i suoi punti notevoli sono così definiti:
BARICENTRO:
Definizione
E’ il punto d’incontro delle mediane;
Proprietà caratteristiche
Divide ogni mediana in due parti tali che quella che
ha per estremo il vertice è doppia della restante.
Figura 1 - Baricentro
INCENTRO
Definizione
E’ il punto d’incontro delle bisettrici degli angoli;
Proprietà caratteristiche
− E’ equidistante dai lati.
− E’ il centro della circonferenza inscritta nel
triangolo.
Figura 2 - Incentro
CIRCOCENTRO
Definizione
E’ il punto d’incontro degli assi.
Proprietà caratteristiche
− E’ equidistante dai vertici del triangolo.
− E’ il centro della circonferenza circoscritta al
triangolo.
Figura 3 - Circocentro
Prof. Salvatore Scialpi - www.numerica.altervista.org
Pag. 1/2
GEOMETRIA EUCLIDEA – Triangoli
ORTOCENTRO
Definizione
E’ il punto d’incontro delle altezze del triangolo.
Figura 4 - Ortocentro
EXINCENTRO
Definizione
Ogni triangolo ne ammette tre: uno per ciascun
vertice. Gli exincentro sono definiti come i punti
d’incontro della bisettrice interna di un angolo e
delle bisettrici esterne degli altri due.
Proprietà caratteristiche
E’ il centro della circonferenza exinscritta, cioè
tangente ad un lato del triangolo ed ai
prolungamenti degli altri due lati.
Figura 5 - Exincentro
Prof. Salvatore Scialpi - www.numerica.altervista.org
Pag. 2/2