Componenti di un vettore Sia dato un vettore v, in sistema di assi

Componenti di un vettore
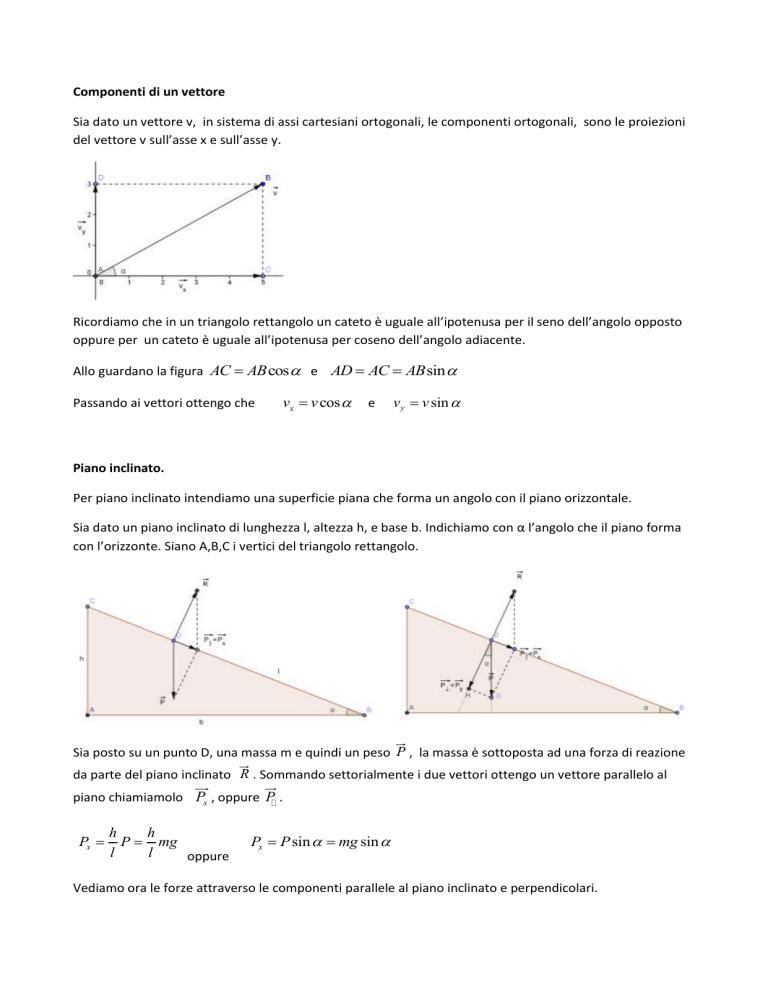
Sia dato un vettore v, in sistema di assi cartesiani ortogonali, le componenti ortogonali, sono le proiezioni
del vettore v sull’asse x e sull’asse y.
Ricordiamo che in un triangolo rettangolo un cateto è uguale all’ipotenusa per il seno dell’angolo opposto
oppure per un cateto è uguale all’ipotenusa per coseno dell’angolo adiacente.
Allo guardano la figura AC  AB cos  e AD  AC  AB sin 
Passando ai vettori ottengo che
vx  v cos 
e
v y  v sin 
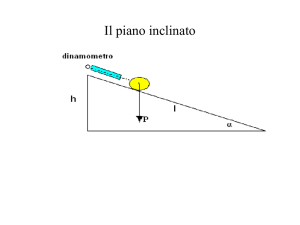
Piano inclinato.
Per piano inclinato intendiamo una superficie piana che forma un angolo con il piano orizzontale.
Sia dato un piano inclinato di lunghezza l, altezza h, e base b. Indichiamo con α l’angolo che il piano forma
con l’orizzonte. Siano A,B,C i vertici del triangolo rettangolo.
Sia posto su un punto D, una massa m e quindi un peso P , la massa è sottoposta ad una forza di reazione
da parte del piano inclinato R . Sommando settorialmente i due vettori ottengo un vettore parallelo al
piano chiamiamolo Px , oppure P .
Px 
h
h
P  mg
l
l
oppure
Px  P sin   mg sin 
Vediamo ora le forze attraverso le componenti parallele al piano inclinato e perpendicolari.
Sul piano inclinato che chiamiamo x, agisce la componente del peso
x: Fx  Px  mg sin   mg
h
l
sul piano y agiscono due forze uguali ed opposte R e la componente perpendicolare del peso Py
y:
Fy  R  Py  R  mg cos   0 da cui R  mg cos   mg
b
l
Dimostrazione:
Se io scompongo il vettore P ,in due vettori (componenti) uno parallelo al piano Px e un altro
perpendicolare Py , ottengo che la componente Py , genera una reazione del piano uguale ed opposta R .
Considerando il piano inclinato e i le componenti dei vettori si vengono a formare due triangoli rettangoli
simili ABC e DHG.
Sono simili perché hanno uguale l’angolo retto e l’angolo α.
ˆ  DBA
ˆ 
GDH
(Dato che la somma degli angoli interni in un triangolo è pari a 180°,
ˆ  90  HDB
ˆ  90  (90   )   .)
ˆ  90   , e dato che HDB
ˆ  90 , abbiamo GDH
GDD
P h
HG CA

sostituendo ho che x 
DG CB
P l
Py b
HD BA

2) Allora
sostituendo ho che

DG CB
P l
1) Allora
Px 
h
h
P  mg
l
l
Py 
b
b
P  mg
l
l
Oppure ricordando le proprietà dei triangoli rettangoli e le componenti. (vedi sotto)
Px  P sin   mg sin 
e Py  P cos   mg cos 
Questo perché la componente x è opposto all’angolo α, la componente y è adiacente.