PROGETTO RETI DI TELECOMUNICAZIONI
30-09-2004
Esercizio 1
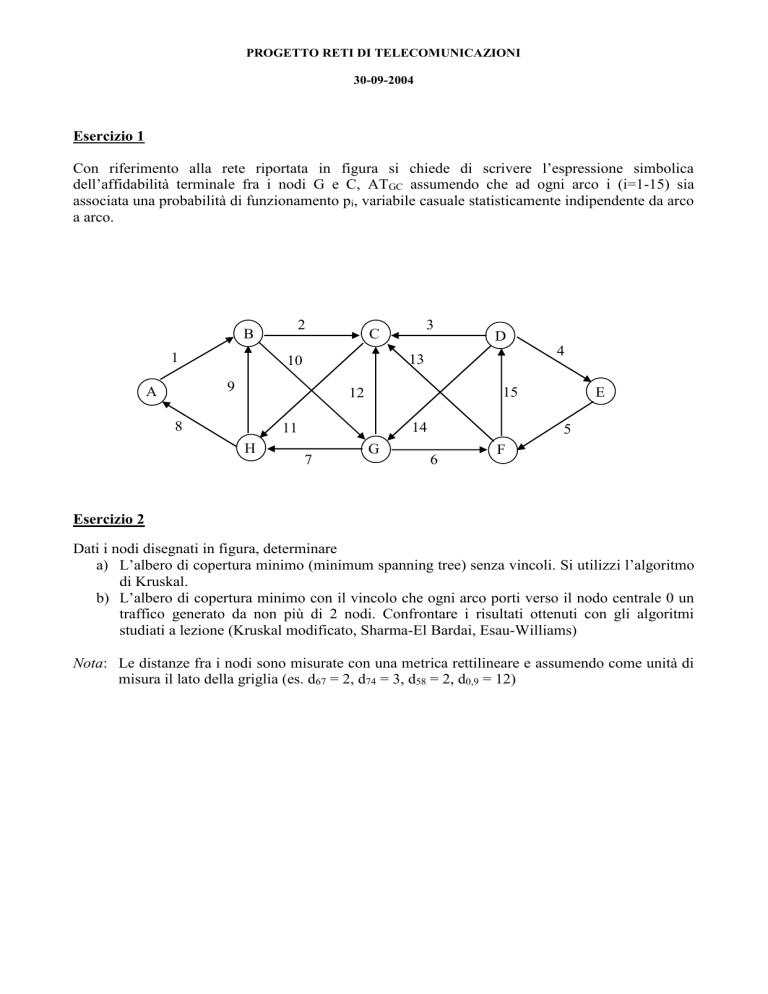
Con riferimento alla rete riportata in figura si chiede di scrivere l’espressione simbolica
dell’affidabilità terminale fra i nodi G e C, ATGC assumendo che ad ogni arco i (i=1-15) sia
associata una probabilità di funzionamento pi, variabile casuale statisticamente indipendente da arco
a arco.
2
B
1
4
15
12
8
14
11
H
D
13
10
9
A
3
C
7
G
E
5
6
F
Esercizio 2
Dati i nodi disegnati in figura, determinare
a) L’albero di copertura minimo (minimum spanning tree) senza vincoli. Si utilizzi l’algoritmo
di Kruskal.
b) L’albero di copertura minimo con il vincolo che ogni arco porti verso il nodo centrale 0 un
traffico generato da non più di 2 nodi. Confrontare i risultati ottenuti con gli algoritmi
studiati a lezione (Kruskal modificato, Sharma-El Bardai, Esau-Williams)
Nota: Le distanze fra i nodi sono misurate con una metrica rettilineare e assumendo come unità di
misura il lato della griglia (es. d67 = 2, d74 = 3, d58 = 2, d0,9 = 12)
6
7
8
9
5
4
2
3
1
10
11
12
0
Esercizio 3
In un edificio governativo si vuole disporre di un collegamento wireless esteso a tutti i piani. A tal
scopo è disponibile un insieme I di punti dove installare delle antenne di trasmissione/ricezione. La
copertura è valutata su un insieme J di test point, che devono essere raggiunti qualunque sia la
scelta delle antenne. È data la distanza dij di ogni antenna i da ogni test point j, e si sa che un test
point è coperto da un’antenna se la distanza tra i due non supera un certo parametro D. Per
raggiungere un testpoint j, un’antenna i deve emettere un segnale di potenza pari a kdij, che è
sufficiente a coprire anche i test point a distanza inferiore. Quindi la potenza di un’antenna è quella
necessaria a coprire il più lontano tra i test point assegnati ad essa.
a) Formulare un modello di Programmazione Lineare Intera per risolvere il problema di coprire
tutti i testpoint in modo da minimizzare la potenza massima emessa dalle antenne;
b) Come cambia il modello se si vuole minimizzare la somma delle potenze emesse?
c)
Supporre che al modello del punto b) si aggiunga il vincolo secondo cui ogni antenna non
può coprire più di p testpoint. Scrivere il vincolo lineare corrispondente.












