MATEMATICA
CL. 3
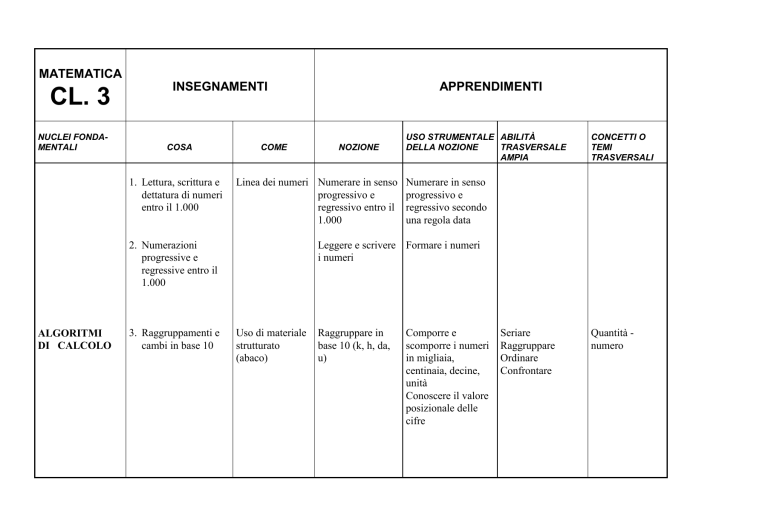
NUCLEI FONDAMENTALI
INSEGNAMENTI
COSA
1. Lettura, scrittura e
dettatura di numeri
entro il 1.000
COME
3. Raggruppamenti e
cambi in base 10
NOZIONE
Linea dei numeri Numerare in senso
progressivo e
regressivo entro il
1.000
2. Numerazioni
progressive e
regressive entro il
1.000
ALGORITMI
DI CALCOLO
APPRENDIMENTI
USO STRUMENTALE ABILITÀ
DELLA NOZIONE
TRASVERSALE
AMPIA
CONCETTI O
TEMI
TRASVERSALI
Numerare in senso
progressivo e
regressivo secondo
una regola data
Leggere e scrivere Formare i numeri
i numeri
Uso di materiale
strutturato
(abaco)
Raggruppare in
base 10 (k, h, da,
u)
Comporre e
scomporre i numeri
in migliaia,
centinaia, decine,
unità
Conoscere il valore
posizionale delle
cifre
Seriare
Raggruppare
Ordinare
Confrontare
Quantità numero
4. Confronto di
quantità usando i
segni > < =
Ordinamento di Conoscere e usare
numeri dal
i segni > < =
minore al
maggiore e
viceversa
Linea dei numeri
Saper confrontare
dei numeri
5. Proprietà
operazioni:
commutativa,
associativa
dell’addizione;
invariantiva della
sottrazione e
commutativa della
moltiplicazione
Uso dei regoli,
Utilizzare le
degli
proprietà
schieramenti e di
materiale vario
Calcoli orali e
scritti
Sveltire e
semplificare il
calcolo.
Formare numeri
6. Eseguire addizioni e
sottrazioni in
colonna con il
cambio, con numeri
interi
Incolonnamenti Eseguire addizioni
di numeri
e sottrazioni in
rispettando il
colonna
valore
posizionale delle
cifre (tabella)
7. Moltiplicazioni con
una cifra al
Schieramenti e
moltiplicatore con
calcolo
numeri interi.
Moltiplicazioni per
10 - 100 - 1000
Eseguire
moltiplicazioni
con una e/o due
cifre al
moltiplicatore
Utilizzare le
operazioni di
addizione,
sottrazione,
moltiplicazione e
divisione per
risolvere problemi
matematici
Usare strategie.
Consolidare le
abilità del calcolo
mentale mediante
strategie
appropriate
Usare materiali
8. Divisioni con una
Distribuzioni cifra al divisore, con raggruppamenti
numeri interi.
Divisioni per 10 100 – 1000
Eseguire divisioni
con una cifra al
divisore
9. Significato del
numero zero e del
numero uno e loro
comportamento
nelle quattro
operazioni
10.Numeri frazionari frazione
complementare.
PROBLEMI
MATEMATICI
Piegatura di fogli
di carta e
Concetto di
manipolazioni di frazione
insiemi d’oggetti
1. Lettura e
Analisi del testo
comprensione del
di un problema
testo di un problema
matematico
individuando i dati
inutili, mancanti,
contradditori.
Cogliere il dato e
la domanda
Acquisire il
Saper frazionare
concetto di frazione
Comprendere il
Leggere e
testo di un problema comprendere un
testo
Identificare
situazioni
problematiche e
descriverle
Selezionare le
informazioni
Problem solving
2. Individuazione e
applicazione di
strumenti e
operazioni utili per
la soluzione di
problemi con una
domanda e una
operazione e con
due domande e due
operazioni
Diagrammi di
flusso,
diagrammi ad
albero,
diagrammi di
Venn,
operazioni,
tabelle
3. Lettura di
un’immagine, di un
grafico, di una
tabella, di un
algoritmo ed
elaborazione del
testo di un problema
GEOMETRIA
1. Forme geometriche, Osservazione
solidi principali e
della realtà
figure piane che li
geometrica
delimitano
Conoscere le varie Uso appropriato
rappresentazioni. delle 4 operazioni
per risolvere i
problemi
Utilizzare i vari
strumenti in
diverse situazioni.
Costruire un testo
Lettura di
un’immagine e di
un grafico
Conoscere le
principali forme
geometriche
Riconoscere e
disegnare le
principali forme
geometriche
Quantità numero
Osservare lo spazio Concetto di
intorno a noi
spazio
2. Vari tipi di linee:
aperte, chiuse, rette
semirette, spezzate,
curve, miste
3. La simmetria
4. Poligoni e non
poligoni
Osservazione
Conoscere vari tipi Riconoscere e
delle figure
di linee
classificare vari tipi
geometriche
di linee
nella realtà,
disegno di linee e
loro
classificazione
Percorsi
Riconoscere e/o
costruire l’asse di
simmetria di una
figura, seguendo
le istruzioni date
Realizzare figure
geometriche con
varie tecniche.
Distinguere
poligoni e non
poligoni
Disegnare,
costruire,
classificare
figure
geometriche
piane
Riconoscere,
disegnare,
classificare,
costruire poligoni
LOGICA
SISTEMI DI
MISURA
1. Acquisizione di
una
terminologia
appropriata
relativa a
numeri, figure e
relazioni
1. Utilizzo di misure
non convenzionali
(oggetti, parti del
corpo)
Uso di materiali
e schede
appositamente
predisposti
Misurazioni,
confronti
AGGIORNATO AL 30 SETTEMBRE 2007
Uso appropriato
del linguaggio
specifico
disciplinare
Conoscere sistemi Misurare con
di misura non
campioni non
convenzionali
convenzionali
Misurare
Misura