Prova scritta di Misure Elettriche NO del 28_febbraio_2013
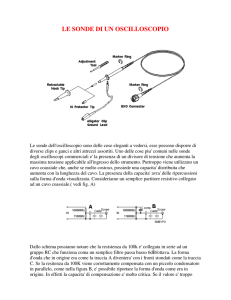
1. Spiegate come funziona la sonda compensata dell’oscilloscopio e perché essa è preferibile ad un semplice cavo
coassiale. Sotto quale ipotesi la sonda non distorce la forma d’onda del segnale? Qual è l’impedenza di ingresso della
sonda compensata? Come si comporta il sistema sonda+oscilloscopio (si richiede la dimostrazione analitica)? Si
misura la resistenza della sonda ottenendo le seguenti 3 letture: 8.99 M, 9.01 M, 9.00 M. Qual è la misura
dell’attenuazione di tale sonda compensata se l’impedenza di ingresso dell’oscilloscopio è costituita dal parallelo di
una resistenza pari a 1M 1% e di una capacità pari a 30 pF 1%?
2. Un sensore con resistenza al platino è utilizzato per misurare temperature tra 0 e 200 °C. Se la sua resistenza RT, in
, alla temperatura T, in °C, è data da R T=R0(1+T+T2) ed R0=100.0 , R100=138.50 ed R200=175.83 calcolare
, e la non linearità a 100 °C come percentuale del fondo scala. Una volta che si è ricavato il modello, determinare
le incertezze nelle misure di R100 ed R200 se l’incertezza nella misura della temperatura è pari all’1%, R0 presenta
anch’esso un’incertezza dell’1% mentre e si possono supporre con incertezza trascurabile.
3. Si ha a disposizione un convertitore analogico/digitale del tipo in figura seguente, con le seguenti caratteristiche:
fondo scala: 10V; risoluzione 10 mV
Di cosa si tratta? Descrivere funzionamento e cause di incertezza nel caso in cui si misuri una tensione continua di 3V
nominali. Dopo aver illustrato la relazione ingresso/uscita di un ADC ideale, chiarire il significato degli errori di
quantizzazione e di conversione negli ADC.
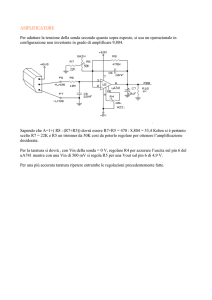
4. Dopo aver disegnato e commentato lo schema circuitale di un voltmetro analogico AC a doppia semionda per la
misura del valore di picco, si misuri il valore di picco della sinusoide mostrata in figura seguente sullo schermo di un
oscilloscopio; quale sarà il valore dell’incertezza dovuta all’errore legato alla frequenza del segnale se C = 30 pF
1% ed R = 1M 1%? Come migliorare tale incertezza? Quali sono le altre incertezze nel caso reale e come
minimizzarle? Che lettura sarà mostrata sul display e perchè?
1. La media di un campione casuale di 50 voti in matematica, su un totale di 200, è di 75, e lo scarto quadratico medio
vale 10. (a) Quali sono i limiti di confidenza al 95% della stima della media dei 200 voti? (b) Con quale grado di
confidenza potremo dire che la media dei 200 voti è di 751?
2. Sia (X1, X2, ..., Xn) un campione casuale di una v.a. normale X con media e varianza 100. Sia inoltre
H 0 : 50
H 1 : 1 50
Sia infine l’ampiezza del campione n=25. Come procedura decisionale si utilizza la regola di scartare H0 se x 52 .
(a) Si ricavi la probabilità di scartare H0 in funzione di (>50). (b) Si ricavi la probabilità dell’errore del I tipo.
(c) Si ricavi la probabilità dell’errore del II tipo per 1=53 e per 1=55. Commentare le soluzioni anche
avvalendosi di grafici opportuni.
3. In 200 lanci di una moneta si osservano 115 teste e 85 croci. Provate, con un test chi-quadro di adattamento l’ipotesi
che la moneta è buona usando un livello di significatività dello 0.05 e dello 0.01. Se usassimo l’approssimazione
normale alla distribuzione binomiale, e dunque dopo aver determinato media e varianza di questa distribuzione, a
che conclusioni si arriva con un’test delle ipotesi a due code sulla bontà della moneta per gli stessi livelli di
significatività?