Introduzione alla Statistica e al Calcolo delle probabilità - Milano
Prova scritta
30 Gennaio 2008
Esercizio 1
Un’indagine su un campione di 200 coppie sposate prende in esame il reddito annuale della coppia in
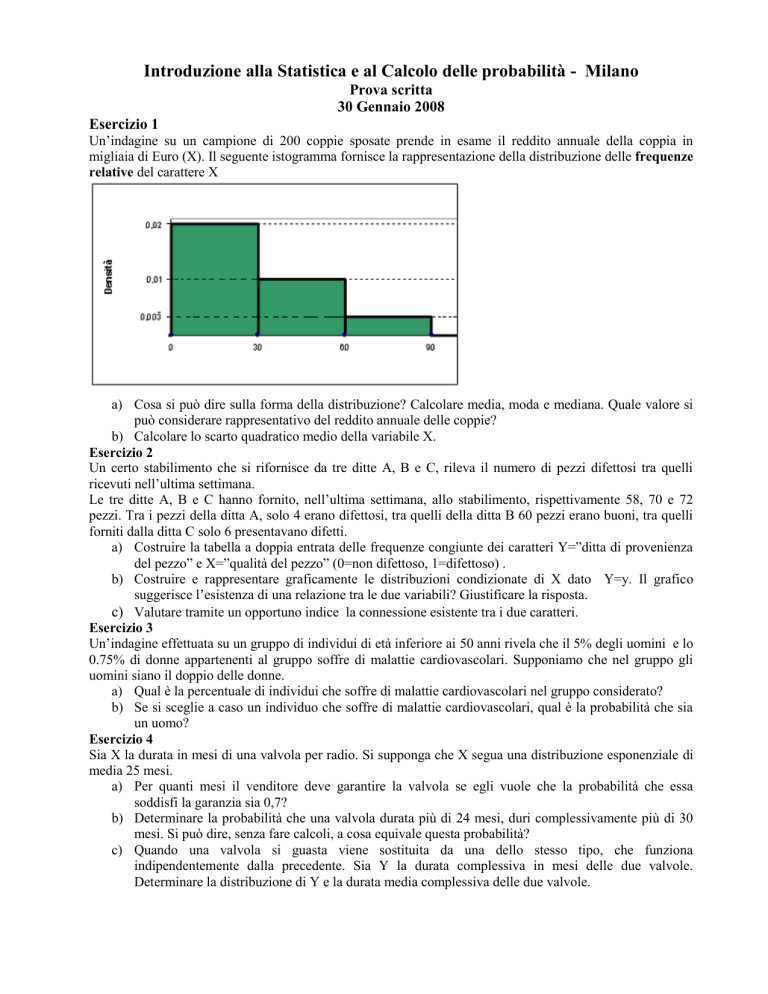
migliaia di Euro (X). Il seguente istogramma fornisce la rappresentazione della distribuzione delle frequenze
relative del carattere X
a) Cosa si può dire sulla forma della distribuzione? Calcolare media, moda e mediana. Quale valore si
può considerare rappresentativo del reddito annuale delle coppie?
b) Calcolare lo scarto quadratico medio della variabile X.
Esercizio 2
Un certo stabilimento che si rifornisce da tre ditte A, B e C, rileva il numero di pezzi difettosi tra quelli
ricevuti nell’ultima settimana.
Le tre ditte A, B e C hanno fornito, nell’ultima settimana, allo stabilimento, rispettivamente 58, 70 e 72
pezzi. Tra i pezzi della ditta A, solo 4 erano difettosi, tra quelli della ditta B 60 pezzi erano buoni, tra quelli
forniti dalla ditta C solo 6 presentavano difetti.
a) Costruire la tabella a doppia entrata delle frequenze congiunte dei caratteri Y=”ditta di provenienza
del pezzo” e X=”qualità del pezzo” (0=non difettoso, 1=difettoso) .
b) Costruire e rappresentare graficamente le distribuzioni condizionate di X dato Y=y. Il grafico
suggerisce l’esistenza di una relazione tra le due variabili? Giustificare la risposta.
c) Valutare tramite un opportuno indice la connessione esistente tra i due caratteri.
Esercizio 3
Un’indagine effettuata su un gruppo di individui di età inferiore ai 50 anni rivela che il 5% degli uomini e lo
0.75% di donne appartenenti al gruppo soffre di malattie cardiovascolari. Supponiamo che nel gruppo gli
uomini siano il doppio delle donne.
a) Qual è la percentuale di individui che soffre di malattie cardiovascolari nel gruppo considerato?
b) Se si sceglie a caso un individuo che soffre di malattie cardiovascolari, qual è la probabilità che sia
un uomo?
Esercizio 4
Sia X la durata in mesi di una valvola per radio. Si supponga che X segua una distribuzione esponenziale di
media 25 mesi.
a) Per quanti mesi il venditore deve garantire la valvola se egli vuole che la probabilità che essa
soddisfi la garanzia sia 0,7?
b) Determinare la probabilità che una valvola durata più di 24 mesi, duri complessivamente più di 30
mesi. Si può dire, senza fare calcoli, a cosa equivale questa probabilità?
c) Quando una valvola si guasta viene sostituita da una dello stesso tipo, che funziona
indipendentemente dalla precedente. Sia Y la durata complessiva in mesi delle due valvole.
Determinare la distribuzione di Y e la durata media complessiva delle due valvole.












