Disequazioni

Disequazioni
Una disequazione è una disuguaglianza fra due espressioni letterali per le quali si cercano i
valori di una o più lettere, le incognite, che la rendono vera ( deve essere precisato l’insieme
numerico in cui si cercano le soluzioni )
Es. x2+1=0 non ha soluzioni in R, ma ha ben due soluzioni in C.
x-1=0 nell’insieme dei numeri reali ha una soluzione, in RxR è soddisfatta da infiniti punti, che
costituiscono una retta parallela all’asse y.
x-1>0 nell’insieme dei numeri reali rappresenta una semiretta privata dell’origine, in RxR è un
semipiano privato della retta che è la frontiera.
I valori che sostituiti all’incognita verificano la disequazione sono le soluzioni della disequazione.
Noi ci limiteremo a disequazioni con una sola incognita e cercheremo le soluzioni nell’insieme dei
numeri reali ( perché non nell’insieme dei complessi? Il campo complesso non è ordinato…….)
Soluzione è ogni numero reale che verifica la disuguaglianza
Risolvere una disequazione significa trovare la totalità delle soluzioni
Una disequazione, in casi particolari, può essere :
identica: soddisfatta per ogni valore attribuito all’indeterminata che non faccia perdere significato
alle espressioni che in essa intervengono
mai vera: quando la disuguaglianza non è mai verificata per alcun valore attribuito
all’indeterminata
Due disequazioni si dicono equivalenti tra loro se sono soddisfatte dagli stessi valori
dell’indeterminata
Principi di equivalenza:
1° Principio di equivalenza:
A>B↔A+M>B+M
M è una qualunque espressione definita in tutto R
Dal primo principio si deduce che ogni espressione può essere scritta nella forma equivalente
C>0 C<0 C≤0 C≥0
2° Principio di equivalenza
Se M è una espressione sempre positiva
A>B↔A*M>B*M
Se M è una espressione sempre negativa
A>B↔A*M<B*M
→Ma vi sono altri principi di equivalenza?
Due principi sono particolarmente utili, ma valgono solo se le espressioni A, B sono positive:
A>0 B>0
A>B ↔1/A<1/B
A≥0 B≥0
A>B↔An>Bn
n positivo
Disequazioni di primo grado
forma normale ax+b>0 o ax+b<0 ( considero le disuguaglianze strette perché le altre sono
riconducibili ad una equazione e ad una diseguaglianza “stretta” )
Considero la prima ax+b>0
se a>0
x>-b/a
se a<0
x<-b/a
se a=0 dipende da b
3x+1>0→x> -1/3
-3x-1>0→x< -1/3
x+3>x→0> -3 sempre verificata per ogni x reale
N.B: se il coefficiente dell’incognita è variabile ( nell’equazione compaiono altre lettere, i
parametri), sarà necessario esaminare tutte le possibilità.
(2h-1)x>h
Se h>1/2
Se h<1/2
Se h=1/2
con h reale
x>h/(h-1)
x<h/(h-1)
la disequazione diventa 0>1/2 mai verificata
(2h-1)x>k
Se h>1/2
Se h<1/2
Se h=1/2
con h, k reale
x>k/(h-1)
x<k/(h-1)
la disequazione diventa 0>k mai verificata se k≥0
Sempre verificata se k<0
Metodo grafico
ax  b  y
ax+b>0 è riconducibile a 
y  0
y=ax+b è una retta, e devo trovare le ascisse dei punti della retta che stanno sopra l’asse x
( nel caso y<0 cercherò i punti della retta sotto l’asse x )
È evidente che ax+b=0 fornisce l’ascissa del punto di intersezione con l’asse x
Il metodo grafico, in questo caso, può sembrare più lento del metodo puramente algebrico, se però
devo risolvere un problema come il seguente:
Trova il massimo, al variare di a reale, dei seguenti numeri espressi in funzione di a
2a-1 ; 3a-2 ; a+1 ; 5
può essere consigliabile
Disequazioni di secondo grado
Forma normale ax2+bx+c>0 o ax2+bx+c<0
Per ricavare le soluzioni sfrutto la rappresentazione grafica di y= ax2+bx+c che rappresenta una
parabola con asse parallelo all’asse y
 y  ax 2  bx  c
Come prima essa è riconducibile a 
y  0
Ricordo in particolare che il segno di a è legato alla concavità della parabola
ax2+bx+c=0 fornisce le ascisse dei punti di intersezione della parabola con l’asse x
un sommario schizzo della parabola che rispetta queste due informazioni permette di ricavare ( anzi
di vedere ) le soluzioni della disequazione
Invece della rappresentazione grafica potrebbe essere usata una regola, da mandare a memoria,
suddivisa nei casi Δ>0
Δ<0 Δ=0
ma la rappresentazione grafica può aiutare molto a ricordarla………
Sistemi di disequazioni
E’ costituito da più disequazioni e si devono cercare i valori di x che soddisfano simultaneamente le
disequazioni
La soluzione del sistema è l’intersezione delle soluzioni delle singole disequazioni
Per risolvere un sistema
1))Risolvo separatamente le singole disequazioni
2)Rappresento le soluzioni delle singole disequazioni su righe distinte di un grafico
3)Cerco le eventuali soluzioni comuni ( cioè i valori reali evidenziati in ogni riga del grafico)
Se non ve ne fossero, il sistema è impossibile.
→Se una disequazione del sistema è impossibile, posso evitare di risolvere le altre perché il sistema
è…………
Disequazioni frazionarie
Forma normale
A x 
<0
Bx 
Consideriamo la seconda
A x 
>0
Bx 
A x 
>0
Bx 
Essa è equivalente all’unione dei due sistemi
A  0

B  0
A  0
o 
B  0
Oppure
Studio il segno dei singoli fattori
A(x)>0
A(x)=0 e per esclusione deduco A(x)<0
B(x)>0
B(x)=0 e per esclusione deduco B(x)<0
Compilo un grafico, visualizzando il segno di A(x) e di B(x) su distinte righe del grafico
Deduco con la regola dei segni, il segno del quoziente, e in base al senso della disequazione iniziale
sceglierò le soluzioni
→Queste tecniche funzionano anche nel caso A(x) * B(x)>0
→Nel caso di disequazioni di grado superiore al secondo ci si potrà ricondurre a un prodotto
scomponendo il primo membro della disequazione ( al secondo membro vi deve essere 0 )
→La seconda delle due tecniche illustrate è particolarmente conveniente nel caso di espressioni che
presentano più fattori
Casi particolari di disequazioni di grado superiore al secondo:
ricordando i grafici di y=xn nel caso
n pari
∕
n dispari
si può dedurre facilmente la soluzione di xn>a
→Può valere il seguente principio di equivalenza A>B↔An>Bn nel caso n dispari?
E nel caso di n pari? Se non vale, come può essere rettificato?
Se A>0 e B>0 allora A>B↔An>Bn
X4<16  x<2  -2<x<2
X4 >16  x>2  x<-2 o x>2
X3>8  x>2
Disequazioni “trinomie”
Ax2n+bxn+c >0
Sostituire xn con t
Si trova una disequazione di 2° in t che deve essere risolta
Successivamente si ricavano dai valori di t i valori di x
Potenze
An
se n è pari è sempre positivo o nullo
se n è dispari An ha lo stesso segno di A
quindi An>0
se n è pari diventa A≠0
n
quindi A >0
se n è dispari diventa A>0
prova ad usare anche gli altri segni di confronto quindi An<0
ecc…
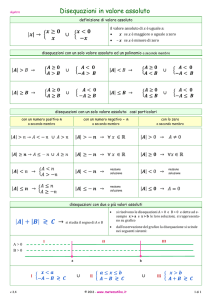
Definizione di valore assoluto
│A│=

A se A≥0
-A se A≤0
→Dalla definizione si deduce che è possibile esprimere il valore assoluto con soli valori relativi, a
patto di conoscere il segno del suo argomento
→Se devo risolvere una equazione o una disequazione contenente un valore assoluto basterà
esprimerle con soli valori relativi ( considerando evidentemente tutti i casi possibili…….)
In genere una equazione o una disequazione contenente un valore assoluto è equivalente all’unione
di due sistemi
A  0
A  0
│A│>B
equivalente 
o 
 A  B
A  B
→Il valore assoluto è sempre una quantità positiva o nulla: questo rende particolarmente facile
risolvere disequazioni o equazioni del tipo │A│>B │A│=B con B negativo o nullo
→│A│ può essere interpretato come distanza del numero A dall’origine
→Nel caso B>0 la disequazione │A│>B
→Nel caso B>0
│A│<B
è equivalente a A<-B o A>B
 A  B
è equivalente a 
A  B
→ Nel caso sia presente nell’espressione più di un valore assoluto con argomenti diversi, si dovrà
procedere ad un esame preliminare del segno dei singoli argomenti ( studiando ad esempio ove i
singoli argomenti sono positivi o nulli e deducendo ove sono negativi ), si riporteranno questi dati
su un grafico per capire quante sono le possibili “combinazioni” di segno degli argomenti.
Per ciascuna delle combinazioni scriverò un sistema e la soluzione della disequazione sarà l’unione
delle soluzioni dei singoli sistemi.
Disequazioni irrazionali
Se l’indice è dispari, dopo aver isolato il radicale, eleverò entrambi i membri all’indice di radice in
modo da generare una disequazione razionale equivalente
Se l’indice è pari dovrò tener conto:
1. del campo di esistenza della radice
2. del segno del membro che non contiene la radice ( perché solo se i due membri sono non
negativi posso elevarli all’indice di radice, ottenendo una disequazione equivalente alla data)
3. se i due membri hanno già segno diverso, sono già in grado di stabilire se la disuguaglianza
è verificata.
Schemi da ricordare:
B  0

2
A  B
√A=B
B  0
A  0
o 

2
B  0
A  B
√A>B
√A<B
A  0

B  0
A  B2
