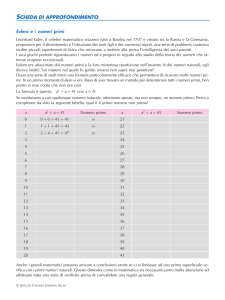
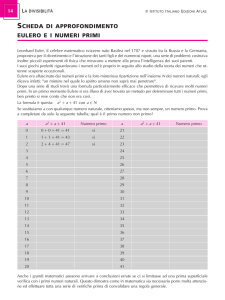
Le serie numeriche
Quasi tutti coloro che hanno avuto modo di dare un’occhiata ad un
testo matematico avanzato conoscono il significato del simbolo
8
a
i 1
i
che è una scrittura abbreviata per indicare la somma
a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8
Se il numero degli addendi è indeterminato, lo si indica con una
lettera, ad esempio n, e si scrive
n
a
i 1
i
Nei testi compare, però, anche una scrittura più misteriosa, che fa
pensare che gli addendi siano infiniti:
a
i 1
i
L’aritmetica non consente di effettuare questo tipo di operazione. Il
significato del simbolo, in effetti, è un altro, e proviene dal calcolo
infinitesimale, e più precisamente, dal concetto di limite. Si
definisce, infatti,
n
a lim a
i 1
i
n
i 1
i
dove la somma
n
a
i 1
i
prende il nome di n-esima somma parziale.
Il limite si dice somma della serie, e può anche non esistere, come
nel caso della serie
(1)
i 1
i 1
ossia
1 – 1 + 1 – 1 + 1 –….
In effetti le somme parziali valgono, alternatamente, 1 e 0. Una serie
siffatta si dice indeterminata.
I primi analisti, come Eulero e Jakob Bernoulli, avevano però
tutt’altra convinzione: non credendo possibile che una serie non
avesse somma, addussero vari argomenti a favore della tesi che la
somma fosse uguale ad ½.
Bernoulli non ebbe remore ad applicare la proprietà associativa della
somma alla serie
1 – 1 + 1 – 1 + 1 – ….
Chiamando S la somma di questa serie, sul cui valore i matematici
dell’epoca avevano pareri discordanti, Bernoulli osservò che da un
lato
S = (1–1) + (1–1) + (1–1) +….,
dall’altro
1 – S = 1 – (1–1) – (1–1) – … = 1 – 1 + 1 – 1 – …..
Ne dedusse che
S = 1 – S,
cioè S = 1/2. Ciò concordava perfettamente col fatto che le somme
parziali di indice pari sono uguali a 0, quelle di indice dispari sono
uguali a 1, e 1/2 è la media aritmetica dei due numeri.
Il matematico italiano Guido Grandi si sbizzarrì invece con la serie
1/(1+x) = 1 – x + x2 – x3 + …..
Questa espressione della funzione razionale fratta a primo membro
era stata ottenuta per i valori di x strettamente compresi fra –1 e 1.
Estendendo il principio di identità dei polinomi a serie infinite di
potenze, egli concluse che due funzioni algebriche coincidenti su di
un intervallo dovevano coincidere ovunque, e, con molta disinvoltura,
sostituì alla x i valori –2 e –1, trovando, rispettivamente:
– 1 = 1 + 2 + 4 + 8 +….
e
=1+1+1+1+…
Sostituendo valori maggiori di –1
la somma è invece sempre
maggiore di zero.
Eulero arrivò a giustificare questa contraddizione asserendo che
l’infinito, di cui ancora non era stata determinata la natura, potesse
essere visto come una sorta di separatore tra i numeri negativi e quelli
positivi. In effetti, sostituendo valori maggiori di –1 la somma della
serie è sempre maggiore di zero.
Bernoulli ed Eulero condividevano una certezza di fondo, che è il
tacito presupposto delle loro argomentazioni: le somme infinite, al
pari di quelle finite, sono sempre uguali ad un
numero,
eventualmente infinito. Eulero, in particolare, non ammetteva che
una serie potesse divergere, o essere indeterminata. Egli
le
considerava oggetti naturali, in quanto parti di problemi fisici, e
perciò credeva fermamente, come dice E. T. Bell, che esse non
potessero “fare alcun male”. Questa posizione è, curiosamente,
antitetica rispetto a quella di Zenone di Elea: la contraddittorietà del
paradosso di Achille e della tartaruga nasce proprio dalla
convinzione che la somma di infiniti addendi non possa essere uguale
ad una grandezza finita.
La somma di una serie può anche esistere, ma non essere uguale a
nessun numero reale. In tal caso è uguale a + oppure a –, come
negli esempi seguenti:
1 + 2 + 3 + 4 + 5 + …. = +
–
1 – 2 – 3 – 4 – 5 – …. = –
Una serie di questo tipo si chiama divergente. È divergente – pur se
questo fatto non è altrettanto evidente - anche la serie armonica,
studiata da Leibniz:
1
i
i 1
Infine, quando la somma di una serie esiste ed è pari ad un numero
reale, la serie si dice convergente:
(1)i 1
ln 2
i
i 1
1
1
i
i 1 2
(1) i 1
4
i 1 2i 1
Il secondo di questi esempi è ottenuto a partire dalla serie
logaritmica, che fu scoperta da Newton. Il terzo è una delle tante
serie notevoli nella cui somma compare
a Leibniz:
8
. Un’altra di queste è dovuta
1
1
1
1 3 5 7 9 11
Un’altra serie di questo tipo fu invece trovata da Eulero.
Leibniz e Cauchy introdussero importanti criteri di convergenza per
le serie.
Il matematico tedesco dell’Ottocento Leopold Kronecker, grande
avversario di Cantor e del concetto d’infinito, rifiutava l’uso delle
serie, giustificandosi così:
“Il concetto generale di serie infinita in sé, per esempio quello di serie di
potenze, è, a mio giudizio, ammissibile solo con la riserva che in ogni
caso particolare la regola aritmetica con la quale i termini sono dati
soddisfi condizioni che rendano possibile trattare le serie come se
fossero finite, in modo che non sia necessario, in senso stretto, andare
al di là della nozione di serie finita.”
In realtà alle serie non si applicano, in generale, le stesse regole valide
per le operazioni aritmetiche tra numeri. Estendere queste ultime alle
serie produce plateali contraddizioni, come mostrano certe
osservazioni di Eulero e Bernoulli. Ciò spinse il giovane matematico
norvegese Abel a dichiarare:
“Le serie divergenti sono un’invenzione del demonio, ed è una vergogna
basare su di esse una qualunque dimostrazione. Usandole, si può
giungere a qualsiasi conclusione si voglia, e per questo hanno prodotto
tante fallacie e paradossi…”