C. Ferone - Appunti delle lezioni
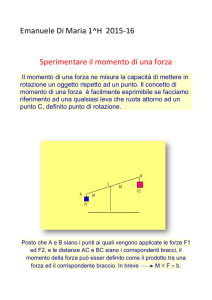
Forze e rotazioni: il momento di una forza
Un corpo rigido può compiere 2 tipi di moto:
Moto traslatorio, quando tutti i punti del corpo si muovono su traiettorie parallele
Moto rotatorio, quando tutti i punti del corpo descrivono traiettorie circolari con centri
appartenenti alla stessa retta, chiamata asse di rotazione.
Se l’asse di rotazione non rimane fermo nel tempo, il moto combinato del corpo è detto rototraslatorio.
Una porta è libera di ruotare intorno all’asse passante per i cardini, ma non di traslare. I cardini, infatti,
sono vincoli che mantengono fisso l’asse di rotazione.
Se pensiamo all’azione che dobbiamo compiere per aprire una porta, ci appare chiaro che oltre all’intensità,
alla direzione e al verso della forza che applichiamo, l’effetto prodotto dipende anche dal punto di
applicazione. Vediamo un altro esempio:
una maniglia è un corpo rigido vincolato ad uno dei suoi estremi che può ruotare intorno a tale vincolo
(ovvero il perno della maniglia): nessuno penserebbe di poter aprire una porta spingendo sul perno della
maniglia, infatti, a parità di forza applicata l’effetto è tanto maggiore quanto più la spinta è lontana dal
centro della rotazione.
La grandezza fisica che causa le rotazioni
Quindi, in presenza di una rotazione, intensità direzione e verso di una forza NON sono grandezze
esaurienti. Nelle rotazioni è importante il punto di applicazione (o la retta d’azione ) della forza e in
particolare la sua distanza dal centro di rotazione (nella figura precedente il centro di rotazione è il perno
della maglia indicato con il punto O).
La distanza tra fra il centro di rotazione O e la retta d’azione di una forza si chiama braccio della forza
rispetto al punto O.
1
C. Ferone - Appunti delle lezioni
Figura 2
Figura 1
Ricordiamo che si dice
distanza tra due punti
il segmento che ha per
estremi i due punti; si
dice distanza tra un
punto e una retta il
segmento
di
perpendicolare tra il
punto e la retta.
Nel caso delle rotazioni, dunque, intensità direzione e verso di una forza NON sono grandezze esaurienti, la
grandezza fisica che provoca le rotazioni deve tener conto anche del braccio della forza: il momento della
forza o momento torcente.
Quando apriamo una porta spingendo vicino allo spigolo, ad esempio, dobbiamo usare una forza molto
intensa, perché il braccio è corto e il momento è piccolo. Se invece ci spostiamo dallo spigolo e
aumentiamo il braccio aumenta anche il momento, e ci basta una forza inferiore per avere lo stesso effetto.
2
C. Ferone - Appunti delle lezioni
Come si calcola il braccio di una forza?
Nella Figura 1, il punto di applicazione della forza ha una distanza r = OA dal centro di rotazione, mentre la
distanza tra il centro di rotazione e la retta di azione della forza (braccio) è OH; per calcolare il braccio della
forza, conoscendo r e l’angolo che la direzione della forza forma con i raggio, si possono applicare le regole
della trigonometria.
dove
è una funzione dell’angolo che si calcola con la calcolatrice scientifica.
Nel caso della Figura 2, invece, la forza è applicata in direzione perpendicolare alla chiave inglese, il braccio
è dato dalla distanza tra il punto di applicazione della forza e il bullone; infatti il sen90 1.
Se invece la direzione della forza è parallela alla direzione della chiave, o della porta, o del raggio del disco
non si ottiene nessun effetto, cioè il corpo non ruota, infatti il braccio è nullo e anche il
.
Il seno e il coseno di un angolo
In un triangolo rettangolo, un cateto è uguale al prodotto
dell’ipotenusa per il coseno dell’angolo adiacente al cateto
stesso.
AC AB cos
cos
AC
AB
3
C. Ferone - Appunti delle lezioni
In un triangolo rettangolo, un cateto è uguale al prodotto dell’ipotenusa per il seno dell’angolo opposto al
cateto stesso.
AB è l’ipotenusa del
triangolo, BC è il cateto
opposto all’angolo α.
BC AB sen
sen
BC
AB
B
α
A
Il valore del seno e del coseno di un angolo ci viene fornito da apposite tabelle o da una calcolatrice
scientifica.
Stefania Mandolini – Le parole della Fisica – Zanichelli
Giuseppe Ruffo – Fisica, lezioni e problemi – Zanichelli
Caforio Ferilli – Fisica – Le Monnier
4
C