Rotazioni e curve ruotate. Scheda 1
1. Equazioni di una rotazione in tre casi particolari
Apri il file ‘Rotazioni_Scheda1a.ggb’: il piano trasparente Oxy ruota sul
piano fisso O’x’y’ attorno al punto O’, fino a che la semiretta O’x’ e la
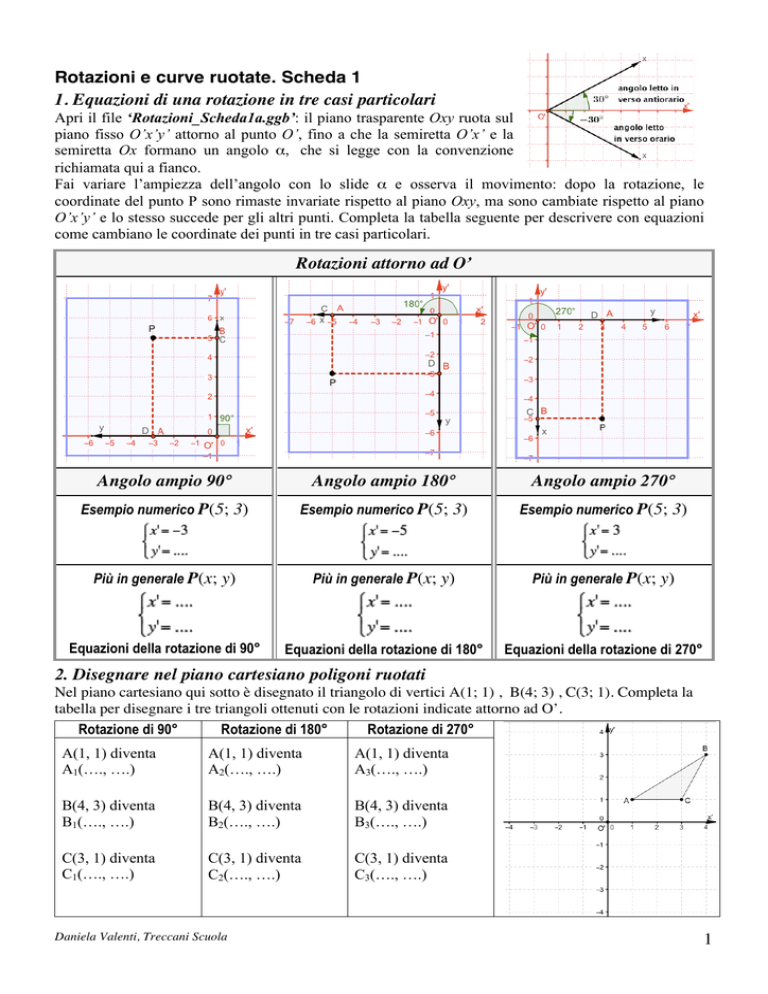
semiretta Ox formano un angolo α, che si legge con la convenzione
richiamata qui a fianco.
Fai variare l’ampiezza dell’angolo con lo slide α e osserva il movimento: dopo la rotazione, le
coordinate del punto P sono rimaste invariate rispetto al piano Oxy, ma sono cambiate rispetto al piano
O’x’y’ e lo stesso succede per gli altri punti. Completa la tabella seguente per descrivere con equazioni
come cambiano le coordinate dei punti in tre casi particolari.
Rotazioni attorno ad O’
Angolo ampio 90°
Angolo ampio 180°
Angolo ampio 270°
Esempio numerico P(5; 3)
Esempio numerico P(5; 3)
Esempio numerico P(5; 3)
Più in generale P(x; y)
Più in generale P(x; y)
Più in generale P(x; y)
Equazioni della rotazione di 90°
Equazioni della rotazione di 180°
Equazioni della rotazione di 270°
2. Disegnare nel piano cartesiano poligoni ruotati
Nel piano cartesiano qui sotto è disegnato il triangolo di vertici A(1; 1) , B(4; 3) , C(3; 1). Completa la
tabella per disegnare i tre triangoli ottenuti con le rotazioni indicate attorno ad O’.
Rotazione di 90°
Rotazione di 180°
Rotazione di 270°
A(1, 1) diventa
A1(…., ….)
A(1, 1) diventa
A2(…., ….)
A(1, 1) diventa
A3(…., ….)
B(4, 3) diventa
B1(…., ….)
B(4, 3) diventa
B2(…., ….)
B(4, 3) diventa
B3(…., ….)
C(3, 1) diventa
C1(…., ….)
C(3, 1) diventa
C2(…., ….)
C(3, 1) diventa
C3(…., ….)
Daniela Valenti, Treccani Scuola
1
3. Ruotare poligoni con un software di geometria dinamica
Apri il file ‘Rotazioni_Scheda1b.ggb’; troverai disegnato il triangolo
ABC e il punto O’ dati nell’attività 2. Procedi nel modo seguente:
• esplora il comando ‘Rotazioni’ per ruotare il triangolo ABC di 90°
attorno ad O’;
• usa ancora il comando ‘Rotazioni’ per ruotare ABC prima di 180° e poi di 270°attorno ad O’.
• modifica liberamente i vertici del triangolo per osservare le figure ottenute. In particolare che cosa
osservi se uno dei vertici del triangolo coincide con O’?
____________________________________________________________________________________
____________________________________________________________________________________
4. Equazioni di una rotazione attorno ad O’ di un angolo ampio α °
a. Osserva e completa la tabella seguente.
Nel piano Oxy
Nel piano O’x’y’, dopo una rotazione
attorno a O’ di un angolo ampio α
Nozioni da applicare
1. Definizione di seno e coseno di un
angolo con la circonferenza
goniometrica.
2. Formule di addizione del coseno e
del seno.
cos(β + α ) = cosβ ⋅ cosα − sinβ ⋅ sinα
sin(β + α ) = cosβ ⋅ sinα + sinβ ⋅ cosα
Alla fine dei calcoli si ottengono le
equazioni seguenti
P(x, y)
x = OP ⋅ cosβ
y = OP ⋅ ……
P(x’, y’)
x' = OP ⋅ cos(β + α )
y’ = OP ⋅ ………….
EQUAZIONI DELLA ROTAZIONE
b. Completa la tabella seguente per scrivere le equazioni ottenute nei casi particolari indicati
Angolo di rotazione
Calcoli
α = 45°
α = 135°
α = 60°
Daniela Valenti, Treccani Scuola
2












