Ottobre 2002

Corso di Laurea in Scienza dei Materiali
Laboratorio di Fisica III
Ottobre 2002
Seconda ESPERIENZA
Circuiti in corrente continua
A La legge di Ohm
Richiami teorici
Legge di Ohm (Tipler, 22.7):
V=RI
(1)
dove:
V = differenza di potenziale (unità di misura: volt, V)
I = intensità di corrente (unità di misura: ampere, A)
R = resistenza elettrica (unità di misura: ohm, )
Resistori collegati in serie. La resistenza equivalente vale (Tipler 22.19):
Req = R1 + R2 + R3 + ......
(2)
Resistori collegati in parallelo. La resistenza equivalente vale (Tipler 22.23):
1/Req = 1/R1 + 1/R2 + 1/R3 + ...
(3)
A1. Verifica della legge di Ohm
Verificate la legge di Ohm utilizzando almeno 2 diverse resistenze (R  100 ) e almeno 5
diversi valori di potenziale elettrico (4 V max). Disegnate lo schema elettrico del circuito,
indicando anche i collegamenti di voltmetro e amperometro, e riportate in un grafico i valori
ottenuti (caratteristica I-V, cioe’ I in funzione di V).
A2. Resistenze in serie
Collegando in serie delle opportune resistenze, realizzate una resistenza equivalente pari a circa
- 700  (per il gruppo 1)
- 800  (per il gruppo 2)
- 300  (per il gruppo 3)
- 400  (per il gruppo 4)
- 500  (per il gruppo 5)
- 600  (per il gruppo 6)
Applicate un potenziale elettrico (4V max) e misurate tutte le possibili correnti e le
differenze di potenziale ai capi delle resistenze (i valori vanno raccolti in una tabella con
notazioni chiare e leggibili); disegnate lo schema elettrico del circuito, indicando anche i
collegamenti di voltmetro e amperometro. (Suggerimento: annotate il fondo scala
dell’amperometro quando effettuate le misure)
A3. Resistenze in parallelo
Collegando in parallelo delle opportune resistenze, realizzate una resistenza equivalente pari
a circa:
- 600  (per il gruppo a)
- 500  (per il gruppo b)
1
- 400  (per il gruppo c)
- 300  (per il gruppo d)
- 200  (per il gruppo e)
- 100  (per il gruppo f)
Applicate un potenziale elettrico (4V max) e misurate tutte le possibili correnti e le
differenze di potenziale ai capi delle resistenze (i valori vanno raccolti in una tabella con
notazioni chiare e leggibili); disegnate lo schema elettrico del circuito, indicando anche i
collegamenti di voltmetro e amperometro. (Suggerimento: annotate il fondo scala
dell’amperometro quando effettuate le misure)
A4. Circuiti misti
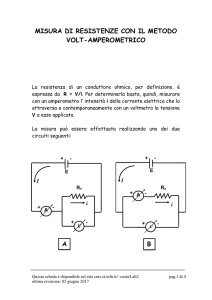
Realizzate il circuito rappresentato in figura scegliendo dei valori delle resistenze diversi fra
loro ma dello stesso ordine di grandezza (100-600 ).
Calcolate la resistenza equivalente, realizzate il circuito e verificate la correttezza del calcolo.
Inserite un potenziale di 5V fra i punti a e b e misurate le correnti nei diversi rami e le
differenze di potenziale ai capi delle resistenze.
(Suggerimento: annotate il fondo scala dell’amperometro quando effettuate le misure)
R1
a
R2
R1
R3
b
R4
R5
R6
A5. Voltmetro e amperometro
Determinate sensibilità e risoluzione del voltmetro e dell’amperometro del vostro multimetro
(se ci sono diverse scale, fatelo per ciascuna); valutate, per ogni scala, la resistenza interna
dell’amperometro realizzando il circuito seguente:
R
V = 1V
A
V
R = 0.3 M 
R = 1 K
R = 100 
R = 100 
R = 10 
per f.s. 200 A
per f.s. 2 mA
per f.s. 20 mA
per f.s. 200 mA
per f.s. 20 A
2
Spiegate l’andamento della resistenza interna dello strumento in funzione del valore di fondo
scala selezionato.
Valutate poi, per I fondo scala 2 V e 20 V, la resistenza interna del voltmetro, tramite il
circuito seguente:
V = 10 V per f.s. 20 V
V = 1.5 V per f.s. 2 V
R=
0.5 M 
A
V
In base ai valori ottenuti per la resistenza interna dell’amperometro e del voltmetro vedere se e’
necessario correggere i dati ottenuti ai punti A1-A4.
A6. Resistenza interna di sorgenti di differenza di potenziale
Un buon generatore di tensione deve avere una bassa resistenza interna per poter fornire sempre
la stessa tensione V indipendentemente dalla corrente I che sta erogando.
a-Resistenza interna dell’alimentatore di tensione. Impostate sull’alimentatore una differenza di
potenziale V non superiore a 1V leggendola direttamente sul voltmetro (è la tensione a
“circuito aperto”, anche se in realtà il circuito “si chiude” sull’alta resistenza interna del
voltmetro). Chiudete poi il circuito su una resistenza da 1 k e leggete il potenziale V
corrispondente. Ripetete la misura con resistenze da 100  e da 10 . Dalle tre misure
determinate, con relativo errore, il valore della resistenza interna Ri dell’alimentatore.
Disegnate lo schema elettrico del circuito, in cui Ri compaia esplicitamente.
b-Resistenza interna di una pila. Misurate la tensione che la pila eroga a “circuito aperto”.
Collegate la lampadina, dopo averne misurato la resistenza R, misurate nuovamente la
tensione e determinate la resistenza interna Ri della pila. Disegnate lo schema elettrico del
circuito, in cui Ri compaia esplicitamente.
A7. Accuratezza e precisione
Prendete 10 resistenze aventi lo stesso valore e tipo caratterizzato da un codice a 4 anelli,
misuratele con il multimetro e con un circuito apposito (di cui riporterete lo schema, V=2V
max), calcolate l’accuratezza e la precisione con cui sono state fabbricate.
Ripetete la misura con 10 resistenze aventi un valore simile e tipo caratterizzato da un codice
a 6 anelli.
B Leggi di Kirchoff
Richiami teorici (v. Tipler cap. 23.1)
Prima legge: in ogni nodo di un circuito in cui la corrente può dividersi, la somma delle intensità
delle correnti che entrano nel nodo è uguale alla somma delle intensità delle correnti che escono.
Seconda legge: se si percorre una maglia di un circuito in un verso arbitrario e prefissato, la somma
algebrica delle variazioni di potenziale è nulla.
3
B1. Nodi e maglie
Realizzate il circuito rappresentato in figura scegliendo dei valori diversi fra loro ma dello
stesso ordine di grandezza per le resistenze e per le differenze di potenziale. Calcolate le
correnti nei tre rami del circuito e le differenze di potenziale ai capi delle resistenze, poi
misuratele e verificate la correttezza dei calcoli.
R2
R1
V1
V2
R3
B2. Il potenziometro
Usando il potenziometro con fondo corsa di 1 k, realizzare il circuito in figura con V0 = 6 V,
V=4.5 V. Aggiustate il cursore del potenziometro in modo che Vc = Vd (cioè la corrente nel ramo cd sia nulla).
b
V
c
Ri
A
R
d
a
e
Vo
Giustificate il risultato servendovi dell’analisi di maglia.
C Resistività, dipendenza dalla temperatura, potenza e intensità luminosai
Richiami teorici
La resistività  è legata alla resistenza elettrica dall’equazione (Tipler 22.8):
=RA/l
(4)
dove l è la lunghezza e A è la sezione del conduttore.
4
Dipendenza della resistività dalla temperatura Per temperature prossime alla temperatura ambiente,
la resistività dipende linearmente dalla temperatura secondo la legge (Tipler 22.11):
 = 293 [1+ (T - 293)]
da cui, trascurando le dilatazioni termiche:
R = R293 [1+ (T - 293)]
(5)
(5’)
dove T è la temperatura misurata in kelvin, 293 è la resistività a 293 K e  è il “coefficiente di
temperatura della resistività” (per i buoni conduttori come il rame vale 3,810-3 K-1, per il
tungsteno vale 4,510-3 K-1).
Potenza dissipata e intensità luminosa La potenza P dissipata in un tratto di circuito in cui circola
una corrente I e ai cui capi c’è una caduta di potenziale I vale (Tipler 22.12):
P=IV
(6)
La potenza viene prevalentemente dissipata sotto forma di calore (effetto Joule). Ad alte
temperature diventa dominante la dissipazione sotto forma di radiazione. La potenza dissipata sotto
questa forma è legata alla temperatura assoluta T dalla legge di Stefan-Boltzmann (Tipler 16.3):
P = S A T4
(7)
dove S è la cosidetta “costante di Stefan-Boltzmann” e A è l’area della superficie emettitrice.
C1. Misure di resistività
Misurate la resistività a temperatura ambiente del filo di rame argentato della bobina che
trovate sul tavolo (la lunghezza del filo è di 4m, il diametro va misurato da voi).
Ripetete la misura a 3 temperature più alte (usando il becker con acqua calda) e alla
temperatura dell’azoto liquido. Riportate i dati in un grafico, verificate che la dipendenza
dalla temperatura di  sia lineare come atteso dall’eq. (5) se  è costante, e determinate
il coefficiente  eseguendo una regressione lineare.
C2. Resistenza e legge di Stefan-Boltzmann
Collegate la lampadina che trovate sul tavolo di lavoro in modo da poter misurare corrente e
differenza di potenziale e costruite la caratteristica I-V badando ovviamente di non superare il
massimo potenziale di alimentazione (4.5 V).
Riportate la caratteristica in un grafico e verificate graficamente la deviazione dalla legge
di proporzionalità diretta fra tensione e corrente attesa per resistenza costante.
Per ogni valore di V calcolate il valore di R e, assumendo che l’eq. (5’) sia valida in tutto
l’intervallo di temperatura, calcolate il valore di T per ogni valore di V e riportate in un
grafico T in funzione di V. In particolare calcolate il valore di T al potenziale di
funzionamento consigliato e al potenziale a cui la luce emessa comincia ad essere
apprezzabile.
Per ogni valore di V calcolate il valore della potenza dissipata P(eq. 6), riportate in un
grafico P in funzione di T4 e verificate se la potenza dissipata segue la legge di StefanBoltzmann (eq. (7), valida nel caso in cui tutta l’energia sia dissipata in forma di energia
radiante).
5
D Conduttori non ohmici
Richiami teorici
La dipendenza dalla temperatura della resistività fa sì che anche un buon conduttore “ohmico”
mostri apparenti deviazioni dalla legge di Ohm (cioè la corrente non varia proporzionalmente alla
tensione applicata): tali deviazioni però scompaiono se si tiene il conduttore a temperatura costante.
Esistono invece dei dispositivi che si discostano dalla legge di Ohm anche se la temperatura viene
mantenuta rigorosamente costante: un dispositivo di questo tipo è il “diodo”, che è una giunzione di
due pezzi di materiale “semiconduttore” trattati (“drogati”) diversamente: nel drogaggio un lato
della giunzione (lato n) viene arricchito di elettroni di conduzione, mentre l’altro lato (lato p) viene
arricchito di posti vuoti ( detti “buche” oppure “holes”) nella banda di valenza (per approfondimenti
v. Tipler 39.7).
Il LED Il diverso tipo di drogaggio e le caratteristiche intrinseche del semiconduttore (presenza nel
semiconduttore di una banda di energie “proibite” agli elettroni –“energy gap, Egap ”–) fanno sì che,
applicando alla giunzione una differenza di potenziale V tale che il lato p sia a potenziale più alto
del lato n (polarizzazione “diretta”) gli elettroni riescono a passare molto più facilmente dal lato n
al lato p della giunzione e contemporaneamente le buche a passare, in senso inverso, dal lato p al
lato n. Le due correnti si sommano, perché elettroni e buche hanno segno opposto di carica elettrica
ma si muovono anche in direzione opposta, per cui la corrente totale cresce rapidamente con
l’aumento di V. La relazione fra tensione e corrente non è lineare ma esponenziale:
I = I0 [exp (qeV / KB T) – 1]
(8)
dove  è una costante numerica che dipende dal diodo e vale circa 1.5, kB è la costante di
Boltzmann (pari a 8,510-5 eV K-1) e qe è la carica dell’elettrone. Il potenziale V è inteso positivo
per polarizzazione diretta. Dato che Io è molto piccolo, si inizia ad avere correnti apprezzabili, con i
diodi che userete, per tensioni superiori a 1,5 V.
Applicando invece alla giunzione una differenza di potenziale V tale che il lato p sia a potenziale
più basso del lato n, cioè V sia negativo (polarizzazione “inversa”), il passaggio degli elettroni dal
lato n al lato p della giunzione e quello delle buche in senso inverso sono ulteriormente ridotti per
cui, come si vede dalla (8), la corrente è negativa ma così piccola da non essere rivelabile con un
normale amperometro.
Nella figura sono esemplificati due semplici circuiti, in polarizzazione diretta e inversa. Come si
vede, negli schemi dei circuiti elettrici il diodo viene indicato con un simbolo formato da una barra
e un triangolo, con il lato p della giunzione associato al triangolo.
I diodi che userete sono dei LED (Light Emitting Diode). In questi diodi, raggiunti valori di
corrente sufficientemente alti, per cui il numero di elettroni di conduzione nel lato p della
giunzione è elevato, diventa molto probabile la ricombinazione fra elettroni e buche:
l’energia rilasciata nella ricombinazione, che è dell’ordine di Egap , viene emessa sotto forma
di fotoni di energia Ef prossima al valore di Egap . L’energia del fotone è legata alla
lunghezza d’onda  della luce emessa dalla relazione di Einstein:
Ef =hc/ 
(9)
8
dove c è la velocità della luce nel vuoto (c=310 m/s) e h è la costante di Planck (costante
fondamentale della meccanica quantistica, pari a 4,1108eV s): conoscendo perciò il valore della
lunghezza d’onda a cui il diodo emette è possibile risalire, attraverso la (9) al valore di Egap.
Con i LED che userete, è possibile risalire a Egap anche in un altro modo. Infatti, quando qeV
diventa maggiore di Egap , la corrente tende a crescere, al crescere di V, più lentamente di
quanto previsto dalla (8), finché, ad alte correnti, l’andamento torna a essere circa lineare
6
come nella legge di Ohm. Estrapolando all’indietro l’andamento lineare fino a corrente nulla,
si trova che l’intercetta Vo corrispondente è pari a Egap / qe:
Egap = qe Vo
(10)
Polarizzazione diretta
Polarizzazione inversa
R
V
V
Cella fotovoltaica
La cella fotovoltaica è basata su un tipo particolare di diodo in cui l’esposizione alla luce
causa, con molta efficienza, il passaggio di elettroni dalla banda di valenza a quella di
conduzione.
a
voltmetro Ri
o
amperometro
direzione
della
corrente
lato p
direzione
del flusso
di elettroni
lato n
Rcella
b
Il lato che viene esposto alla luce è il lato p della giunzione, gli elettroni vengono eccitati
dalla luce nella banda di conduzione e di qui tendono a migrare verso il lato n della
giunzione: si crea quindi un flusso di elettroni dal lato p al lato n e quindi una corrente
elettrica dal lato n verso il lato p. Questa direzione della corrente corrisponde alla situazione
di “polarizzazione inversa” discussa sopra: la cella fotovoltaica funziona quindi in condizioni
di polarizzazione inversa, in cui tuttavia la corrente non è piccolissima, perché è favorita
dalla eccitazione dovuta alla luce. La corrente infatti è proporzionale all’illuminamento.
7
I parametri importanti di una cella fotovoltaica sono la “corrente a circuito chiuso” (Icc) e la
“tensione a circuito aperto” (Vca ).
La prima si misura inserendo fra i capi “a” e “b” della cella un amperometro: poiché
l’amperometro ha una resistenza interna Ri piccola, la corrente che circola nel circuito è
determinata dal potenziale Vo effettivamente generato dal passaggio degli elettroni nella cella
diviso per la resistenza interna Rcella della cella:
Icc = Vo / Rcella
(11)
La differenza di potenziale a circuito aperto si misura inserendo fra i capi “a” e “b” della cella un
voltmetro: poiché il voltmetro ha una resistenza interna Ri molto grande, la corrente che circola nel
circuito è piccolissima e quindi la caduta di potenziale sulla resistenza interna della cella è
trascurabile e si può assumere che
Vca  Vo
(12)
Misurando Vca e Icc , si può quindi risalire ai valori di Rcella e di Vo .
D1. Caratteristica I-V del diodo emettitore di luce (LED)
Collegate il LED rosso all’alimentatore inserendo per protezione una resistenza di circa
100. Disegnate lo schema del circuito e misurate la caratteristica I-V, badando a non
superare i 2.5 V nella caduta di potenziale ai capi del LED, e riportate i dati in un grafico.
a-Individuate la parte lineare della caratteristica ed estrapolate i dati al valore di I=0,
determinando il valore Vo dell’intercetta. Supponendo che qe Vo rappresenti una buona
stima di Egap (eq. 10) e quindi dell’energia Ef del fotone emesso, determinate il valore
aspettato per la lunghezza d’onda  della luce emessa in base alla relazione di Einstein
(eq. 9). Ripetete le misure per il LED giallo e verde. I valori aspettati per  sono 680 nm,
600 nm, 580 nm rispettivamente per i LED rosso, giallo e verde.
b-Riportate nuovamente i dati in un grafico, usando per la corrente I una scala logaritmica.
Individuate la parte che segue bene la legge esponenziale di eq. 8 (il termine –1 che
compare nell’equazione è completamente trascurabile alle correnti misurabili col vostro
amperometro) e determinate il valore della costante .
D2. Caratteristica I-V di una cella fotovoltaica
Esponete la cella fotovoltaica alla luce della lampada. Misurate la differenza di potenziale a
circuito aperto Vca, la corrente di corto circuito Icc e determinate la resistenza interna della
cella, Rcella. Collegate alla cella una resistenza di carico R, misurate la corrente I, la caduta di
potenziale V e calcolate la potenza estratta W. Ripetete la misura per diversi valori di R e
trovate il valore che rende massima la potenza. Confrontate tale valore con quello della
resistenza interna della cella.
Riportate in un grafico I, V e W in funzione di R.
Ripetete l’intera misura per una diversa intensità di illuminazione.
E Condensatori
Richiami teorici
Condensatori collegati in parallelo : la capacità equivalente è la somma delle capacità dei singoli
condensatori (Tipler 21.21):
Ceq = C1 + C2 + …..
(13)
Condensatori collegati in serie : l’inverso della capacità equivalente è la somma degli inversi delle
capacità dei singoli condensatori (Tipler 21.25):
8
1/Ceq = 1/C1 + 1/C2 + …..
(14)
Capacità di un condensatore a facce piane e parallele (Tipler 21.11):
C = r o A / d
(15)
-12
dove o = 9 10 F/m, r è la costante dielettrica relativa, A è l’area dell’armatura e d la loro
distanza.
E1. Collegate in serie tre condensatori aventi valori di capacità diversi ma dello stesso ordine
di grandezza, misurate la capacità equivalente e confrontatela con il valore calcolato.
Collegate poi i condensatori in parallelo ed eseguite lo stesso tipo di misura e di calcolo.
E2. Misurate la capacità dei tre LED usati nell’esperimento D1 in assenza di potenziale
applicato dall’esterno. La giunzione di un LED si comporta come un condensatore a facce
piane avente area pari all’area della giunzione e distanza fra le armature pari allo spessore del
cosiddetto “strato di svuotamento” che si crea fra i due lati della giunzione (è chiamato in
questo modo perché in esso non esistono né elettroni di conduzione liberi di muoversi né
buche libere: si comporta quindi come il dielettrico che si mette fra le armature del
condensatore). Dal valore della capacità, calcolate lo spessore dello strato di svuotamento,
supponendo che l’area della giunzione sia di circa 0.1 mm2 e che la costante dielettrica
relativa r del semiconduttore sia circa 10.
F Carica e scarica del condensatore.
Richiami teorici
Durante la scarica o la carica del condensatore, la corrente che circola nel circuito segue un
andamento esponenziale in funzione del tempo (v. Tipler eq. 23.20 e 23.27):
I = I0 e -t/
(16)
dove il tempo caratteristico  è pari al prodotto della resistenza R per la capacità C del
circuito,  = R C. Anziché misurare I, che sarebbe piccolissimo, misurerete la caduta di
potenziale VR ai capi della resistenza, che è proporzionale a I .
F1. Collegate all’alimentatore un condensatore da 10 F e, in serie, una resistenza da 1 M
circa. Costruite la curva di carica prelevando la caduta di potenziale ai capi della resistenza a
intervalli di tempo di 2 secondi. Riportate in un grafico il potenziale in funzione del tempo;
determinate –possibilmente con una regressione lineare mediante una opportuna scelta della
funzione da utilizzare come variabile dipendente – il valore della costante di tempo  e
confrontatela con il valore aspettato di  , dato dal prodotto RC.
Calcolate, per differenza, il potenziale ai capi del condensatore e riportatelo in un grafico in
funzione del tempo.
Ripetete la misura e l’elaborazione dei dati per la scarica del condensatore.
Disegnate per ciascuna misura lo schema del circuito utilizzato.
Discutete se è trascurabile la resistenza interna del voltmetro. Se non lo è, valutate la correzione che
andrebbe apportata al valore aspettato di  . Ridisegnate il circuito includendo anche la resistenza
interna del voltmetro.
9