Sanità

4^ Esercitazione CLES
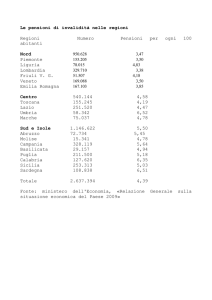
Sanità – Pensioni
Esercizio 1 - Sanità
Considerate una comunità composta da individui con differenti probabilità di ammalarsi:


individui di tipo H, che rappresentano il 55% della popolazione, con una probabilità di ammalarsi pari al
70%;
individui di tipo L, che rappresentano il 45% della popolazione, con una probabilità di ammalarsi pari al
30%.
In caso di malattia il danno è pari a 100 per entrambi i gruppi.
In un mercato perfettamente concorrenziale e in assenza di costi di amministrazione, si determinino i premi
richiesti ai due tipi di individui per unità di materia assicurata e si dica se gli individui scelgono di acquistare
una copertura completa o parziale nel caso in cui:
a) l’informazione sia perfetta;
b) l'impresa assicuratrice non riesca a discriminare tra i due tipi di individui (asimmetria informativa) ed
offra ad entrambi i gruppi lo stesso contratto con un premio tale da rendere i profitti complessivi nulli (in
valore atteso). Si discutano brevemente i problemi che sorgono in questa situazione.
Soluzione
a) In un mercato perfettamente concorrenziale, deve valere la condizione di profitti attesi nulli: E(P)=0. E’
possibile mostrare che, con informazione perfetta (simmetrica), tale condizione implica che l’impresa
richieda ad entrambi i tipi di individui il pagamento di premi attuarialmente equi, cioè pari alla
probabilità dell’evento negativo. Indicando con N la numerosità della popolazione, con q il livello di
copertura scelto, con pi e con πi rispettivamente il premio pagato e la probabilità di ammalarsi per il tipo
i-esimo:
E(P)= 0,55 N pH q – 0,55 N πH q + 0,45 N pL q – 0,45N πL q = 0
da cui segue:
pH = πH = 0,7 per gli individui H e pL = πL = 0,3 per gli individui L.
In questo caso entrambi i gruppi chiedono copertura completa:
q = d = 100.
b) Se l'informazione è asimmetrica, l'assicuratore non discrimina tra agenti H e L e può essere indotto ad
offrire a tutti un unico contratto. Se la popolazione è sufficientemente numerosa e i rischi indipendenti, il
profitto atteso può essere scritto come:
E(P)= Npq – 0,55 N πH q – 0,45N πL q
In questo caso, assumendo che tutti gli individui accettino di sottoscrivere il contratto, la condizione di
profitti attesi nulli impone la richiesta di un premio pari alla probabilità media di malattia per l’intera
popolazione. Pertanto, E(P)=0 se e solo se:
p = 0,55 πH + 0,45 πL = 0,55 x 0,7 + 0,45 x 0,3 = 0,52.
I problemi derivano dal fatto che questo premio è superiore alla probabilità di ammalarsi per gli
individui di tipo L, i quali quindi non si assicureranno e usciranno dal mercato. Questo implica che la
qualità media degli assicurati diminuisce (fenomeno di selezione avversa), le imprese aumentano i premi
(per evitare profitti negativi), rimangono solo individui di tipo H e il premio aumenta fino a raggiungere
il valore massimo per gli individui ad alto rischio (nel nostro caso 0,7).
Esercizio 2 - Sanità
Il paese X decide di iniziare a fornire i farmaci gratuitamente. La funzione di domanda della collettività
stimata è la seguente:
q = 10000 – 10 p
dove q indica la quantità di farmaci richiesta e p il prezzo medio di tali farmaci.
Il prezzo medio per farmaco è di 300.
a) Definire il concetto di azzardo morale. Come si applica alla situazione del paese X?
b) Calcolare la perdita di bilancio rispetto alla situazione di perfetta informazione nel caso si pongano
problemi di azzardo morale.
c) In seguito ad un’attenta analisi, il governo di X si rende conto di non avere alcuna possibilità di
controllare il comportamento dei consumatori. Allo stesso tempo, però, per ragioni di finanza pubblica,
la spesa farmaceutica a carico dello stato non può in alcun caso eccedere il tetto di 1.800.000. Quali
manovre potrebbe attuare al fine di raggiungere questo livello di consumo farmaceutico?
Soluzione
a) AZZARDO MORALE: poiché l’impresa di assicurazione non è in grado di controllare il comportamento
degli assicurati dopo la stipula del contratto, l’individuo può domandare più cure di quanto strettamente
necessario, oppure può influenzare la probabilità che si verifichi l’evento negativo.
Nel nostro caso la quantità di farmaci venduta in corrispondenza di un prezzo pari a 300 (quantità con
perfetta informazione) è:
q PI = 10000 – 10 p = 10000 – 10 (300) = 7.000.
Il problema di azzardo morale nasce dal fatto che nel paese X gli individui ricevono farmaci
gratuitamente (quindi, per i cittadini-consumatori, p = 0), mentre il prezzo effettivo è pagato dal governo.
La quantità domandata (quantità con moral hazard) sarà dunque pari a:
q MH = 10000 – 10 p = 10.000.
I pazienti fanno quindi ricorso a cure addizionali rispetto a quelle cui farebbero ricorso qualora non esistesse
un sistema farmaceutico pubblico e gratuito.
b) Nell’ipotesi di azzardo morale, la spesa farmaceutica per il governo del paese X è:
q MH  p = 10000 x (300) = 3.000.000.
Nell’ipotesi di perfetta informazione si ha invece che:
q PI  p = 7000 x (300) = 2.100.000.
La perdita di bilancio dovuta all’asimmetria informativa è pertanto di 900.000.
c) Al fine di disincentivare l’eccessivo consumo di farmaci, è prassi utilizzare sistemi di compartecipazione
al finanziamento delle spese sanitarie: il paese X introduce a tal fine i ticket.
Pertanto, il prezzo medio per farmaco, p = 300, è coperto per un ammontare fisso (x) dal cittadinoconsumatore, e per il restante ammontare (300 - x) dallo Stato.
Dal momento che il cittadino-consumatore paga x per ogni unità di farmaco, la domanda di farmaci sarà:
q = 10.000 - 10x.
Pertanto, la spesa farmaceutica complessiva a carico dello Stato è:
(10.000 – 10x) (300 – x)
Dato il vincolo di spesa che lo Stato deve rispettare, otteniamo:
(10.000 – 10x) (300 – x) = 1.800.000
che equivale a:
10x2 – 13.000x + 1.200.000 = 0
 x = 100*.
Il governo del paese X dovrebbe, pertanto, richiedere ai cittadini-consumatori di coprire 1/3 del prezzo
medio dei farmaci.
*La quota di compartecipazione al prezzo x pagata dal consumatore non può eccedere il prezzo
complessivo del bene acquistato. Per tale ragione la radice x = 1220 non può essere la soluzione del
quesito posto.
Esercizio 3 - Sanità
Si consideri una collettività costituita da 2 individui, uno giovane e uno anziano. Entrambi hanno un reddito
pari a 30 e subiscono un danno pari a 100 in caso di malattia. Il giovane ha una probabilità G=0,2 di
ammalarsi, mentre l’anziano ha una probabilità A=0,7. I due individui sono perfettamente distinguibili dalle
compagnie assicurative.
a) Si determini il grado di copertura ottimale q* scelto da ciascun individuo in corrispondenza di un
premio attuarialmente equo.
b) Si calcoli il premio complessivo che ciascun individuo dovrebbe pagare per ottenere la copertura
desiderata.
c) Quale problema si pone? Commentate, alla luce di questo risultato, l’intervento pubblico
nell’organizzazione, prevalentemente privata, del sistema sanitario degli Stati Uniti.
Soluzione
a) Siano per i = G, A:
pi = premio unitario
qi = risarcimento
d = danno
w i1 = reddito se non si verifica l’evento negativo = w – piqi
w i2 = reddito se si verifica l’evento negativo = w – d – piqi + qi
Ogni individuo massimizzerà la sua utilità attesa quindi il problema da risolvere è:
Max
E[U ( wi )]   U ( wi 2 )  (1   )U ( wi1 )   U ( wi  d  q i  p i q i )  (1   )U ( wi  p i q i )
i
q
La condizione del primo ordine è:
i
i
E[U ( wi )]
i U ( w 2 )
i
i U ( w 1 )


(1

p
)

(1


)
( p i )  0
qi
wi 2
wi1
Ovvero:
 i U '( wi 2 )
pi

1   i U '( wi1 ) 1  pi
Poiché i premi sono attuariamente equi si avrà che pi   i con i = G, A. Quindi la condizione del primo
ordine sarà:
U '( wi1 )  U '( wi 2 )
Il che si verifica solo quando wi1  wi 2 da cui risulta qi  d con i = G, A.
La copertura ottimale richiesta da individui avversi al rischio in corrispondenza di premi attuarialmente
equi è quindi completa:
qi* = d = 100
b) Il premio complessivo per il giovane sarà:
pGq = 0,2 × 100 = 20
e per l’anziano:
pAq = 0,7 × 100 = 70.
c) L’esercizio mostra come un sistema sanitario di natura privata “fallisca” nel garantire una copertura
sanitaria alla cittadinanza nel suo complesso, dal momento che possono esistere persone bisognose di
cure, ma non in grado di pagare il premio previsto per vincoli di reddito (l’anziano ha un reddito di 30,
ma dovrebbe pagare un premio di 70!). Si rende pertanto necessario l’intervento dello Stato per garantire
la copertura a taluni segmenti della popolazione. Questo è, ad esempio, ciò che succede negli USA dove
è presente un sistema di assicurazioni sanitarie private ma lo Stato interviene a sostegno degli anziani e
dei poveri mediante i programmi denominati MEDICARE e MEDICAID.
Esercizio 4 - Sanità
La popolazione del paese X è composta per il 50% da individui (tipo A) che hanno una probabilità di
ammalarsi pari al 20% e per il restante 50% da individui (tipo B) che hanno una probabilità di ammalarsi pari
al 70%. Sia gli individui di tipo A che gli individui di tipo B guadagnano, in condizioni normali, un reddito
di 1000 che si riduce, in caso di malattia, a 200. Gli individui hanno la possibilità di acquistare
un’assicurazione.
a)
Si ipotizzi che la compagnia assicuratrice sia in grado di distinguere perfettamente i due tipi A e B e
offra loro l’assicurazione dietro il pagamento di un premio attuarialmente equo. Si determini
(distinguendo, se necessario, tra gli individui):
1. il premio unitario;
2. la quantità di assicurazione acquistata e il premio complessivo;
3. il reddito degli individui al netto dei premi assicurativi;
4. il profitto atteso dell’impresa assicuratrice.
b)
Si ipotizzi ora che l’impresa non sia in grado di distinguere i due tipi di individui e che offra a tutti
un unico contratto con un premio che le consenta di conseguire profitti attesi nulli.
5. A quanto ammonterà il premio unitario che l’impresa deciderà di applicare?
6. Chi beneficerà dell’assenza di perfetta informazione?
7. Si modificheranno le scelte assicurative delle due tipologie di individui?
8. Se sì, con quali conseguenze per il mercato assicurativo?
Soluzione
a)
Informazione perfetta
1. In caso di informazione perfetta il premio unitario attuarialmente equo per i due tipi di individui
corrisponde alle rispettive probabilità che si verifichi l’evento negativo:
pA = πA = 0,2
pB = πB = 0,7
2. In presenza di premi attuarialmente equi gli individui sceglieranno di acquistare una quantità di
assicurazione che consenta loro di avere copertura completa (q=d):
qA = qB = q = d = 1000 – 200 = 800
Il premio complessivo per A e per B sarà quindi rispettivamente:
pA q = 0,2 x 800 = 160
pB q = 0,7 x 800 = 560
3. Quando gli individui acquistano copertura completa (q=d), il reddito degli individui al netto dei
premi assicurativi è costante nei due stati del mondo (salute e malattia) ed è quindi pari a:
YA = 1000 – 0,2 x q = 1000 - 160 = 840
YB = 1000 – 0,7 x q =1000 - 560 = 440
4. Il profitto atteso dell’impresa assicuratrice sarà (la popolazione è equamente distribuita tra
individui di tipo A e di tipo B):
E(P) =0,5N (pA q - πA q + pB q – πB q) = 0
b)
Asimmetria informativa
5. In caso di asimmetria informativa l’impresa assicuratrice non discrimina tra gli individui a basso e
ad alto rischio e può essere indotta ad offrire a tutti un unico contratto. Il premio unitario che verrà
proposto dall’impresa (che rende i profitti complessivi nulli in valore atteso) è pari alla probabilità
media di malattia per l’intera popolazione.
p= 0,2 x 0,5 + 0,7 x 0,5 = 0,1 + 0,35 = 0,45
6. Le persone che hanno probabilità maggiore di ammalarsi (tipo B) possono sfruttare a loro
vantaggio l’assenza di perfetta informazione che pesa sull’impresa assicurativa. Infatti si
troveranno a pagare un premio unitario (0,45) inferiore alla loro probabilità di malattia (0,7).
7. Le scelte assicurative per i due gruppi di individui si modificheranno: infatti gli individui a più
basso rischio (tipo A) decideranno di non assicurarsi perché il premio medio (0,45) risulterà più
elevato rispetto alla probabilità che si verifichi l’evento negativo (0,2) (selezione avversa).
8. La fuoriuscita dal mercato assicurativo degli individui a basso rischio comporterebbe una
riduzione della qualità media degli assicurati con la conseguenza che le imprese assicuratrici
sarebbero costrette ad aumentare i premi per evitare perdite, peggiorando ulteriormente il
problema della selezione avversa. Il premio unitario salirà fino al valore massimo per gli individui
di tipo B (0,7), ormai i soli presenti sul mercato.
Esercizio 5 - Pensioni
a) Qual è la differenza tra sistema pensionistico a ripartizione con metodo contributivo e sistema
pensionistico a capitalizzazione?
b) Si supponga che ciascuna generazione viva per due periodi: nel primo lavora e versa contributi
previdenziali, nel secondo cessa di lavorare e percepisce una pensione. Ipotizzando che nel paese il
monte salari Wt del primo periodo sia pari a 100, che l’aliquota contributiva α sia del 30%, il tasso di
crescita della produttività m del 2% e quello dell’occupazione n dell’1% e il tasso di interesse corrente i
sia dell’1%, si calcolino:
- i contributi versati in t (Ct)
- il monte pensioni in t+1 (Pt+1)
- il rendimento ottenuto dalla generazione che lavora e versa i contributi in t
a seconda che venga applicato un sistema pensionistico a ripartizione o a capitalizzazione.
Soluzione
a) In un sistema a ripartizione i contributi riscossi in ogni periodo sono destinati al finanziamento delle
prestazioni pensionistiche erogate nello stesso periodo. Il metodo contributivo prevede in particolare che
la pensione annuale sia determinata uguagliando il montante contributivo individuale (MC) al valore
attuale delle pensioni future (VA), dove il montante contributivo è ottenuto capitalizzando i contributi
versati ad un tasso prefissato r. Nel sistema pensionistico a capitalizzazione i contributi che ogni
lavoratore versa nel periodo di attività sono investiti sul mercato dei capitali (al tasso di interesse di
mercato i) e destinati a finanziare la pensione del lavoratore stesso. Il calcolo delle prestazioni
pensionistiche è analogo a quello del sistema a ripartizione con metodo contributivo, con la differenza
che il MC è determinato sulla base del rendimento effettivamente ottenuto sui contributi investiti sul
mercato dei capitali.
b) Monte salari Wt = 100
α = 0.3
m = 0.02
n = 0.01
i = 0.01
In un sistema pensionistico a ripartizione si avrà che:
Contributi versati in t = Ct = α Wt = 0.3*100 = 30
Monte pensioni in t+1 = Pt+1 = Ct+1 = α Wt+1 = α Wt (1+m)(1+n) = 0.3*100(1.02)(1.01) = 30.906
Rendimento implicito ottenuto dalla generazione che lavora e versa i contributi nell’anno t:
(Pt+1 / Ct)-1 = (Pt+1/α Wt)-1 ≈ m + n = 0.02 + 0.01 = 3%
In un sistema pensionistico a capitalizzazione si avrà che:
Contributi versati in t = Ct = α Wt = 30
Monte pensioni in t+1 è pari ai contributi versati nel periodo precedente, capitalizzati al tasso di interesse
corrente i:
Pt+1 = Ct (1 + i) = α Wt (1 + i) = 30 (1.01) = 30.3
Rendimento ottenuto dalla generazione che lavora e versa i contributi nell’anno t è pari al tasso di
interesse corrente i = 0.01 = 1%.
Esercizio 6 - Pensioni
Un individuo ha lavorato per 35 anni percependo per i primi 10 anni uno stipendio annuo di 30, nei
successivi 20 di 40 e negli ultimi 5 di 50. Si calcolino la pensione cui ha diritto il lavoratore ed il tasso di
sostituzione nei casi seguenti:
a) metodo di calcolo retributivo:
a. coefficiente di rendimento 2%, retribuzione pensionabile pari alla media delle retribuzioni
dell’intera vita lavorativa, nessuna rivalutazione delle retribuzioni;
b. coefficiente di rendimento 2%, retribuzione pensionabile pari alla media delle retribuzioni
degli ultimi cinque anni, nessuna rivalutazione delle retribuzioni;
b) metodo di calcolo contributivo: aliquota contributiva del 20%, nessuna rivalutazione dei contributi, tasso
di sconto del valore futuro delle pensioni pari a 0 e speranza di vita del lavoratore al momento del
pensionamento di 20 anni.
Soluzione
Nel caso in esame si ha:
numero di anni di contribuzione: L = 35 anni;
salario primi dieci anni: w1 = 30;
salario successivi vent’anni: w2 = 40;
salario ultimi cinque anni: w3 = 50;
coefficiente di rendimento:  = 2%.
1. Metodo retributivo
Ricordando che le formule per calcolare la pensione e il tasso di sostituzione sono rispettivamente:
P =  RP L;
s = P / RL;
dove RP = retribuzione pensionabile e RL = ultima retribuzione percepita, avremo:
a) P = 2% x {[(30 x 10 + 40 x 20 + 50 x 5) / 35] x 35} = 27
s = P / RL = 27 / 50 = 54%
b) P = 2% x {[(50 / 5) x 5] x 35 } = 35
s = P / RL = 35 / 50 = 70%
2. Metodo contributivo
Poiché il tasso di sconto del valore futuro delle pensioni rZ è pari a 0, la pensione è data da:
P = MC/e(L)
dove MC è il montante contributivo individuale e e(L) è la speranza di vita del lavoratore al momento
del pensionamento.
Dati: δ = aliquota contributiva = 20%; r = tasso di rivalutazione dei contributi = 0; e(L) = 20 anni, si ha:
P = [20% x (30 x 10 + 40 x 20 + 50 x 5)] / 20 = 13,5
s = 13,5 / 50 = 27%
Esercizio 7 - Pensioni
Il Sig. A vive nel Paese X dove è in vigore un sistema pensionistico a ripartizione con metodo di calcolo
retributivo; egli lavora per due periodi percependo rispettivamente un salario di 100 e 110.
a) Calcolate la pensione del Sig. A, sapendo che la retribuzione pensionabile è pari alla media delle
retribuzioni dell’intera vita lavorativa (due periodi) rivalutate al tasso r pari al 4% e che il coefficiente di
rendimento è il 20%.
b) Come cambierebbe la pensione percepita dal Sig. A se nell’ambito del sistema a ripartizione venisse
applicato il metodo di calcolo contributivo? Rispondete utilizzando un’aliquota contributiva del 30%, un
tasso di rivalutazione dei contributi del 3%, una speranza di vita al momento del pensionamento pari a 3
anni e un tasso di sconto r z pari a zero.
Soluzione
a) Con il metodo retributivo la pensione è pari ad una percentuale (uguale al coefficiente di rendimento)
della retribuzione pensionabile moltiplicata per il numero di anni di contribuzione:
P  R p L
Nel caso in esame Rp è la media delle retribuzioni percepite durante l’intera vita lavorativa. Nell’ipotesi
che le retribuzioni crescano al tasso m e che siano rivalutate al tasso r, la retribuzione pensionabile si può
esprimere in generale come:
L
 R1 (1  m) j 1 (1  r ) L j
Rp 
j 1
L
dove R1(1+m)=R2, R1(1+m)2=R3,… R1(1+m)L-1=RL.
Date le retribuzioni ricevute dal sig. A nei due periodi di attività lavorativa, la retribuzione pensionabile
sarà semplicemente:
Rp 
R1 (1  r )  R2 100(1  0.04)  110

 107
2
2
La pensione sarà quindi:
P A = 0.2 x 107 x 2 = 42.8
b) Con il metodo contributivo, si costituisce un montante contributivo attraverso la capitalizzazione, ad un
tasso fissato convenzionalmente pari a r, dei contributi versati dal lavoratore. Ovvero:
MC 
L
 R (1  m)
1
( j 1)
(1  r ) ( L  j )
j 1
dove  è l’aliquota contributiva, r il tasso di rivalutazione dei contributi, m è definito come sopra e
R1(1+m)=R2, R1(1+m)2=R3,… R1(1+m)L-1=RL.
La pensione annua si ottiene poi (nell’ipotesi di tasso di sconto pari a zero) dividendo il montante
contributivo per la speranza di vita al momento del pensionamento, cioè:
P
MC
e(L)
Nel caso in esame, applicando un’aliquota contributiva  pari al 30% e un tasso di rivalutazione dei
contributi r pari al 3%, il montante contributivo è:
MC  R1(1  r )  R2  0.3 100(1  0.03)  0.3 110  63.9
Data e(L)=3, la pensione è quindi pari a:
PA 
63.9
 21.3
3
Esercizio 8 - Pensioni
Si consideri un paese in cui esiste un sistema pensionistico a ripartizione. In questo paese, il salario medio
pro-capite dei lavoratori attivi è w=100; la pensione media pro-capite costituisce l'80% del salario medio
pro-capite.
a) Sapendo che nel paese ci sono 5000 pensionati e 10000 lavoratori, si calcoli l'aliquota contributiva di
equilibrio del sistema.
b) Si immagini che nel paese arrivino 1000 giovani immigrati, che lavorano percependo un salario di
w=100 e pagano contributi (i pensionati continuano ad essere 5000 ed il rapporto tra la pensione media
pro-capite e il salario medio pro-capite è l’80%). Qual è la nuova aliquota contributiva di equilibrio?
c) Se volessimo mantenere la stessa aliquota contributiva calcolata nel primo punto anche dopo l'arrivo dei
1000 immigrati, a quanto ammonterebbe il rapporto tra la pensione media pro-capite e il salario medio
pro-capite?
Soluzione
L’equilibrio finanziario del sistema pensionistico (a ripartizione) richiede che:
 x w x NL = P x NP.
Con w = 100, P = 0.8 x w = 80,
avremo:
a)  = (P x NP) / (w x NL) = (80 x 5000) / (100 x 10000) = 0.4.
b) NL = 10000+1000 = 11000
 = (P x NP) / (w x NL) = (80 x 5000) / (100 x 11000) = 0,364.
L’aliquota contributiva diminuisce, perché aumenta il numero dei lavoratori che pagano contributi a parità di
numero di pensionati e di rapporto tra pensione media pro-capite e salario medio pro-capite.
c) P / w = ( x NL) / NP = (0.4 x 11000)/ 5000 = 0.88
Il rapporto tra pensione media pro-capite e salario medio pro-capite aumenta, perché aumenta il numero dei
lavoratori che pagano contributi a parità di numero di pensionati e di aliquota contributiva.
Domanda 1 (Tratto dal testo d’esame del 16/07/2008)
a) Definite il concetto di avversione al rischio e fornitene anche una rappresentazione grafica.
b) Elencate le condizioni a cui il mercato assicurativo privato è in grado di fornire un premio assicurativo
attuarialmente equo.
Soluzione
Si faccia riferimento al libro di testo pagg. 225-241.
Domanda 2 (Tratto dal testo d’esame dell’08/09/2006)
a) Che cosa si intende per sistema pensionistico a ripartizione e a capitalizzazione?
b) Derivate la condizione di equilibrio finanziario di un sistema pensionistico a ripartizione, descrivendo
sinteticamente le variabili da cui dipende.
c) Come rappresentereste, utilizzando la formula del punto precedente, il rischio demograficooccupazionale? A quali condizioni tale rischio ricade solo sui pensionati? A quali condizioni ricade solo sui
lavoratori?
d) Con riferimento al rischio demografico-occupazionale, quale è la principale novità introdotta nel sistema
pensionistico italiano dalla riforma Dini?
Soluzione
a) In un sistema a ripartizione il gettito contributivo annuale (a carico delle generazioni attive) è
destinato al finanziamento delle pensioni pagate nello stesso anno alle classi demografiche che
hanno cessato l’attività lavorativa. Non si ha dunque alcuna necessità di accumulare riserve per far
fronte al pagamento delle pensioni, né esiste alcun fondo intitolato ai singoli soggetti da utilizzare
per il calcolo della pensione.
In un sistema a capitalizzazione i contributi che ogni lavoratore versa nel periodo di attività sono
investiti sul mercato dei capitali. Nel periodo di pensionamento la pensione percepita dallo stesso
lavoratore è pari ai contributi versato aumentati del rendimento ottenuto dal loro impiego. Si ha
dunque accumulazione di riserve nel periodo che per ogni individuo intercorre fra il versamento dei
contributi e il pagamento della pensione.
b) L’equilibrio finanziario si realizza quando le entrate contributive sono uguali alle pensioni erogate.
Facendo riferimento alla definizione di sistema pensionistico a ripartizione data al punto precedente,
in tale sistema la condizione di equilibrio finanziario è la seguente:
MP  W  PNp   RlNl
dove:
MP monte pensioni,
W
monte salari,
α
aliquota contributiva (o di equilibrio per  
P
pensione media pro capite,
PNp
),
RlNl
Np numero di percettori di pensione,
Rl
salario medio pro capite,
Nl
numero degli attivi (percettori di salario e contribuenti).
c) Nella condizione di equilibrio finanziario precedentemente indicata il rischio demograficooccupazionale può essere valutato tramite il rapporto tra la popolazione pensionata e quella attiva
(Np/Nl).
Riscriviamo la condizione di equilibrio finanziario:
Np
Rl
 .
Nl
P
Supponiamo che si verifichi un invecchiamento della popolazione, per cui il rapporto Np/Nl aumenti.
Affinché si abbia equilibrio finanziario, anche il rapporto αRl/P deve aumentare. Supponendo che il
salario medio pro capite sia esogeno e non modificabile, è possibile agire o sull’aliquota contributiva
o sulla pensione media pro capite. Il rischio demografico-occupazionale ricade solo sui pensionati se,
a parità di aliquota contributiva, la pensione media diminuisce, per cui percepiscono minori rendite
pensionistiche. Al contrario, tale rischio ricade solo sugli occupati se l’aliquota aumenta, a parità di
P, in quanto dovranno versare maggiori contribuzioni.
d) Il rischio demografico dato dall’invecchiamento della popolazione, per cui il mantenimento della
generazione inattiva, in crescita, è a carico della generazione attiva, può essere neutralizzato
riducendo il numero dei pensionati attraverso il controllo del flusso d’ingresso nella generazione dei
pensionati. La riforma Dini aveva introdotto nel sistema pensionistico italiano la possibilità di andare
in pensione in una fascia di età compresa fra i 57 e i 65 anni. Il pensionamento anticipato era
comunque disincentivato dal metodo di calcolo della pensione, che legava in modo inversamente
proporzionale all’età il coefficiente di trasformazione del montante contributivo in rendita
pensionistica.