beatrice alberti - Digilander

Scuola di specializzazione per l’insegnamento nelle scuole
secondarie
II anno
Unità didattica di matematica:
COSTRUZIONE DEL CONCETTO DI
DERIVATA
Alberti Beatrice
Anno accademico 2005 – 2006
COLLOCAZIONE
V liceo scientifico
PREREQUISITI
1. Nozioni di geometria analitica riguardanti l’equazione di una retta.
2. Concetto di limite di una funzione in una variabile.
3. Dominio e continuità di una funzione.
OBIETTIVI DIDATTICI GENERALI
1. Inquadrare storicamente la nascita del calcolo infinitesimale.
2. Far acquisire consapevolezza agli studenti del fatto che si tratta di uno degli strumenti
fondamentali dell’analisi matematica.
3. Ricostruire concetti fisici già noti attraverso questo nuovo strumento.
OBIETTIVI DIDATTICI SPECIFICI
1. Saper definire la derivata di una funzione in un punto.
2. Saper calcolare la derivata di funzioni elementari.
3. Saper calcolare la derivata di funzioni, servendosi dei teoremi sulle derivate e sulle regole di
derivazione.
4. Saper determinare l’equazione della retta tangente in un punto ad una curva rappresentativa
di una funzione, applicando il significato geometrico della derivata.
5. Acquisire consapevolezza del fatto che la derivabilità è una condizione più restrittiva della
continuità.
6. Saper calcolare le derivate successive di una funzione.
7. Applicare con consapevolezza il concetto di derivata anche in altre discipline, specialmente
in fisica.
2
L’ORIGINE STORICA DELLA DERIVATA
Nella storia della matematica, i primi ad introdurre il concetto di derivata e di differenziale e a
sviluppare le relative regole di calcolo furono Newton e Leibniz. I problemi che in particolare
diedero origine al concetto di derivata sono quello delle tangenti e quello della velocità.
Il problema delle tangenti
Costruire la tangente ad una curva in un suo punto è un problema che risale addirittura agli antichi
greci e con il quale si sono misurati nel corso dei secoli molti matematici importanti, tra i quali gli
stessi Cartesio e Fermat.
Data una curva qualsiasi, la tangente alla curva in un suo punto P è data, approssimativamente, dalla
retta passante per il punto P e per un altro punto Q “vicinissimo” a P.
y
t
Q
P
x
Se vogliamo disegnare con una certa precisione la retta tangente ad una circonferenza in un suo
punto P, il metodo migliore è quello di tracciare il raggio OP e costruire la perpendicolare ad OP
passante per P.
Nel caso della circonferenza dunque esiste un metodo costruttivo efficace conosciuto fin
dall’antichità.
Anche per altre particolari curve si conoscevano delle tecniche per tracciare le tangenti, ma per
ognuna di esse la costruzione seguiva una strada particolare.
A partire dalla metà del 1600 , quando, con l’avvento della geometria analitica, si iniziarono a
studiare le curve in un riferimento cartesiano, furono elaborati dei metodi generali per determinare
la retta tangente ad una qualsiasi curva.
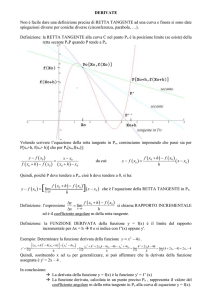
Il nostro obiettivo ora è quello di determinare l’equazione della retta tangente in un suo punto
P( x0 , y0 ) , ad una curva rappresentata analiticamente da un’equazione del tipo y=f(x), nell’ipotesi
che in tale punto la tangente esista.
3
Per definizione tale retta tangente rappresenta la posizione limite, se esiste, della retta che unisce P
con un altro punto Q(x,y) della curva, allorché si fa avvicinare Q indefinitamente a P.
y
t
Q
f(x 0 +h)
P
f(x 0 )
x
x0
x 0 +h
Sappiamo dalla geometria analitica che il coefficiente angolare della retta passante per P e Q è dato
da:
m
y  y0
x  x0
dove , tenendo conto dell’appartenenza di Q al grafico di f(x) e della sua vicinanza a P possiamo
sostituire le sue coordinate con le seguenti espressioni:
x  x0  x
y  f ( x)  f ( x0  x)
Dunque il coefficiente angolare della secante può essere scritto nella forma:
m
f ( x0  x)  f ( x0 )
.
x
Il coefficiente angolare della retta tangente sarà perciò:
lim
x 0
f ( x0  x)  f ( x0 )
.
x
4
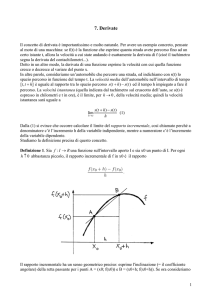
Velocità in un moto rettilineo qualunque
Consideriamo un oggetto puntiforme in moto rettilineo.
Indichiamo con x il tempo variabile e con y lo spazio percorso nel tempo x. Ovviamente lo spazio y
è una funzione della variabile x, poniamo dunque y=f(x).
Consideriamo ora la retta r
r
O
P
Q
Siano:
 O la posizione che il punto ha nell’istante iniziale x=0.
 P la posizione che ha all’istante x 0 .
 Q la posizione che ha all’istante x 0 +h.
Allora lo spazio PQ, percorso nell’intervallo di tempo h, è dato da:
f(x 0 +h) – f(x 0 ).
Ricordando la definizione di velocità media, il nostro punto materiale avrà percorso lo spazio PQ
con una velocità media pari a
f ( x0  h)  f ( x0 )
.
h
Volendo conoscere la velocità istantanea, ovvero la velocità che il punto assume in un preciso
istante, dobbiamo far tendere h a zero, dunque la velocità istantanea si trova calcolando:
lim
h 0
f ( x0  h)  f ( x0 )
.
h
Derivate
Abbiamo visto che per risolvere entrambi i problemi dobbiamo ricorrere a calcolare il limite
lim
h 0
f ( x0  h)  f ( x0 )
.
h
Tale limite, quando esiste ed è finito, viene detto derivata della funzione f(x) calcolata nel punto x 0 .
5
DEFINIZIONE Data una funzione y=f(x), definita almeno nell’intervallo
 a, b la funzione f si dice derivabile nel punto x0
lim
h 0
a, b , ed un punto x
0
se esiste finito il limite
f ( x0  h)  f ( x0 )
= f ' ( x0 )
h
dove h è un numero reale che rappresenta l’incremento dato alla variabile indipendente.
Il numero reale f ' ( x0 ) è chiamato derivata della funzione f nel punto di ascissa x0 .
 
DEFINIZIONE f si dice derivabile nell’intervallo a, b se è derivabile in ogni punto di questo
intervallo. La funzione f’ che ad ogni punto x 0 associa f’(x 0 ) è detta funzione derivata.
SIGNIFICATO GEOMETRICO : il valore della derivata f’(x) in un dato punto x0 , è uguale al
coefficiente angolare m della tangente alla curva di equazione y  f (x) , nel punto P( x0 , f ( x0 ) ).
RELAZIONE TRA CONTINUITA’ E DERIVABILITA’
Ci chiediamo ora se una funzione derivabile in un punto x 0 sia anche continua in tale punto.
La risposta ci viene data dal seguente:
Teorema Se una funzione y=f(x) è derivabile nel punto x 0 , allora è necessariamente continua in
quel punto.
Dim: dall’identità
f ( x0  h)  f ( x0 ) 
f ( x0  h)  f ( x0 )
h
h
essendo per ipotesi finito il limite
lim
h0
f ( x0  h)  f ( x0 )
 f ' ( x0 )
h
si ha
lim f ( x
h 0
0
 h)  f ( x0 )  lim
h 0
f ( x0  h)  f ( x0 )
 lim h
h
h 0
6
=
f ( x0 )  f ' ( x0 )  0  f ( x0 ) .
Ciò prova la continuità di f.
PROBLEMA: è vero il teorema inverso?
Proviamo a congetturare la risposta al problema aiutandoci con qualche esempio.
Esempio : y  x
La funzione nel punto x=0 è continua, infatti i limiti destro e sinistro della funzione coincidono col
valore che la funzione assume in tale punto. Vediamo cosa accade ai limiti destro e sinistro del
rapporto incrementale:
lim
h 0
lim
h 0 
0h  0
h
0h  0
h
1
 1
La funzione risulta dunque non derivabile nel punto x=0. Anche dal punto di vista geometrico
notiamo che nel punto x=0 la funzione non ammette un’ unica tangente, bensì due, rappresentate
dalle rette y=x e y=-x.
y
O
x
Dunque la condizione di continuità in un punto è una condizione necessaria ma non sufficiente
perché la funzione in quel punto sia derivabile.
7
Derivata di alcune funzioni elementari
Costruiamo insieme, utilizzando la definizione, le regole di derivazione di alcune funzioni
elementari:

Derivata di una funzione costante y  k
f ' ( x)  lim
h 0
k k
 lim 0  0 .
h 0
h
Questo risultato ammette una interpretazione geometrica semplice. Il grafico della funzione
y=k è una retta parallela all’asse x. La tangente a questo grafico coincide evidentemente in
ogni suo punto, con questa retta e perciò il suo coefficiente angolare è 0.

Derivata della funzione y  x .
xhx
 lim 1  1 .
h0
h0
h
f ' ( x)  lim
Anche questo risultato ammette una semplice interpretazione geometrica. Il grafico della
funzione y=x è la bisettrice del primo e terzo quadrante. La tangente a questo grafico è la
bisettrice stessa e dunque il suo coefficiente angolare è 1.

Derivata della funzione y  senx .
sen( x  h)  senx
senx cosh  cos xsenh  senx
 lim

h

0
h
h
senx (cosh  1)  cos xsenh
cosh  1
senh
 lim
 lim senx
 lim cos x
 senx  0  cos x  1  cos x
h0
h 0
h 0
h
h
h
f ' ( x)  lim
h 0
Analogamente si prova che D(cosx)= - senx.

Derivata della funzione y  ln x
ln( 1  h )
ln( x  h)  ln x
x  lim 1  x  ln( 1  h ) 
 lim
h0
h0
h
h
x h
x
f ' ( x)  lim
1

  lim ln 1 
h

0
x

x
h h 1

   ln lim 1 
h

0
x
x

x
h h 1
1
   ln e 
x
x
x
Quelli forniti sono soltanto alcuni esempi. In classe naturalmente cercherei di costruire con gli
studenti anche le regole di derivazione di alcune funzioni che qui ho tralasciato.
Osservazione: Evitare per quanto possibile di fornire ricette agli studenti, ma farle costruire a loro,
utilizzando la definizione e interpretando geometricamente il risultato ottenuto.
8
Derivata di una funzione composta
Siano date due funzioni:
y  f (u ) e u  g (x)
e supponiamo che, variando x nell’intervallo I, la funzione u=g(x) assuma valori appartenenti al
dominio della funzione y=f(u). Allora le due funzioni date definiscono la funzione composta
f g (x), che possiamo brevemente indicare con F(x) cioè poniamo:
F ( x)  f g ( x).
La derivata della funzione F(x) è espressa dalla relazione:
F ' ( x)  f ' (u )  g ' ( x) .
Naturalmente il teorema si estende anche al caso in cui le funzioni componenti siano più di due.
Costruiamo insieme alcune regole di derivazione di funzioni composte:

Dln f ( x) 

D f ( x)  n f ( x)

De f ( x )  e f ( x )  f ' ( x)

……
n
1
f ' ( x)
 f ' ( x) 
f ( x)
f ( x)
n 1
 f ' ( x)
Derivata di somma, prodotto e quoziente
Somma La derivata della somma di due o più funzioni derivabili esiste ed è uguale alla somma
delle derivate di queste funzioni.
Dim: Sia y  u ( x)  v( x) con u(x) e v(x) derivabili nel punto x.
Siano y, u, v rispettivamente gli incrementi delle funzioni y,u,v per il corrispondente
incremento x della variabile indipendente x.
Allora:
y  y  (u  u )  ( v  v ) .
Ora tenendo presente che y  u  v si ha che y  u  v quindi:
 y u  v


x x x
da cui, passando al limite per x  0 si ha:
9
y
u
v
 lim
 lim
 u 'v' .
x  0 x
x  0 x
x  0 x
y '  lim
Prodotto La derivata del prodotto di due funzioni derivabili esiste ed è uguale al prodotto della
derivata del primo fattore per il secondo, più il prodotto del primo fattore per la derivata del
secondo. Cioè se y  u  v allora:
y '  u 'v  u  v' .
Quoziente Cerchiamo di costruire la regola di derivazione del quoziente di due funzioni derivabili
u
utilizzando la regola di derivazione del prodotto. Sia y  . Questa la possiamo vedere scritta
v
1
come: y  u  . Dunque, applicando la regola di derivazione del prodotto, abbiamo:
v
1
 v'  u ' v  uv'
y '  u '  u    2  
.
v
v2
 v 
Derivata delle funzioni inverse
Teorema Sia y=f(x) una funzione reale della variabile reale x, continua e invertibile in un
intervallo I e sia x=g(y) la sua inversa.
Se f(x) è derivabile nel punto x 0  I, con derivata f’(x 0 )  0 , allora anche g(y) è derivabile nel
punto y 0 =f(x 0 ) e si ha:
g ' ( y0 ) 
1
.
f ' ( x0 )
Osservazione: si tratta di un teorema la cui applicazione è talvolta richiesta in alcuni quesiti delle
prove di maturità. Per evitare la pesantezza della trattazione evitiamo di darne la dimostrazione e
vediamo invece qualche applicazione.
Determiniamo la derivata della funzione y= arcsenx.
Tale funzione è l’inversa della funzione x=seny. In base al teorema appena enunciato si ha:
Darcsenx 
Ora
cos y   1  sen 2 y   1  x 2
1
1

.
Dsenx cos y
e poiché y
  
varia nell’intervallo  ,  , si ha
 2 2
cos y  1  x 2 .
Dunque Darcsenx 
1
1  x2
.
10
Analogamente si prova che
D arccos x  
Darctgx 
1
1  x2
.
1
1  x2
La formula che esprime la derivata dell’arcotangente è molto interessante perché fornisce un
secondo esempio (il primo era il logaritmo) di funzione trascendente avente per derivata una
funzione razionale.
11
Rivisitiamo alcuni concetti di fisica
Lo studio del concetto di derivata ci permette di riconsiderare da una prospettiva diversa alcuni
concetti di fisica affrontati negli anni precedenti. Vediamone alcuni.
Velocità di un corpo che si muove di moto rettilineo uniforme:
v
 v  lim st  dsdt
s
t
t  0
Secondo principio della dinamica:


F  m a



dp
F


dt

dove p rappresenta la quantità di moto di un corpo di massa m.
Intensità di corrente in un conduttore:
I 
q
t

q dq

t  0 t
dt
I  lim
.
Notiamo che in tutti e tre i casi la variabile rispetto alla quale deriviamo è il tempo.
12
ATTIVITA’ DI RECUPERO E APPROFONDIMENTO
Le difficoltà in questo ambito possono essere legate essenzialmente a:
 Scarsa manualità nell’uso dell’algebra.
 Difficoltà nel cogliere a fondo la differenza tra continuità e derivabilità.
L’uso di Derive può aiutare a visualizzare e padroneggiare meglio tale difficoltà.
Un'altra attività di approfondimento potrebbe essere l’uso di Cabrì per mostrare le varie costruzioni
usate nel corso della storia per disegnare le tangenti.
VERIFICA
PRIMA PARTE
1) Se una funzione è derivabile in x0 , allora ivi è:
a) continua
b) non necessariamente continua
c) discontinua
2) La funzione y  ln x , nel punto x=0 è:
a) continua
b)derivabile
c) discontinua
3) La funzione y  senx , nel punto x   è:
a) continua
b) derivabile
c) non è definita
4) La derivata della funzione y  e
a) - e
x2
b) -2 e
x2
x2
è:
c) 2 x e
x2
d)- 2 x e
x2
e)- 2 x e
2 x
SECONDA PARTE
5) Trovare le equazioni delle tangenti alla parabola y  x 2  3x  2 nei punti
ove interseca gli assi coordinati.
6) Determinare il numero dei punti del grafico della funzione
f ( x)  1  12  e x  12 x  3x 2  2 x3 , nei quali la tangente è parallela all’asse x.
7) In un riferimento cartesiano ortogonale Oxy, il moto del punto P è
definito dalle equazioni:
t

x  e

 t

y  e
con  costante positiva. Determinare:
a) la traiettoria di P
b) la velocità e l’accelerazione al tempo t.
13
14