nozioni di insiemistica

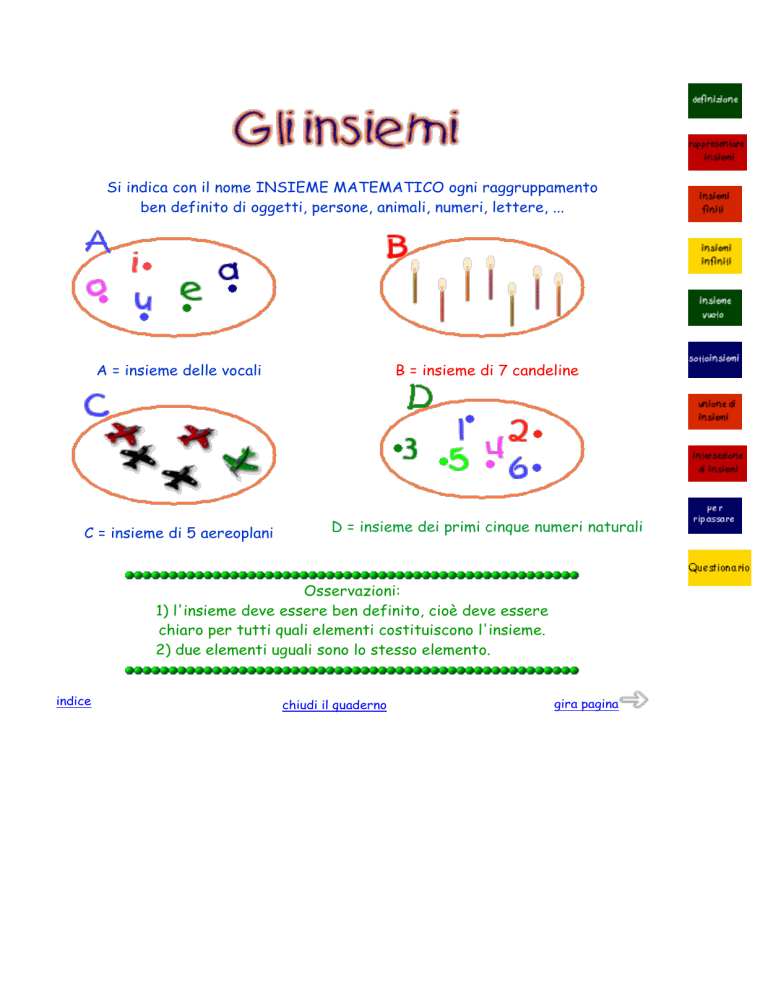
Si indica con il nome INSIEME MATEMATICO ogni raggruppamento
ben definito di oggetti, persone, animali, numeri, lettere, ...
A = insieme delle vocali
B = insieme di 7 candeline
C = insieme di 5 aereoplani
D = insieme dei primi cinque numeri naturali
Osservazioni:
1) l'insieme deve essere ben definito, cioè deve essere
chiaro per tutti quali elementi costituiscono l'insieme.
2) due elementi uguali sono lo stesso elemento.
indice
chiudi il quaderno
gira pagina
Consideriamo l'insieme costituito dalle vocali dell'alfabeto;
come possiamo RAPPRESENTARE questo insieme?
1°MODO :
I DIAGRAMMI DI VENN
Gli insiemi si rappresentano con una linea chiusa, un recinto in cui mettere gli elementi
dell'insieme
La linea chiusa si chiama "DIAGRAMMA DI VENN"
Gli elementi vengono disegnati dentro il diagramma:
Solo gli elementi a, e, i, o, u appartengono agli insieme.
2° MODO:
"RAPPRESENTAZIONE PER ELENCAZIONE"
Per indicare un insieme e i suoi elementi senza i diagrammi di Venn si scrive:
A = { .................. }
A è il nome dell'insieme e, al posto dei puntini, si scrivono gli elementi separati da virgole
A = { a, e , i , o , u }
3° modo:
"RAPPRESENTAZIONE PER CARATTERISTICA"
Gli elementi dell'insieme si indicano con una proprietà che li identifica in modo preciso:A
{ x / x è una vocale}
si legge: l'insieme A è formato da tutti gli elementi x tali che x è una vocale.
La caratteristica degli elementi è: " essere una vocale".
Questa rappresentazione si usa soprattutto quando gli elementi sono molto numerosi e
sarebbe difficile e lungo elencarli tutti.
Esempio:
B = { b / b è una mammifero}
=
Un insieme è FINITO se è contiene un numero limitato di elementi.
Osserva i seguenti esempi che rappresentano insiemi finiti:
A=
{ a /a è un numero naturale minore di 6 }
A = { 1, 2, 3, 4, 5 }
A = { primavera, estate, autunno, inverno
A=
}
{ a / a è una stagione}
Altri esempi di insiemi finiti:
A=
{ a / a è un numero naturale maggiore di 15 e minore di 30}
A = {16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 }
B=
{ b / b è una lettera della parola "divertimento"}
B = { d, i, v, e, r, t, m, n, o} ( RICORDA! gli stessi elementi non si ripetono! )
C = { c / c è un abitante del comune di Asti}
Un insieme è INFINITO se è contiene un numero infinito di elementi.
Osserva i seguenti esempi che rappresentano due insiemi infiniti:
B=
N=
N=
{ a /a è una stella del cielo}
{ n / n è un numero naturale }
{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... }
Altri esempi di insiemi infiniti:
A=
{ a /a è un numero intero maggiore di 100} = { 101, 102, 103, 104, 105, ... ,...}
B=
{ b /b è un numero pari} = { 0, 2, 4, 6, 8, 10, 12, 14, ... , ...}
C=
{ c /c è una numero intero multiplo di 7} = { 0, 7, 14, 21, 28, 35, 42, ... , ...}
Un insieme è FINITO se è contiene un numero limitato di elementi.
Osserva i seguenti esempi animati che rappresentano insiemi finiti:
A=
{ a /a è un numero naturale minore di 6 }
A = { 1, 2, 3, 4, 5 }
A=
{ primavera, estate, autunno, inverno }
A = { a / a è una stagione}
Altri esempi di insiemi finiti:
A = { a / a è un numero naturale maggiore di 15 e minore di 30}
A = {16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 }
B = { b / b è una lettera della parola "divertimento"}
B = { d, i, v, e, r, t, m, n, o} ( RICORDA! gli stessi elementi non si ripetono! )
C = { c / c è un abitante del comune di Asti}
Un insieme è VUOTO se non contiene elementi;
si indica con il simbolo
oppure { }.
Osserva il seguente esempio animato che rappresenta un insieme vuoto:
A=
{ a /a è un mese di 32 giorni}
A=
={ }
Altri esempi di insiemi vuoti:
A = { a / a è un numero naturale maggiore di 5 e minore di 6}
A=
B = { b / b è un mammifero con sei zampe}
B=
C = { c / c è un asino che vola}
C=
n insieme B si dice SOTTOINSIEME PROPRIO di un insieme A se ogni elemento di B
ppartiene ad A, ma c'è almeno un elemento di A che non appartiene a B.
ESEMPIO n° 1
A = { a/a è un mese dell'anno }
B = { b/b è un mese dell'anno di 30 giorni }
B è sottoinsieme di A
oppure
B è contenuto in A
oppure
B c A
:
ESEMPIO n° 2
A = { farfalla, mosca, ragno, coleottero, scarabeo}
B = { b/b è un insetto dell'insieme A con le ali}
B è sottoinsieme di A
B è contenuto in A
B
c
A
Casi particolari:
gni insieme A possiede due sottoinsiemi speciali che si chiamano sottoinsiemi impropri di A: lo
esso insieme A e l'insieme vuoto.
Si dice UNIONE di due insiemi A e B l'insieme formato da tutti gli elementi di A
e da tutti gli elementi di B, senza ripetere due volte gli elementi uguali.
U è il simbolo utilizzato per indicare l'unione
Esempio:
A={a,b,c}
B={c,d,e}
AUB={a,b,c,d,e}
osserva come l'elemento "c" che appartiene sia ad A che a B viene considerato SOLO
UNA VOLTA nell'insieme UNIONE.
Altri esempi di unione di insiemi:
A=
{ pesce , farfalla , mosca}
B = { foglia , ragno , pigna }
A U B = { pesce , farfalla , mosca , foglia , ragno , pigna }
A=
{ pesce , farfalla , mosca}
B = { pesce , foglia , pigna }
A U B = { pesce , farfalla , mosca , foglia , pigna }
(il pesce non si ripete due volte; gli elementi dell'insieme AUB sono cinque e non sei)
A=
{ pesce , farfalla , mosca}
B = { pesce , mosca}
A U B = { pesce , farfalla , mosca } = A
( OSSERVA: se B è sottoinsieme di A allora AUB coincide con A)
Si dice INTERSEZIONE di due insiemi A e B l'insieme formato da tutti gli
elementi che appartengono sia ad A che a B.
è il simbolo utilizzato per indicare l'intersezione.
Esempio:
A={1,2,3}
B = { 3 , 4 , 5}
A B={3}
Guarda con attenzione l'animazione e osserva l'intersezione di A e B.
Altri esempi di intersezione di insiemi:
A = { pesce , farfalla , mosca}
B = { pesce , foglia , pigna }
A B = { pesce }
(il pesce è l'unico elemento comune ad A e a B)
Esempio
A = { pesce , farfalla , mosca}
B = { pesce , mosca}
A B = { pesce , mosca } = B
( OSSERVA: se B è sottoinsieme di A allora A B coincide con B )
Esempio
A = { pesce , farfalla , mosca}
A
B = { foglia , ragno , pigna }
B=
A e B non hanno elementi nessun elemento in comune
Se B A =
allora A e B sono DISGIUNTI )
(schema riassuntivo)
Si indica con il nome INSIEME MATEMATICO ogni raggruppamento
ben definito di oggetti, persone, animali, numeri, lettere, ...
Gli insiemi si possono rappresentare in tre modi:
1° modo:
2° modo:
3° modo:
I DIAGRAMMI DI VENN
"RAPPRESENTAZIONE PER ELENCAZIONE"
"RAPPRESENTAZIONE PER CARATTERISTICA"
Un insieme è FINITO se è contiene un numero limitato di elementi.
Un insieme è INFINITO se è contiene un numero infinito di elementi.
Un insieme è VUOTO se non contiene elementi;
si indica con il simbolo
oppure { }.
Un insieme B si dice SOTTOINSIEME PROPRIO di un insieme A se ogni elemento
di B appartiene ad A, ma c'è almeno un elemento di A che non appartiene a B.
Ogni insieme A possiede due sottoinsiemi speciali che si chiamano sottoinsiemi
impropri di A: lo stesso insieme A e l'insieme vuoto.
Si dice UNIONE di due insiemi A e B l'insieme formato da tutti gli
elementi di A e da tutti gli elementi di B, senza ripetere due volte gli
elementi uguali.
U è il simbolo utilizzato per indicare l'unione
Si dice INTERSEZIONE di due insiemi A e B l'insieme formato da tutti
gli elementi che appartengono sia ad A che a B.
è il simbolo utilizzato per indicare l'intersezione.
INSIEMISTICA
I simboli dell'insiemistica sono:
significa "appartiene"
significa "non appartiene"
significa "è contenuto" oppure " è
incluso" oppure " è sottoinsieme di"
significa "insieme vuoto"
U è il simbolo dell'UNIONE
è il simbolo dell'INTERSEZIONE