Introduzione alla LOGICA MATEMATICA

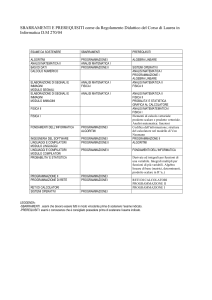
• Struttura del corso: logica e combinatoria + algebra
astratta. Gli studenti dei corsi precedenti possono
optare tra vecchio e nuovo programma.
• fino all’inizio di novembre logica e combinatoria full
immersion, dopo prevalentemente algebra
• Orari: lunedì 8.30-11.30, martedì 8.30-10.30,
giovedì 8.30-11.30.
• Esami: due scritti + un orale. Esoneri: il primo subito
prima di Natale, il secondo a metà gennaio.
• Materiali. Logica: tutorials e slides power point in
rete. Testo di algebra
• e-mail: [email protected]
www.dm.uniba.it/Members/borzacchini
Tutorials e Presentazioni pptx
(che però talora cambio)
F.A.Q.
Risoluzione dei problemi degli scritti
Risultati degli scritti
LINK UTILI.
Un corso teorico del prof. G.Lolli:
http://homepage.sns.it/lolli/dispense07.htm
Tutorials con esercizi:
http://logic.philosophy.ox.ac.uk/main.htm
http://courses.umass.edu/logic/homework/
http://www.cs.odu.edu/~toida/nerzic/content/logic/intr_to_logic.html
• Introduzione al ‘pensiero formale’, alla
manipolazione dei segni, all’idea rigorosa di
dimostrazione e al ragionamento algoritmico,
• sia per preparare allo studio della matematica, sia
perché il computer è una ‘macchina’ che manipola
segni, sia perché la logica è alla base della computer
science
• pre-nozioni zero, dimostrazioni zero, ma studieremo
che cos’è la dimostrazione?
• Esame da fare subito! Se no diventa un incubo!
• i corsi di matematica in senso stretto cominciano
con la parte di algebra, la logica dovrebbe anche
aiutarvi ad affrontarli meglio
Introduzione
alla
LOGICA MATEMATICA
Corso di Matematica Discreta.
Corso di laurea in Informatica.
Prof. Luigi Borzacchini
I. I segni, gli algoritmi, i linguaggi, la
rappresentazione, sintassi e semantica.
Che vuol dire matematica discreta?
• Discreta è la matematica che tratta di numeri interi
e razionali, segni algebrici, insiemi finiti di punti.
• Continua è la matematica che tratta di figure
geometriche, di numeri reali, di applicazioni fisiche.
• Nell’antichità e nelle scuole elementari la
matematica discreta è l’aritmetica e quella continua
è la geometria: matematiche che trattano attributi
dell’esperienza comune. Ma è noto agli storici della
scienza e agli psicologi cognitivi che quattro secoli fa
è nata una matematica diversa, in cui si trattano
‘enti’ più strani: segni algebrici, equazioni, serie,
l’infinito, etc.
Matematica e computer science
- Matematica col computer
La realtà è (quasi sempre) continua: modelli
matematici, matematica del continuo, calcolo
numerico, calcolo delle probabilità, ricerca operativa
- Matematica del computer
Il computer, il linguaggio e il cervello sono discreti:
logica matematica, combinatoria, algebra, teoria
degli algoritmi e linguaggi formali: il mondo dei segni
Storicamente la logica e la matematica sono alle radici
della computer science: il primo computer con
programma registrato si deve a Charles Babbage, un
matematico inglese dell’Ottocento.
Il modello teorico degli algoritmi e dello stesso
computer è la macchina di Turing, l’attuale
architettura dei computer è sostanzialmente ascritta a
John von Neumann: ebbene Turing e von Neumann
erano logici e matematici di un secolo fa, legati al più
importante approccio alla indagine matematica
all’inizio del secolo: il “formalismo”. Ed anche oggi,
tutti gli aspetti sia teorici che applicativi della
computer science hanno una base matematica,
più precisamente in un approccio ‘formalista’
Il pensiero formale
Che intendiamo per ‘formale’? La ‘forma’ contrapposta
al ‘contenuto’? Come nei temi di italiano : il contenuto
è buono, ma la forma è sgrammaticata.
O alla ‘materia’? un tavolo fatto di legno e di forma
rettangolare.
O alla ‘sostanza’? Come nel diritto in cui il ‘vizio di
forma’ annulla un procedimento sostanzialmente
ineccepibile.
‘Formale’ in matematica e nella computer science sta
per sintattico, basato sulla sola manipolazione di segni
secondo regole, mentre semantico è relativo al
significato.
L’anima logico-matematica del
computer
• Il computer attuale nasce circa 70 anni fa dalla
collaborazione di due classi di scienziati: gli
‘elettronici’ e i ‘logici-matematici’ che fornirono
rispettivamente il corpo e l’anima del computer.
• L’elettronica ha subito cambiamenti epocali: dai
relais alle valvole, ai transistor, ai microchip sempre
più piccoli e potenti, tanto che questa evoluzione di
misura in ‘generazioni’
• L’anima logico-matematica invece è rimasta sempre
la stessa: lo schema della macchina universale di
Turing e l’architettura di von Neumann.
La logica, gli algoritmi, l’argomentazione
La logica tratta delle argomentazioni
razionali, in tutti i campi, dalla filosofia
alla matematica, dal diritto alla tecnica.
C’è una qualche somiglianza tra i calcoli
(le operazioni, gli algoritmi) e i
ragionamenti, ad esempio filosofici?
Per Leibniz (XVII secolo) si!
Il computer nasce dall’idea che ogni argomentazione logica,
ogni dimostrazione, è un algoritmo, e che ogni calcolo, ogni
algoritmo è una dimostrazione, una argomentazione logica
I SEGNI
• Ma che cosa sono i segni?
• Qualcosa che sta per qualcos’altro (il significato):
• L’effetto per la causa (il fumo per il fuoco, gli
occhi lucidi per la febbre, etc.)
• Per convenzione (il fischio dell’arbitro per il fallo,
le lettere per i suoni alfabetici, etc.)
• Per analogia o similitudine (silhouette di uomini
e donne sui bagni, segnali stradali: ,
, etc.)
• Il significato è preciso, fisso, ben definito.
… e poi c’è la x, il segno algebrico
I segni matematici e logici
• La x è l’incognita, quello che non si sa e quindi
non significa niente, non sappiamo neanche se
sia un numero, un cliente, uno studente…
Oppure è generico o variabile
• I segni algebrici non hanno un vero ‘significato’.
• x+2=5 mi dice che x=3. Anche se supponiamo di
sapere che cosa ‘significano’ +, 2, =, 5, da dove
ricaviamo che x ‘significa’ o ‘denota’ il 3?
Il significato che i segni matematici hanno perso,
in realtà è stato ‘trasferito’ agli algoritmi che
trattano segni, e gli algoritmi manipolano solo
segni
x+2=5 x=5-2 x=3
Sintassi e Semantica
• La distinzione tra sintassi e semantica caratterizza
la logica matematica attuale rispetto all’antica
logica aristotelica
• La sintassi tratta della struttura formale delle
espressioni, a prescindere dal significato. «A è un B»
è una struttura formale che descrive il tipo più
comune di giudizi. Ma non sappiamo se sia vera o
falsa, dovremmo conoscere il significato di A e B.
• Il significato si associa a espressioni. In italiano «il
cane mangia la carne» ha un significato, «cane» ha
un significato, «c» non ha alcun significato.
La deduzione e la verità
• Le deduzioni hanno aspetti tanto semantici
(contenutistici) che sintattici (formali).
Ad esempio da «Michele è brindisino» e «Tutti i
brindisini sono pugliesi» si deduce «Michele è
pugliese», ed il significato è chiaro ed evidente.
Ma se dico: «Michele è un sarchiapone» e «Tutti i
sarchiaponi sono sesquipedali», posso dedurre
formalmente «Michele è sesquipedale», ma il
significato è oscuro: la deduzione è in questo caso un
fatto solo sintattico, relativo ad una forma del tipo «a
è un B», «tutti i B sono C», e dunque «a è un C».
Il calcolo
• Anche i calcoli hanno aspetti tanto semantici che
sintattici.
• Ad esempio il problema: <ogni cartone contiene 6
uova, la mamma ha comprato 4 cartoni. Quante
uova ha comprato?>, la risposta è 24
• Ma se il problema è: <ogni struck ha 6 stiff e ho 4
struck. Quanti stiff ho?>, la risposta è 24.
• Anche qui la stessa differenza: da un punto di vista
sintattico i due problemi sono identici e si riducono
al calcolo 64 = 24, ma semanticamente il primo è
comprensibile il secondo no.
Ragione formale (sintattica):
«Ragionare senza comprendere»
• Ragionare tramite la sola manipolazione di segni
secondo regole. E’ una capacità soltanto umana.
• Gli animali hanno un qualche linguaggio, una certa
logica concreta, anche una semplice aritmetica di
piccoli numeri. Ma non hanno una ragione formale.
• La ragione formale e la logica formale sono assenti
anche nelle popolazioni cosiddette ‘primitive’, e
storicamente appare insieme alla alfabetizzazione.
• E il computer è la macchina sintattica, che possiede
solo la ragione formale: l’uomo moderno è l’uomo
primitivo + il computer + la loro fusione.
Gli algoritmi e le macchine.
• L’algoritmo è una macchina sintattica.
• Il computer è la macchina sintattica universale.
Input:
dati
algoritmo
Output:
soluzione
Sintattica perché consiste nel manipolare segni secondo
regole fisse indipendenti dal significato dei segni.
Esistono problemi risolubili meccanicamente, e problemi che
richiedono l’assemblaggio non ovvio di diverse procedure.
E soprattutto ‘creare’ algoritmi non è una procedura
meccanica, e non lo è adattarli ai problemi concreti. Può
essere facile o difficile, ma è spesso un’attività creativa, in
quanto il problema deve essere ‘rappresentato’ formalmente
La rappresentazione (semantica)
La rappresentazione iconica
La rappresentazione sintattica
CASA
𝐴 = 𝜋𝑟 2
Nessuna somiglianza, non è
analitica (la lettera C di CASA
non corrisponde a nessuna
parte di una casa), ha natura
linguistica, dipende da un
particolare linguaggio, ma può
rappresentare anche termini
astratti.
Talora si usano insieme i due tipi di
rappresentazione
Si basa sulla somiglianza, è
analitica (il camino nella
immagine della casa è la
immagine di un camino), è
universale, ma ha difficoltà
coi termini astratti, giustizia,
verità, negazione, essere, …
Il triangolo semiotico
Le parole (rosso) hanno una
intensione (la ‘rossità’) ed una
estensione (l’insieme degli
oggetti rossi). Il termine
‘pari’ ha come intensione la
definizione (divisibile per 2) e
come estensione {2,4,6,8,10,…}
Sino dagli antichi Greci la
rappresentazione sintattica si
è strutturata come un
triangolo i cui tre vertici sono
la realtà, la mente e il
linguaggio.
Le relazioni interne al
linguaggio caratterizzano la
sintassi, mentre le relazioni
tra linguaggio e realtà
caratterizzano la semantica,
il regno del significato.
Le primitive e i segni interpretabili
• Se in algebra numerica scrivo a+b=b+a (la proprietà
commutativa), i segni usati sono a, b, +, =. Ma
hanno un ruolo diverso i primi due dai secondi due.
• Trattando di numeri, a e b sono segni interpretabili,
posso assegnare loro il significato che desidero: a
può essere interpretato come 3 o 7 o 3418, …. E così
anche b.
• + e = hanno invece un significato immutabile, sono
delle primitive dell’aritmetica, non sono
interpretabili, ed il loro ‘significato’ è dato dalle
regole della manipolazione algebrica.
Il computer manipola segni
Che ‘significa’ un segno quando lavori col computer?
Solo l’uso che di quel segno faranno il sistema
operativo o il compilatore, che sono gli algoritmi che
manipolano i segni sul computer.
Sono segni interpretabili gli indici, i parametri, gli
indirizzi, etc., assegnabili a piacere, altri sono delle
primitive, il cui significato è ‘built in’, fissato nel
compilatore dal modo con cui esso li manipola: if-thenelse, for, while, le operazioni logico-aritmetiche, etc.
Non esistono algoritmi senza segni da manipolare e
non esistono segni senza algoritmi che li manipolano
I linguaggi di rappresentazione
Realtà e Segni sono diversi
La rappresentazione
sintattica è un linguaggio
per esprimere fatti e
deduzioni ottenute da
essi tramite segni.
Ogni linguaggio di
rappresentazione deve
quindi fornire sia una ‘rappresentazione’ sintattica di ogni
possibile fatto (come proposizione), sia un ‘calcolo’ per
dedurre dai fatti (come inferenza)le loro possibili
conseguenze logiche.
Linguaggio e Calcolo
• Leibniz si era accorto che la rappresentazione
sintattica aveva questo grande vantaggio: era sia un
linguaggio di rappresentazione che un calcolo.
• Ogni individuo e ogni fatto del mondo da
rappresentare poteva essere rappresentato tramite
i simboli: la rappresentazione era universale.
• Il divenire e le deduzioni in tale mondo potevano
essere ‘simulate’ con la manipolazione dei segni
secondo regole: la rappresentazione era un calcolo.
• L’algebra, l’analisi, i linguaggi di programmazione, e
soprattutto la logica e gli algoritmi sono linguaggi di
rappresentazione, linguaggi formali.
Alfabeti e linguaggi formali
• Un alfabeto S è un insieme di segni, ad esempio:
{a, b, c, d, … , u, v, z} è l’alfabeto italiano
• Una sequenza finita di segni di un alfabeto è
un’espressione (o parola) dell’alfabeto: bdactru
Indicheremo con S* l’insieme di tutte le parole.
• Una parte L di S* è detta un linguaggio. Ad
esempio {abaco, abate, abbinare, …, zucca,
zuzzurellone} è il lessico del linguaggio italiano.
I linguaggi naturali hanno un’origine storica e non sono
formati tramite regole precise. I linguaggi formali sono
stati costruiti artificialmente e sono formati tramite
regole precise
• Un linguaggio può essere usato come alfabeto per un
linguaggio più complesso:
• Alfabeto italiano  Lessico italiano (parole) nel vocabolario
• Lessico Italiano  Linguaggio italiano (frasi)
• Frasi in italiano  Libri in italiano
• Cifre  Numeri interi
• Numeri interi, {+, -, , :, (, )}  Espressioni
• Espressioni  Sequenza di espressioni (eserciziario)
• Cifre, simboli e lettere (tastiera) Istruzioni in C++
• Istruzioni in C++  Programmi in C++
• Programmi in C++  Libreria programmi in C++
• I linguaggi finiti sono descritti elencandone le parole.
• Ma come si può descrivere un linguaggio infinito?
Grammatiche Generative
• Il linguaggio formale è dato da una grammatica
generativa che produce tutte e sole le espressioni
del linguaggio (formule ben formate, fbf).
Esempio: i numeri
Alfabeto 1: {|}
Grammatica: i) sono numeri | e i numeri seguiti da |
ii) nient’altro è un numero.
Linguaggio: {|, ||, |||, ||||, |||||, ||||||, ….}
Alfabeto 2: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, le cifre
Grammatica: i) sono numeri le cifre e i numeri seguiti
da una cifra ii) nient’altro è un numero.
Linguaggio: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,…}
Esempio: le espressioni aritmetiche
Alfabeto: {+, -, , :, (, ), 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Grammatica: i) sono numeri le cifre e le cifre seguite
da un numero [così generiamo tutti i numeri], ii) sono
espressioni tutti i numeri, iii) Se E è una espressione,
-E è una espressione, iiii) Se E è una espressione, (E +
E), (E - E), (E : E), (E  E) sono espressioni.
iiiii) nient’altro è una espressione.
Distinguiamo ‘sostituzione’ e ‘rimpiazzamento’ di un
simbolo in una espressione formale. La ‘sostituzione’
avviene ovunque con lo stesso simbolo, come in
algebra, il ‘rimpiazzamento’ si può fare sostituendo
simboli distinti: le due E in E+E possono essere due
espressioni qualsiasi anche diverse.
Simboli ausiliari e Rimpiazzamento
• Usando i simboli ausiliari Cifra, Numero ed
Espressione, che non compariranno nel linguaggio,
possiamo scriverla nella forma:
• Cifra  0/1/2/3/4/5/6/7/8/9
• Numero  Cifra / Cifra Numero
• Espressione  Numero / - Espressione /
(Espressione + Espressione) / (Espressione :
Espressione) / (Espressione  Espressione)
ove / vuol dire ‘oppure’ e i simboli ausiliari a destra di
 possono essere ‘rimpiazzati’ anche da termini
diversi.
• Così che possiamo costruire L’Espressione
(-37  (125 + 7)) generandola:
• Espressione  (Espressione  Espressione) 
• (- Espressione  (Espressione + Espressione)) 
• (- Numero  (Numero + Numero)) 
• (- Cifra Numero  (Cifra Numero + Cifra)) 
• (- Cifra Numero  (Cifra Cifra Numero + Cifra)) 
• (- Cifra Cifra  (Cifra Cifra Cifra + Cifra)) 
• (- 37  (125 + 7))
Esempio: le espressioni algebriche
• Alfabeto: {+, -, , :, (, ), 0, 1, 2, 3, 4, ….., x, y, z, ….}
• Grammatica: i) sono espressioni tutti i numeri e
tutte le variabili [diamo per già generati i numeri]
• ii) Se E è una espressione, -E è una espressione
• iii) Se E1 e E2 sono espressioni, (E1 + E2), (E1 - E2),
• (E1 : E2), (E1  E2) sono espressioni.
• iiii) nient’altro è una espressione.
Esempio: (((x+3)  (y-x)) : ((x  y) + 3)). Generiamola:
E  (E1 : E2)  ((E11  E12) : (E21 + E22))

(((E111+ E112)  (E121- E122)) : ((E211 E212)+ E22))

((( x + 3 )  ( y - x )) : (( x  y) + 3 ))
Espressione scritta come un albero,
senza parentesi
•
•
•
•
•
•
• E111
• x
E
:
E1

E11
E12
E21
+

E112 E121 E122 E211
3
y
x
x
E2
+
E22
E212
y
E22
3
•
•
•
scriviamo le espressioni ma
intendiamole come alberi
10/11
:
10
11

5
•
2
+
2
+
4
8
2
2

4
•
x
3 y
x
x
y
3
• ((( x + 3 )  ( y - x )) : (( x  y ) + 3 ))
• e il calcolo si effettua dal basso verso l’alto:
prova a porre x=2 e y=4, ottenendo 10/11