primo membro

Identità ed equazioni
• Una identità è una uguaglianza tra due espressioni
letterali che è vera per qualsiasi valore numerico che si
può attribuire alle lettere.
(x+2x=3x
è una identità, perché sempre vera)
• Una equazione è una uguaglianza tra due espressioni
letterali che è vera soltanto per alcuni valori numerici
che si possono attribuire alle lettere. I valori che
rendono valida l'uguaglianza si dicono soluzioni
dell'equazione, le lettere alle quali si sostituiscono i
valori si dicono incognite.
(x+2 = 2x
05/06/2017
è un'equazione)
Matematizzazione di semplici situazioni
problematiche ( M.P.)
1
IL Linguaggio delle Equazioni
• In un'equazione si distingue tra primo membro (i
termini prima del segno =) e secondo membro (i
termini dopo il segno =). Primo membro e secondo
membro sono separati dal segno =.
3x +2 = 2x +3
• Le lettere che compaiono in un'equazione si dicono
incognite. I termini che non contengono le lettere
incognite si dicono termini noti
• Il valore numerico (o i valori) dell'incognita che
soddisfano l'equazione si dicono soluzioni
3x+2=2x+3 ha per soluzione x=1, infatti 3·1+2=2·1+3
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
2
Principi di equivalenza
I principi di equivalenza sono due teoremi
fondamentali della teoria delle equazioni, essi
permettono di trasformare un’equazione
complicata in un’equazione molto semplice.
Primo Principio
Secondo principio
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
3
Equazioni equivalenti
• Due equazioni che hanno le stesse soluzioni si
dicono equivalenti.
Le equazioni x-2=3 e x-1=4 sono equivalenti, in
quanto hanno la stessa soluzione.
x=5
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
4
Primo principio di equivalenza
Addizionando o sottraendo a entrambi i
membri di un'equazione lo stesso numero si
ottiene un'equazione equivalente a quella
data.
I membro
=
II membro
Equivalente a
I membro
05/06/2017
+
=
II membro
Matematizzazione di semplici situazioni
problematiche ( M.P.)
+
5
La bilancia e il primo principio
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
6
Regola del trasporto
In un'equazione si può trasportare un termine
da un membro all'altro purché lo si cambi di
segno; l'equazione ottenuta è un'equazione
equivalente a quella di partenza.
4x + 5
=
2x +8
Equivalente a
4x
05/06/2017
=
2x+8- 5
Matematizzazione di semplici situazioni
problematiche ( M.P.)
7
Eliminazione dei termini uguali
Se uno stesso termine compare sia al primo
membro dell'equazione sia al secondo
membro è possibile semplificare l'equazione
eliminando i due termini uguali.
4x + 5
=
2x +8+ 5
Equivalente a
4x
05/06/2017
=
2x+8
Matematizzazione di semplici situazioni
problematiche ( M.P.)
8
Secondo principio di equivalenza
Moltiplicando o dividendo per uno stesso
numero (diverso da zero) entrambi i membri
di un'equazione si ottiene un'equazione
equivalente a quella di partenza.
I membro
=
II membro
Equivalente a
I membro
05/06/2017
x
=
II membro
Matematizzazione di semplici situazioni
problematiche ( M.P.)
x
9
La bilancia e il secondo principio
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
10
Cambiamento di segno
(conseguenza del Secondo principio di equivalenza)
Cambiando segno a tutti i termini di
un'equazione si ottiene un'equazione
equivalente a quella di partenza.
-2x-12
=
6-x
Equivalente a
2x+12
05/06/2017
=
-6+x
Matematizzazione di semplici situazioni
problematiche ( M.P.)
11
Forma normale di un'equazione di primo grado
Usando i principi di equivalenza, un’equazione che si
presenta in forma complessa, si può trasformare in
un’equazione equivalente di forma più semplice. La
forma più semplice in cui si può trasformare
un’equazione di primo grado è un eguaglianza tra due
monomi del tipo ax = b, detta di forma normale.
La lettera a si dice coefficiente dell'incognita, la lettera
b si dice termine noto.
Per esempio, sono nella forma normale le seguenti
equazioni
3x=2
5x=-6
-x=3
x=5
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
12
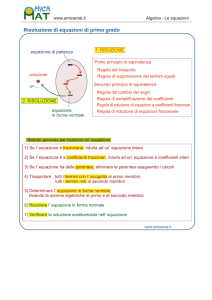
Trasformazione di un'equazione di primo grado nella forma normale
Per trasformare un'equazione di primo grado nella forma normale si trasportano al
primo membro tutti i termini con l'incognita cambiandone il segno e si
trasportano al secondo membro tutti i termini senza incognita cambiandone il
segno.
Elenco delle operazioni necessarie per risolvere un’equazione che presenta
coefficienti frazionari:
1. Trovare il m.c.m. tra i denominatori delle frazioni che compaiono nell’equazione
2. Ridurre tutti i termini allo stesso denominatore
3. Eliminare il denominatore comune moltiplicando entrambe i membri per il
m.c.m.(secondo principio)
4. Effettuare i calcoli nel primo e nel secondo membro .
5. Trasportare al primo membro tutti i termini con l'incognita cambiandone il
segno e trasportare tutti i termini senza incognita al secondo membro
cambiandone il segno. (principio del trasporto)
6. Eseguire i calcoli riducendo l’equazione nella forma normale
7. Dividere entrambe i membri per il coefficiente dell’incognita
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
13
Procedimento per la risoluzione e la verifica di un’equazione con coefficienti frazionari.
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
14
Equazioni determinate
Un'equazione si dice determinata se ammette un
numero finito di soluzioni; se l’equazione è di
primo grado si dice determinata se ammette una
sola soluzione.
• Un'equazione di primo grado che ridotta a forma
normale si presenta nella forma ax=b, con a≠0 è
sempre determinata e ammette una soluzione.
3x+2=-5x+1
portiamo i termini con la x al primo membro e quelli senza x
al secondo membro
3x+5x=1-2
sommiamo i termini simili
8x=-1 dividiamo primo e secondo membro per 8
Si ottienex=-1/8
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
15
Equazioni impossibili
Un'equazione si dice impossibile se non ammette
soluzioni.
• Un'equazione di primo grado che ridotta a forma
normale si presenta nella forma 0x=b, con b≠0 è
impossibile perché non ha soluzioni.
5x+2-3x=2x+1
portiamo i termini con la x a primo membro e quelli
senza x al secondo membro
5x-3x-2x=1-2
sommiamo i termini simili
0x=-1
0=-1
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
16
Equazioni indeterminate
Un'equazione si dice indeterminata se ammette un
numero infinito di soluzioni; cioè un'equazione si dice
indeterminata se è verificata per qualsiasi valore della
variabile e in questo senso non determina una
soluzione specifica, qualsiasi soluzione va bene.
Un'equazione di primo grado che ridotta a forma
normale si presenta nella forma 0x=0 è
indeterminata, precisamente è una identità.
7x-3+2x=12x-3-3xportiamo i termini con la x al primo membro e quelli senza x
al secondo membro
7x+2x-12x+3x=-3+3
sommiamo i termini simili
0x=0
0=0
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
17
Discussione di un’equazione di primo grado
a ≠0
x=b/a
Equazione determinata
b=0
Equazione indeterminata
b ≠0
Equazione impossibile
ax=b
a=0
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
18
Verifica della soluzione di un’equazione
Dopo aver risolto un'equazione è utile
controllare se la soluzione trovata con i
procedimenti descritti sopra è effettivamente
soluzione dell'equazione. Per fare questa
verifica, occorre sostituire all'incognita il
valore trovato ed effettuare i calcoli: se i due
membri dell'equazione sono uguali, la
soluzione trovata è una soluzione effettiva
dell'equazione
05/06/2017
Matematizzazione di semplici situazioni
problematiche ( M.P.)
19