Massimo Comun Divisore

Massimo Comun Divisore
MCD
Numeri primi e numeri composti
Nella tabella accanto trovi
indicati i divisori dei primi
tredici numeri naturali. Prova a
ricostruirla sul tuo quaderno e
proseguila almeno fino al
numero 20.
Numeri primi e numeri composti
Osserva i risultati della
tabella. Quanti risultati ha
ogni numero?
Dirai che il numero dei divisori
varia da numero a numero;
che vi è un numero particolare,
l’unità (1), che ha un solo
divisore mentre fa parte dei
divisori di ogni altro numero;
Numeri primi e numeri composti
che vi sono numeri come 2, 3,
5, 7, 11, 13, … che hanno solo
due divisori;
che i rimanenti numeri hanno
più di due divisori.
I numeri che hanno due soli
divisori, per questa loro
caratteristica, vengono
chiamati numeri primi.
I numeri che hanno più di due
divisori sono chiamati numeri
composti.
Massimo Comun Divisore
Alfredo è il cuoco del ristorante “La
Pergola”, famoso in tutta la città
per le sue ricette prelibate.
Giovedì sera aveva preparato 12
polpette e 18 patate al forno.
Massimo Comun Divisore
Volendo servire piatti contenenti lo
stesso numero di polpette e patate
quanti ne potrà preparare?
Qual è il numero massimo di piatti
tutti uguali che potrà servire in
tavola?
Massimo Comun Divisore
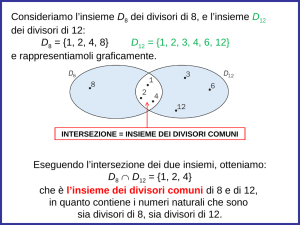
Nel disegno sottostante sono riportati tutti i divisori del
numero 12 e tutti i divisori del numero 18.
Il numero di divisori
del numero 12 e il
numero di divisori di
18 sono insiemi finiti
o infiniti?
Puoi dire lo stesso
per qualsiasi
numero?
Massimo Comun Divisore
Nel disegno sottostante sono riportati tutti i divisori del
numero 12 e tutti i divisori del numero 18.
I numeri 12 e 18
hanno divisori in
comune? Sapresti
dire quali sono?
Massimo Comun Divisore
Qual è il più grande dei divisori comuni?
Massimo Comun Divisore
Il più grande divisore comune di due numeri si
chiama massimo comun divisore. Per semplicità
si abbrevia con le iniziali maiuscole: MCD.
Così dirai che il «massimo comun divisore
fra 12 e 18 è 6» e scriverai:
MCD (12, 18) = 6
Massimo Comun Divisore
Giovedì sera Alfredo potrà
preparare 6 piatti tutti
uguali, contenenti ciascuno
2 polpette e 3 patate.
Massimo Comun Divisore
Ricopia sul tuo quaderno lo
schema grafico precedente.
Questo schema grafico ti
presenta tre insiemi di
numeri.
Indica con A l’insieme dei numeri della prima colonna:
A = {divisori di 12} = {1, 2, 3, .…, …., …. }
Massimo Comun Divisore
Ricopia sul tuo quaderno lo
schema grafico precedente.
Questo schema grafico ti
presenta tre insiemi di
numeri.
Indica con B l’insieme dei numeri della terza colonna:
B = {divisori di 18} = {…., …., …., …., …., …. }
Massimo Comun Divisore
Ricopia sul tuo quaderno lo
schema grafico precedente.
Questo schema grafico ti
presenta tre insiemi di
numeri.
Indica con C l’insieme dei numeri della colonna centrale:
C = {divisori comuni a 12 e 18} = {…., …., …., …. }
Massimo Comun Divisore
Volendo rappresentare i tre insiemi A, B e C con un
diagramma di Venn quale grafico otterrai?
Massimo Comun Divisore
L’insieme C è l’insieme intersezione degli insiemi A e B,
quali elementi contiene? Qual è il MCD di 12 e 18?
C = A B = {1, 2, 3, 6}
Massimo Comun Divisore
Vogliamo ora trovare il MCD di 20 e 30.
Procedi nel seguente modo:
(a) Trova i divisori di 20
- A ={divisori di 20} = {1, 2, 4, …, …., …. }
(b) Trova i divisori di 30
- B ={divisori di 30} = {1, 2, 3, …, …., …., …., …. }
(c) Individua i divisori comuni ad A e B
- C = {divisori comuni a 20 e 30} = {…., …., …., …. }
(d) Indica l’elemento dell’insieme C che è il MCD (20,30)
Massimo Comun Divisore
La situazione precedente si può rappresentare con un
diagramma di Venn?
MCD (20,30) = 10
Massimo Comun Divisore
Ora che hai capito il procedimento che attraverso lo
schema grafico o i diagrammi di Venn ti ha condotto ad
individuare il MCD di due numeri, puoi anche procedere
senza ricorrere ai grafici.
Sul quaderno trova il MCD (12, 15):
Div. 12 = { ………………………….}
Div. 15 = { ………………………….}
Div. Comuni a 12 e 15 = { ………………………….}
MCD (12, 15) = …………………..
Massimo Comun Divisore
Ora che hai capito il procedimento che attraverso lo
schema grafico o i diagrammi di Venn ti ha condotto ad
individuare il MCD di due numeri, puoi anche procedere
senza ricorrere ai grafici.
Sul quaderno trova il MCD (24, 25):
Div. 24 = { ………………………….}
Div. 25 = { ………………………….}
Div. Comuni a 24 e 25 = { ………………………….}
MCD (24, 25) = …………………..
Massimo Comun Divisore
Nell’ultimo degli esempi precedenti ti sei trovato
davanti due numeri che hanno un solo divisore in
comune: 1.
Quando due o più numeri hanno come MCD l’unità (1,) si
dice che sono primi tra loro.
MCD (24, 25) = 1
I numeri 24 e 25 sono primi tra loro!
Massimo Comun Divisore
Sai giudicare a vista quale delle seguenti coppie di
numeri è formata da numeri primi tra loro ?
(2, 3)
(4, 6)
(5, 6)
(7, 8)
(8, 10)
(9, 12)
(9, 14)
(5, 12)
Massimo Comun Divisore
Verifica a vista che il MCD dei numeri di ciascuna delle
seguenti coppie è 1.
(3, 4)
(8, 9)
(11, 12)
(6, 13)
(20, 21)
(19, 23)
(19, 25)
(7, 13)
Massimo Comun Divisore
Sul quaderno trova il MCD (12, 24):
Div. 12 = { ………………………….}
Div. 24 = { ………………………….}
Div. Comuni a 12 e 24 = { ………………………….}
MCD (12, 24) = …………………..
Cosa osservi? Puoi dire che tutti i divisori di 12
sono anche divisori di 24? Sai dire perché
questo avviene?
Massimo Comun Divisore
Sul quaderno trova il MCD (12, 24):
Div. 12 = { ………………………….}
Div. 24 = { ………………………….}
Div. Comuni a 12 e 24 = { ………………………….}
MCD (12, 24) = …………………..
Ogni volta che uno dei due numeri assegnati è
divisore dell’altro allora il MCD dei due numeri
è il più piccolo dei due numeri.
Massimo Comun Divisore
Sai giudicare a vista quale delle seguenti coppie di
numeri è formata da numeri di cui uno è divisore
dell’altro?
(2, 4)
(15, 9)
(3, 6)
(18, 9)
(6, 10)
(5, 7)
(12, 4)
(6, 24)
Massimo Comun Divisore
Trova a vista il MCD dei numeri di ciascuna delle
seguenti coppie.
(4, 8)
(15, 45)
(14, 7)
(36, 12)
(20, 5)
(18, 6)
(12, 4)
(77, 11)
Massimo Comun Divisore
Quando i numeri sono un po’ più grandi di quelli che
abbiamo visto finora, trovare il MCD non è molto
agevole con i metodi finora visti,
conviene allora ricorrere alla
scomposizione dei numeri in
fattori primi con il metodo
dei grafi ad albero.
Vediamo come si procede.
Massimo Comun Divisore
Vogliamo trovare il MCD (24, 36):
Scomponiamo 24 in fattori primi:
24
12
2
6
3
2
2
24 = 23 x 3
Massimo Comun Divisore
Vogliamo trovare il MCD (24, 36):
Scomponiamo 36 in fattori primi:
36
18
2
9
3
2
3
36 = 22 x 32
Massimo Comun Divisore
Il risultato delle scomposizioni è:
24 = 2x2x2x3 = 23x3
36 = 2x2x3x3 = 22 x 32
Puoi dire che i divisori primi in comune a 24
e 36 sono: ………………………………………
2, 2, 3
Allora il MCD (24, 36) = 2x2x3 = 22 x 3 = 12
Massimo Comun Divisore
Quando i numeri sono ancora più grandi di quelli che
abbiamo visto finora, conviene allora ricorrere alla
fattorizzazione.
Vediamo come si procede:
Vogliamo trovare il MCD (42, 70):
Scomponiamo 42 in un prodotto
di fattori primi:
42 = 2x3x7
Massimo Comun Divisore
Quando i numeri sono ancora più grandi di quelli che
abbiamo visto finora, conviene allora ricorrere alla
fattorizzazione.
Vediamo come si procede:
Vogliamo trovare il MCD (42, 70):
Scomponiamo 70 in un prodotto
di fattori primi:
70 = 2x5x7
Massimo Comun Divisore
Il risultato delle fattorizzazioni è:
42 = 2x3x7
70 = 2x5x7
Puoi dire che i divisori primi in comune a 42
e 70 sono: ………………………………………
2, 7
Allora il MCD (42, 70) = 2x7 = 14
Massimo Comun Divisore
Questo procedimento per
trovare il MCD di due numeri
sfrutta la possibilità di
fattorizzare un numero, per
questo si chiama metodo dei
fattori.
Massimo Comun Divisore
In pratica, il procedimento per
trovare il MCD di due numeri
con il metodo dei fattori si
trova come segue:
Si fattorizzano i due numeri
Si scelgono i fattori comuni (col
più piccolo esponente)
Si moltiplicano i fattori comuni
scelti.
Massimo Comun Divisore
Lavorando sul tuo quaderno,
trova il MCD delle seguenti
coppie di numeri col metodo dei
fattori:
(18, 24)
(40, 60)
(28, 42)
(120, 160) (36, 72)
(48, 54)
Fine