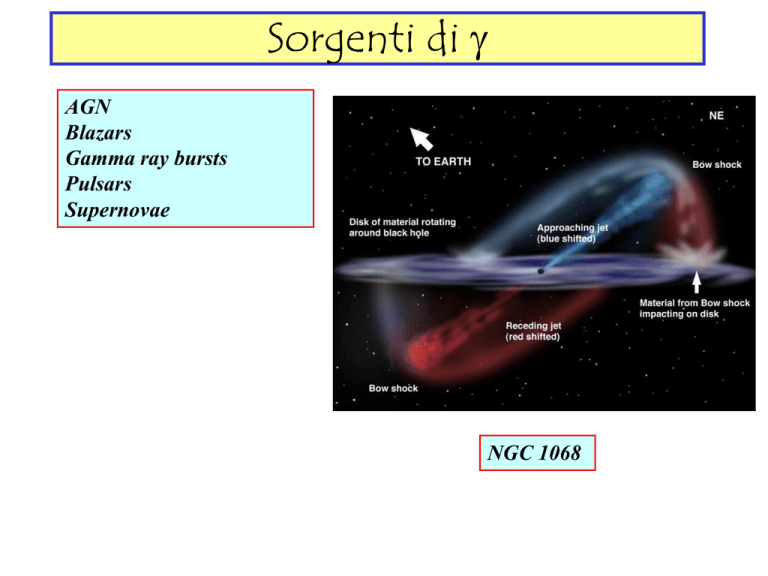
Sorgenti di g
AGN
Blazars
Gamma ray bursts
Pulsars
Supernovae
NGC 1068
Supernovae nella nostra galassia
Supernovae con “record storici”
SN del 1006
SN del 1054 CRAB Nebula.
Registrata dagli astronomi cinesi: “guest star”
SN del 1572 Supernova di Tycho
SN del 1604 Supernova di Keplero
Supernovae non viste
Cassiopaeia Supenova remnant Cassiopaeia A (~ 250 anni fa)
Oscurata dalla polvere galattica e troppo debole anche se “vicina” (2.8 kpc)
Supernovae viste in galassie vicine
SN 1987A nelle nubi di Magellano (distanza 50 kpc)
Supernova di tipo II
Supernovae
Tipi di Supernovae
Supernovae con di tipo I
Magnitudo apparente
Proprieta’ singolarmente simili per le diverse supenovae di tipo I:
-Curve di luce (andamento temporale dell’emissione) identiche
-Assenza, negli spettri ottici, delle righe dell’idrogeno
-Righe di emissione alquanto larghe
allargamento Doppler con v ~ 1000-3000 km/s
-Luminosita’ assolute identiche
Decadimento esponenziale
Tempo di decadimento ~ 70 giorni
0.5
Tempo (anni)
1
Supernovae di tipo I
Possibile modello
Collasso di una nana bianca che assorbe materia da una stella “compagna” in un
sistema binario.
Quando la massa raggiunge la massa critica per una nana bianca, si ha il collasso
formazione di una stella di neutroni e liberazione di circa 10 46 Joule.
Massa: quella tipica per una nana bianca al limite della stabilita’
Cio’ spiega le proprieta’ simili
Supernovae di tipo II
Proprieta differenziate tra SN diverse
Variazione di luminosita’ irregolare
Presenza di righe dell’idrogeno
Righe molto allargate (Doppler) v ~ 7000 km/s
Collasso di una stella di almeno 8 Ms
Curve di luce compatibili con l’espulsione di circa 10 46 J in un guscio esterno di
“gigante rossa”
Supernovae
In tutte le SN remnants si osserva emissione di radiazione che va dalle onde
radio, all’infrarosso, al visibile, ai raggi X e g
In tutte le SN remnants e’ presente un nucleo (stella di neutroni o BH).
Spesso la stella di neutroni e’ in rapida rotazione ed emette radiazione in modo
periodico (Pulsar)
esempio: CRAB T=33.2 ms
La remnant di una SN continua ad espandersi con altissima velocita’, per
centinaia o migliaia di anni.
Supernova di Tycho del 1572
Visibile ora negli X come una nube in espansione
Emissione di fotoni dalle Supernovae
Radiazione di sincrotrone
Bremsstrahlung
Scattering Compton inverso
Esempio CRAB Nebula
La CRAB
SN di tipo I ?
Al centro della CRAB Pulsar (T=33.2 ms)
La CRAB nel visibile
La CRAB nei raggi X
La CRAB
La CRAB nell’infrarosso
La CRAB nelle onde radio
La CRAB
Le dimensioni della CRAB nel visibile sono circa l’80%
di quelle nelle onde radio. Negli X sono circa il 40% di
quelle nel visibile.
Cio’ riflette il fatto che elettroni di maggiore energia emettono
preferenzialmente negli X; quelli di minore energia nel visibile
e nelle onde radio. Gli elettroni perdono energia via via che
si muovono verso le zone esterne della SN.
E’ dalle zone piu’ interne che possiamo quindi osservare
radiazione di energia piu’ elevata.
Photon spectrum
Photon spectrum
Radiazione di sincrotrone[1]
Emissione della radiazione di sincrotrone: elettrone in campo B
Frequenza angolare :
eB
eB 1
1
eB
r
g ; con :
2.8 1010 28 GHz
2gme 2me g
g
2me
B 1T
Energia irraggiata (non relativ.) :
2
2 2
g 4e 2 a
dE e a
relativ.
(nel laboratori o)
dt 60 c 3
60 c 3
Radiazione dipolare angolo tra a e direzione di osservazio ne :
E sin Potenza/un ita' di angolo solido sin 2
Radiazione polarizzat a con E// a
a
Radiazione di sincrotrone[2]
b= angolo della tangente all’elica rispetto a B (B parallelo all’asse
dell’elica)
Moto lungo l' elica a// si annulla
v2
v
v2
a sin b ; con : R
a 2 r sin b 2 r v sin b
R
2 r
v
b
B
eB
e2 B 2 2 2
2
2
v sin b a 2 2 v sin b
2gme
g me
Energia irraggiata :
dE
g 4e 2
g 4e 2 e 2 B 2 2 2
e4 B 2 v2 2 2
2
a
v sin b
g sin b
2
2
dt 60 c 3
60 c 3 g 2 me 2
60 c me c
Riscriviam ola come :
2
2
dE
e4
v B 2 2
2
c
g sin b
2
4
dt
c
2
60 c me
0
scattering g
e-
dove :
e4
T (Sezione d' urto Thomson)
2
60 c 4 me
B2
U mag (densita' di energia magnetica)
20
2
dE
v
2 T c g 2 U mag sin 2 b
dt
c
Radiazione di sincrotrone[3]
b = angolo della tangente all’elica rispetto a B
2
b
B
dE
v
2 T c g 2 U mag sin 2 b
dt
c
Limite ultrarelat ivistico (v c) :
dE
2 T c g 2 U mag sin 2 b
dt
1
Se la distribuzi one di b e' isotropa ( Pb db sin b db )
2
2
2
dE
1
4
v
v
2 T c g 2 U mag sin 3 b db T cU mag g 2
dt
20
3
c
c
Limite nonrelativ istico (v c ; g 1) :
2
dE
v
2 T c U mag sin 2 b
dt
c
e la radiazione e' emessa alla frequenza g
eB
2me
Radiazione di sincrotrone[4]
Polarizzazione della radiazione emessa (Caso non relativ.)
- Osservando da una direzione perp. a B polarizzazione lineare (nel
piano perpendicolare a B)
Vettore accelerazione esegue moto armonico in tale piano.
Intensita’ varia sinusoidalmente alla frequenza g
-Osservando da una direzione parall. a B vettore accelerazione (// ad E)
ruota Polarizzazione circolare.
-Osservando da una direzione generica polarizzazione ellittica.
Eccentricita’ dell’ellisse dipendente da (angolo d’osservazione)
(rapporto dei semiassi dell’ellisse= cos )
Radiazione di sincrotrone[5]
Caso semirelativistico
Occorre tener conto di:
a) shift Doppler dovuto alla componente di v// proiettata sulla linea di
vista: fattore 1/[1-(v///c) cos ]
-
B = v//
Caso relativistico
b) Aberrazione relativistica radiazione non
monocromatica Somma di infiniti termini dipolari:
l=l r con (r = g/g )
Radiazione di sincrotrone[6]
Caso relativistico
b) Aberrazione relativistica radiazione non
monocromatica Somma di infiniti termini dipolari:
B = v//
l=l r con (r = g/g )
l r
(l 1,2,3....) e dE/dt funzione di l
v //
1
cos
c
v
1
Per si dimostra che :
c
l
l
dE/dt l 1 v 2
dE/dt l c
per particelle non relat. potenza per armoniche elevate
e' piccola.
Per particelle relativist iche tale potenza non e' trascurab ile & picchi si allargano
Spettro praticamen te continuo
Radiazione di sincrotrone[7]
Caso semirelativistico
v/c=0.4
g=1.1
Armoniche polarizzate
ellitticamente.
Da misure della polariz. possibile determ.
orientazione di B rispetto alla linea di vista
Esempio: AM Herculis Binaries
l=5 10-6 m. = 6 1013 Hz = 6 104 GHz = (28/g) B.
Per g=1 B = (6/28) 104 T = 2142 T
Radiazione di sincrotrone[8]
Il caso relativistico puo’ esser
trattato come il limite di quello
semirelativistico di figura
le armoniche sono molto
numerose e tendono a “fondersi”
dando uno spettro continuo.
Armoniche polarizzate ellitticamente. Se possibile misurare
la polarizzazione delle singole armoniche informazioni
dettagliate sull’intensita’ del campo B.
In alcuni casi si riesce a distinguere le singole armoniche.
Distribuzione spettrale[1]
Particella che ruota ortogonlamente
attorno a B (b=900). Radiazione di
dipolo (non relativistico)
Sistema del laboratorio:
sin
cos '
v
c
sin '
; cos
v
g 1 v cos '
1 cos '
c
c
1
e.g. per f’ = /4 intensita’ dimezzata
nel sistema di riposo
nel laboratorio: sinf ~ f ~ 1/g
Solo quando lo stretto fronte d’emissione spazza la posizione occupata
dall’osservatore apprezzabile intensita’ rivelata.
Grosso impulso di radiazione ogni volta che la velocita’ dell’elettrone giace
entro un angolo ~ 1/g rispetto alla linea di vista
Distribuzione spettrale[2]
Durata dell' impulso visto dall' osservator e molto minore di : Periodo dell' orbita/ g .
Infatti :
Radiazione dal punto A raggiunge l' osservator e al tempo : R
Radiazione dal punto B, emessa dopo un tempo : L
R L
c
v
a raggiunger e l' osservator e
c
L RL R L v
Δt
1
c c v c
v
L
Solo per c troveremm o Δt
v
Impiega un tempo
Forma alternativ a :
L rg rg
1
L
1
1
; con :
v
v
r rg
g
v gr g
Inoltre :
1 v
v
c
c
c
1-
1 v
c
1 v
1 v c
2
2
1 v c
1
(poiche' v c)
2g 2
Dt=1/(2g2g)<<1/g
Massima componente di
Fourier:
~ Dt-1 ~ g2 g
Se b # 900
= g2 g sinb
E’ anche:
~ g2 g = g2 v/(2rg) = g3 r
Distribuzione spettrale[3]
emissione collimata
2
dE 4
v 2
T cU mag g
dt 3
c
ac
g
Frequenza angolare :
eB
eB 1
1
eB
r
g ; con :
2.8 1010 28 GHz
2gme 2me g
g
2me
B 1T
Energia irraggiata (non relativ.) :
2
2 2
g 4e 2 a
dE e a
relativ.
(nel laboratori o)
dt 60 c 3
60 c 3
Radiazione dipolare angolo tra a e direzione di osservazio ne :
E sin Potenza/un ita' di angolo solido sin 2
Radiazione polarizzat a con E// a
Distribuzione spettrale[4]
Massima componente di Fourier: ~ Dt-1 ~ g2 g = g3 r = g3 v/(2rg)
Se b#900 =g2 g sinb
Per valutazioni di ordini di grandezza e’ sufficiente far uso di queste
relazioni per valutare le frequenze dominanti, e della
2
dE 4
v 2
T cU mag g
dt 3
c
per valutare l’energia irraggiata per unita’ di tempo
Per calcoli piu’ dettagliati e’ necessario ricorrere ad una procedura
di maggiore complessita’, partendo dai potenziali di Lienard-Weickert
Distribuzione spettrale[5]
2
La perdita d’energia e’ ancora data da:
dE 4
v 2
T cU mag g
dt 3
c
La distribuzione spettrale e’:
3 e 3 B sin β
J
F
x
;
dove
:
x
8 2 0 cme
c
3cg 3
e dove la frequenza critica c
; con a il raggio dell ' elica descritta dall ' elettrone
2a
La funzione F ( x) e': F ( x) x K 5 z dz
x
3
e K 5 z la funzione di Bessel modificata di ordine 5 / 3
3
c 3cg 3
v
3cg 3r sin b 3 c g 3r sin b
Notiamo che c
con: a
c
2 4a
r sin b
4 v
2v
2
Al limite per v c, questa diventa:
3 g 3r sin b 3 3
3
g r sin b ; con r g / g c g 2 g sin b , molto simile al valo re: g 2 g
2
2
2
2
corrispond ente alla frequenza che caratterizza il massimo dell'emissio ne.
Distribuzione spettrale[6]
x
F(x)
1.0 10-4
0.0996
1.0 10-3
0.213
1.0 10-2
0.445
3.0 10-2
0.613
1.0 10-1
0.818
2.0 10-1
0.904
2.8 10-1
0.918
3.0 10-1
0.918
5.0 10-1
0.872
8.0 10-1
0.742
1
0.655
2
0.301
3
0.130
5
2.14 10-2
10
1.92 10-4
Distribuzione spettrale[7]
Spettro caratterizzato da un ampio massimo:
centrato all’incirca alla frequenza c
con:
D/ ~ 1
Massimo in realta’ alla frequenza:
max = 0.29 c
con:
c = 3/2 g2 g sinb
x=/c
Distribuzione spettrale[8]
Andamenti asintotici della distribuzione spettrale (1)
Andamenti asintotici della distribuzione spettrale (2)
Andamenti asintotici della distribuzione spettrale (3)
Radiazione di sincrotrone da elettroni con
distribuzione spettrale ~E-p
J
3e Bk sin me c
2
8 0 cme p 1 3eB sin
3 4
3
Integrando su
Cioe' va' come :
B
Se
p 1
2
p 2
p 1
2
p 19 p 19
4 12 4 12
(distribuit o isotropica mente) :
me 3c 4
3e3 Bk
J
2
16 0 cme p 1 3eB
p 1
2
p 1
0.5
2
p 1
2
p 19 p 19 p 5
4 12 4 12 4 4
p 7
4 4
Radiazione di sincrotrone da elettroni con
distribuzione spettrale ~E-p
Derivazion e approssima ta del risultato
Spettro di fotoni emessi da elettroni di energia E concentrat o attorno alla frequenza critica :
2
E
eB
g; g
c g g
2
2 me
mec
Ammettiamo che TUTTI i fotoni siano emessi a questa frequenza Energia irraggiata nel range d attribuibi le ad elettroni
nel corrispond ente range E E dE :
2
dE
J d N E dE
;
dt
E γme c 2
g
(*)
con :
k E-p = k (me c2)-p (/g)-p/2
1
2
me c 2 ;
2
dE
me c 2
2 g
1
1
2
d
2
2
E B
E B
4
dE 4
; sostituiam o nella (*) : J T c
T c
2
2
3
dt 3
m ec 20
m e c 20
2 12 12
B g
g
g
2
p
2
; con B g
; J
p 1
( p 1)
2
B
2
2
me c
2 g
2
1
2
1
2
k
g
p
2
m c
2 p
e
Autoassorbimento
Occorre tener conto dell’autoassorbimento della
radiazione di sincrotrone.
Gli stessi fotoni emessi per rad. di sincrotrone possono
esser riassorbiti dagli elettroni attraverso il processo
inverso. Cio’ e’ importante sopratutto a basse frequenze
e porta ad una deformazione dello spettro che, a basse
frequenze, andra’ come 5/2.
Polarizzazione della radiazione[1]
La radiazione e’ confinata entro l’angolo
solido .
Una caratteristica distintiva della radiazione
di sincrotrone e’ l’elevato grado di polarizzazione
lineare.
Ad esempio, una polarizzazione lineare di 80%
(con un errore del 20%) e’ stata osservata nel
g-ray burst del 6 Dicembre 2002 (GRB021206)
facendo uso del rivelatore RHESSI nella zona
di energie dei g tra 25 KeV e 2 MeV.
E’ anche presente polarizzazione circolare, ma la
sua intensita’ e’ circa 1/g di quella lineare.
Polarizzazione della radiazione[2]
Polarizzazione della radiazione[3]
Polarizzazione della radiazione[4]
Polarizzazione della radiazione[5]
Polarizzazione della radiazione[6]
Polarizzazione della radiazione[7]
Polarizzazione della radiazione[8]
Polarizzazione della radiazione[9]
Polarizzazione della radiazione[10]
Radiazione di sincrotrone
Espessioni numeriche utili[1]
Perdita d' energia :
2
dE
v
- 2 T cU magg 2 sin 2 b
dt
c
Mediata su b :
dE
v
- 1.058 10 14 B 2g 2
dt
c
In GeV/s, con v c :
2
2
2
1.587 10
14
v
B g sin 2 b
c
2
2
W con B in T
2
dE
B E
- 3.79 10 6
Gev / s
dt
Gauss
GeV
Spettro d' emissione di un singolo elettrone :
con B in T
3e3 B sin b
J
F 2.344 10 25 B sin b F
40 cme
c
c
3
eB
c g 2
4.199 1010 g 2 B Hz
2 2me
W Hz
2
E B
In GeV : c 1.6110
Hz
GeV Gauss
Lo spettro in numero di fotoni ha un picco a 0.29 c .
13
Per E 10 GeV e B 1G c 1.61 GHz [l 0.186 m]
Per E 105 GeV e B 1G c 1.611017 Hz [l 1.86 nm];
Per E 105 GeV e B 1T c 1.6110 27 Hz [l 2.07 10 19 m]
W con B in T
Radiazione di sincrotrone
Espessioni numeriche utili[2]
Spettro di radiazione da elettroni con distribuzi one di potenza di esponente - p :
J
3e Bk 3eB
3 4
40 cme 2me c
3
p 1
2
a p ; con :
p 19 p 1 p 5
4 12 4 12 4 4
a p
2
p 1 p 7
4 4
1.253 10
In unita' SI J 2.344 10 25 a p B p 1/ 2 k
37
p 1
2
Wm
3
Hz 1
Scattering Compton inverso (IC)
g
Scattering di un elettrone di alta energia con fotoni ambiente di energia h 0 .
N numero di fotoni per unita' di volume densita' di energia dei fotoni : U rad Nh 0
e
Energia massima che un fotone puo' acquistare in una collisione con un elettrone
di alta energia (collision e frontale) h max
g
2
v
h 0g 1 4g 2 h 0
c
2
e
(v e g sono relativi all' elettrone)
v2 2
dE 4
Perdita d' energia dell' elettrone :
T cU rad 2 g
dt 3
c
v c
4
T cU radg 2
3
3 T c N 0
2
2
Spettro della radiazione diffusa : I d
2 ln 2 4g 0 2 d
16g 2 0 2
2g 0
4g 0
N 0 densita ' numerica di fotoni
4
Energia media dei fotoni diffusi : g 2 h 0
3
Frequenze tipiche dei fotoni prodotti (per g 103 10 4 ) :
Per scattering sui fotoni della radiazione di fondo ( 0 1011 Hz ) 106 1011 Hz 1017 Hz (0.4 KeV raggi X )
Per scattering sui fotoni ottici ( 0 1015 Hz ) 106 1015 Hz 10 21 Hz (4 MeV raggi g )
Scattering Compton inverso (IC)
Perdite d’energia per IC e Sync. Rad.
Perdita d' energia di un elettrone per radiazione di sincrotron e (v c) :
2
dE
2 v
2
-
2 T cU mag g sin b
dt
c
9.9 10 4 g 2 B
2
1.587 10 14 g 2 B 2 sin 2 b
W con B in T
eV s
1
Mediata su b :
dE
-
6.6 10 4 B 2 g 2
dt Rad . Sinc.
eV s
1
con B in T
IC :
4
dE
2
-
T cU rad g
dt IC 3
Espression i molto simili; U mag U rad
Perdita d'energia di pende dal campo elettrico che accelera l 'elettrone, visto nel sistema di quiete di questo;
e' irrilev ante che il campo sia quello v B dovuto al moto nel campo magnetico o quello a ssociato a i fotoni
che incont ra.
Perdite d’energia per IC e Sync. Rad.
dE
Inoltre :
dt IC
U rad
dE
dt Rad. Sinc. U mag
Valori tipici : B 3 10 -10 T ; U rad 6 10 5
eV m 3 U rad U mag 3
Massimo tempo di " vita" di un elettrone di alta energia nell' Universo :
E
E
E
2.3 1012
anni
dE dt IC 4 cU g 2 4 cU g 2
g
T
rad
T
CBR
3
3
Per U CBR 2.62 10 5 eV m 3 . Per un elettrone di 100 GeV 10 7 anni
Spettro di una Blazar
(Radio) Pulsars
Scoperte nel 1967 da Hewish e Bell
Predette nel attorno al 1934 da Baade
e Zwicky come “stelle di neutroni”
Predizione non prevedeva emissione
“non termica”
Successiva predizione nel 1967 di
Pacini: stelle di neutroni magnetizzate
e ruotanti emissione radio
Pulsars (1)
Impulsi rivelati quando uno dei
jets punta verso la Terra
Elettroni che spiralizzano nel campo
magnetico della stella di neutroni
Pulsars (2)
Periodi di rotazione P=(0.0015-4.0) s
Modello: NS con momento magnetico non allineato con l’asse di
rotazione
emissione di dipolo magnetico
Periodo P; frequenza angolare W=1/P.
1
P
Q 1012 1019 ; tra gli orologi piu' stabili dell' Universo !
ΔΩ TΩ TP
T
T periodo di osservazio ne :
Ω
Ω
P QP
T
108 1011
P
Fattore di qualita' : Q
Potenza totale irraggiata da un dipolo magnetico ruotante con veloci ta' angolare W :
p 2
0
dE
;
dt 6 c 3
Per un dipolo che ruoti ad un angolo rispetto all' asse
componente del momento perpendico lare all' asse di rotazione :
p p0 sin Wt
2
0 d 2
0
dE
2
p
sin
W
t
p0 W 4
0
3
2
3
dt
6 c dt
6 c
Pulsars (3)
La potenza irraggiata e' estratta dall' energia cinetica di rotazione
1 2
IΩ
2
4 2
μ
Ω
p0
d 1 2
dE
0
IΩ IΩΩ
; da cui :
3
dt 2
dt
6
π
c
2
3
μ
p
Ω
0
0
Ω
Ω3
3
6π c I
" Braking index" n definito da : Ω -K Ω n
Nel nostro caso quindi n 3
: Ω -K Ω n
Misura di n possibile se si misura Ω
dividendo membro a membro :
n Ω n 1 Ω
Ω ν ν
Ω
Ω
n 2 2
n
Ω
Ω
Ω
ν
1
2 P 2 P
Periodo : P ; 2 P; 3 2
P
P
P
PP
n2
P 2
1
n K Ω n 1 Ω
Ω
Misure di n:
CRAB: 2.515 +/- 0.005
PSR 1509-58: 2.8 +/- 0.2
PSR 0540-69: 2.01 +/- 0.02
Eta’ di una Pulsar (1)
L’eta’ puo’ esser stimata ammettendo che la decelerazione sia
caratterizzata da un “braking index” costante
Ω KΩ n ; Integrando :
τ
Ω
Ω
dΩ
1 1
1
0 Ω n dt K τ; Ω Ω n K τ; n 1 Ω0n1 Ω n1 K τ
0
Ω (n1 )
Ω (n1 )Ω n
Ω
Se n 1 e Ω0 Ω τ
K(n 1 ) K(n 1 )Ω n
(n 1 )Ω
P
;
(n 1 )P
Per n 3 τ
P
2 P
Eta’ di una Pulsar (2)
Dal grafic o di P in funzio ne di P si vede che
la vita media per la grande maggioranza delle
pulsar e' dell'ordin e di 107 anni.
Crab Pulsar: τ 1400 anni
Crab Nebula (Supernova): esplosa nel 1054
La CRAB
(La “candela Standard”)
1) Prima sorgente g chiaramente evidenziata (Whipple 1989)
2) Pulsar (Plerion) vista dagli astronomi cinesi nel 1054
3) Lo spettro è spiegato dal modello Synchrotron Self-Compton
(SSC) di DeJager Harding (1992)
4) Rilevata da almeno 9 telescopi con qualche inconsistenza in
spettro ed intensità (Tibet As, CAT)
5) Forma dello spettro e flusso permettono di calcolare il campo
magnetico medio attorno alla nebula
6) Misurati gamma fino a 50 TeV
La CRAB Nebula
Supernova remnant e pulsar
Stella di neutroni in rapida rotazione, circondata da una nebula luminosa,
diffusa
Dimensione della Nebula: 6 anni-luce; in espansione ad una velocita’ di
~ 1.8 Milioni di km/ora
Radiazione di sincrotrone
Misure effettuate nelle onde radio, nell’infrarosso, nell’ottico,
negli X, nei g.
Periodicita’ (T=33 ms) rivelata a tutte le lunghezze d’onda, fino a circa 10
GeV (Egret). Non a energie delle centinaia di GeV o del TeV.
Spettro caratterizzato da un indice g pari a circa (2.5-2.7)
CAT (325 GeV-8 TeV)
Whipple (300 GeV-10 TeV)
Hegra(1 TeV-10 TeV)
CANGAROO (7 TeV-50 TeV)
g=-2.57+/- 0.14
g=-2.49+/-0.06
g=-2.71+/-0.17
g=-2.53+/-0.15
La CRAB Nebula
Limiti superiori sullo spettro
“pulsato” ottenuti da Whipple
confrontati con i dati di Egret
Unita’ “CRAB”
Unita’ di intensita’ degli X, valutata a 5.2 KeV (o nella banda:2-11 KeV).
Se una sorgente ha il medesimo tipo di spettro della CRAB in tale banda
allora e’ possibile confrontarne la luminosita’ con quella della CRAB ed
esprimerla in “CRAB units”.
Numericamente: 1 CRAB=1060 microJansky, ed
1 microJansky = 0.242x10-11 ergs cm-2 sec-1 KeV-1
= 1.51x10-3 KeV cm-2 sec-1 KeV-1
Esempio: la stella Algol produce, tra 2-11 KeV, 9 microJansky o:
9/1060=0.0085 Crabs
Analoga convenzione e’ adoperata nella zona dei gamma
Andamento temporale delle sorgenti osservate