ITGC Achille Mapelli, Monza
RETTE PARALLELE
&
APPLICAZIONE SUI TRIANGOLI
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
INTRODUZIONE.
DEFINIZIONE BISETTRICE DI UN ANGOLO
Si chiama bisettrice di un angolo di vertice O la semiretta di origine O,
interna all’angolo, che divide l’angolo in due parti congruenti.
È detta retta bisettrice di un angolo la retta che contiene la semiretta
bisettrice e quindi anche la sua opposta,
bisettrice de secondo angolo avente gli sessi lati del primo.
DEFINIZIONE MEDIANA IN UN TRIANGOLO
In un triangolo, la mediana è il segmento che unisce un vertice
con il punto medio del lato opposto. Il triangolo viene diviso
dalla mediana in due triangoli aventi la stessa superficie e tutte le altre rette che dividono
il triangolo in due parti di ugual superficie che
passano per il baricentro.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
TEOREMI FONDAMENTALI SULLE RETTE PARALLELE
CAPITOLO 1: Rette Tagliate Da Una Trasversale.
Due rette di un piano che intersecano una terza retta, detta trasversale, formano otto angoli che hanno nomi
particolari.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
Per semplicità, indichiamo questi
angoli con i numeri da 1 a 8, come in
figura
2 e 8 o 3 e 5 sono alterni interni
4 e 6 o 1 e 7 sono alterni estreni
1 e 5;2 e 6; 4 e 8; 3 e 7 sono corrispondenti
2 e 5 o 3 e 8 sono coniugati interni
1 e 6 o 4 e 7 sono conigati esterni
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
Possiamo dimostrare che se uno dei seguenti
enunciati è vero, lo sono anche gli altri:
A gli angoli alterni interni sono congruenti;
B gli angoli alterni esterni sono congruenti;
C gli angoli corrispondenti sono congruenti;
D gli angoli coniugati sono supplementari.
Possiamo così formulare quattro teoremi ognuno dei quali
ha per tesi uno dei quattro enunciati e per ipotesi gli altri tre.
Cominciamo a considerare il primo dei quattro teoremi: supponiamo che sia vero l’enunciato A e
dimostriamo che sono veri anche gli enunciati B, C, D.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
TEOREMA 1
Se due rette, tagliate da una trasversale, formano una coppia di angoli alterni interni congruenti, allora gli
angoli alterni esterni sono congruenti, gli angoli corrispondenti sono congruenti, gli angoli coniugati sono
supplementari.
Ipotesi: 2≈8
Tesi: 4 ≈ 6, 1 ≈ 7, 2 ≈ 6, 4 ≈ 8…, 3+8 ≈ angolo piatto, …
Consideriamo la FIGURA, cominciamo a rilevare che sono
Congruenti anche gli altri angoli alterni 3 e 5 perché adiacenti
(e quindi supplementari) ad angoli congruenti. Possiamo
così considerare che per ipotesi si abbia l’enunciato A .
Sempre osservando la FIGURA 2, abbiamo 4 ≈ 2 e 6 ≈ 8,
perché angoli opposti al vertice e quindi, poiché per
ipotesi 2 ≈ 8, per proprietà transitiva della congruenza
deduciamo che 4 ≈ 6. Analogamente si dimostra che 1 ≈ 7.
Resta così dimostrato che gli angoli alterni esterni sono anch’essi congruenti: l’enunciato B è vero.
Osserviamo ora che, essendo 2 ≈ 8 per ipo e 6 ≈ 8 perché opposti al vertice, per la proprietà transitiva è anche
2 ≈ 6. Analogamente si dimostra la congruenza delle altre tre coppie di angoli corrispondenti e resta così
dimostrato che è vero l’enunciato C.
Consideriamo ora gli angoli 3 e 2 che sono adiacenti: pertanto 3 è supplementare di 2 e, per ipo, è 2 ≈ 8, quindi
l’angolo 3 risulta supplementare anche dell’angolo 8, a esso coniugato. Analogamente si dimostra che le altre
coppie di angoli coniugati sono angoli supplementari: quindi anche l’enunciato D è vero. C.v.d.
Analogamente si dimostrano gli altri enunciati.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
TEOREMI FONDAMENTALI SULLE RETTE PARALLELE
CAPITOLO 2: Esistenza Delle Rette Parallele.
Sappiamo che due rette di uno stesso piano che non hanno alcun punto in comune sono dette
parallele.
Per indicare che due rette a e b sono parallele si scrive a // b.
L’esistenza di rette parallele risulta dal seguente teorema.
TEOREMA 2
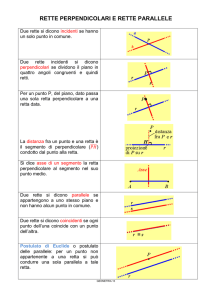
Due rette di un piano perpendicolari a una stessa retta non hanno alcun punto in comune, cioè sono parallele tra loro.
Ipotesi: a ┴ c e b ┴ c
Tesi: a//b
Siano a e b due rette perpendicolari ala stessa retta
c rispettivamente nei punti A e B (FIGURA 3);
Vogliamo dimostrare che sue rette non possono incontrarsi in un punto O.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
Dimostreremo per assurdo: supponiamo che le rette
non siano parallele, cioè che si incontrino in un punto O (come
In figura).
In tal caso, si formerebbe il triangolo ABO nel quale si avrebbe due
angoli retti (OAB deve essere retto perché formano delle rette
perpendicolari a e c, OBA deve essere anch’esso retto perché
formano delle rette perpendicolari b e c) . Siamo quindi arrivati
ad un assurdo, dato che in precedenza avevamo dimostrato che
in un triangolo non può esserci più di un angolo retto. Quindi è
assurdo aver negato che le rette a e b siano parallele e perciò
Deve essere a//b.
C.v.d.
Ora siamo in grado di costruire una retta, passante
per un punto P, parallela a una retta data. Infatti
basta condurre da P la perpendicolare s della retta
r e, sempre da P, la perpendicolare p alla retta s.
Per il TEOREMA 2, poiché r┴s e p┴s, le rette r e p
risultano parallele e quindi p è la retta richiesta.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
TEOREMI FONDAMENTALI SULLE RETTE PARALLELE
CAPITOLO 3: Il Postulato Di Euclide.
La costruzione eseguita prima, che dimostra l’esistenza della retta per P parallela alla retta r, sembra
suggerire che la retta p a cui si giunge è sempre la stessa, cioè che per il punto P si possa condurre
una sola parallela.
L’unicità della parallela non si può dimostrare in alcun modo, perciò siamo costretti ad ammetterla come
postulato; tale postulato è conosciuto come postulato delle parallele o anche postulato di Euclide.
POSTULATO 6 POSTULATO DI EUCLIDE
La parallela a una retta data, condotta per un punto esterno a essa, è unica.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
TEOREMI FONDAMENTALI SULLE RETTE PARALLELE
CAPITOLO 4: CRITERI DI PARALLELISMO.
È evidente che mediante il disegno non potremo mai definire se due rette sono parallele mediante la
definizione, perchè l’eventuale punto di intersezione di due rette tracciate su un foglio potrebbe cadere a
una distanza praticamente non raggiungibile. Per capire se due rette sono parallele bisogna ricorrere ai
seguenti criteri.
TEOREMA 3
Se due rette di un piano formano con una trasversale
1.
due angoli alterni interni (o esterni) congruenti, o
2.
due angoli corrispondenti congruenti, o
3.
due angoli coniugati supplementari,
allora le due rette sono parallele.
Osserviamo che se due rette tagliate da una trasversale formano angoli alterni esterni congruenti, o angoli
corrispondenti congruenti, o angoli coniugati supplementari, allora per il TEOREMA 1 formano anche angoli alterni
interni congruenti.
Perciò basta dimostrare che la tesi è vera nel caso che le due rette formino con la trasversale
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
Ipotesi: AEF ≈ EFD
Tesi: AB//CD
Procediamo per assurdo e supponiamo dunque che le rette AB e CD non siano parallele: se le semirette EB, FD si
incontrassero in un punto O otterremmo il triangolo OEF per il quale si avrebbe che l’angolo esterno AEF è congruente
all’angolo interno EFD. Ma ciò è impossibile perché abbiamo già dimostrato che l’angolo esterno è maggiore di ciascuno
degli angoli interni non adiacenti a esso. Dunque non è possibile l’esistenza del punto O. in modo analogo si dimostra che
non possono incontrarsi le due semirette EA e FC. Ne segue che le rette AB e CD sono parallele.
c.v.d.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
TEOREMI FONDAMENTALI SULLE RETTE PARALLELE
CAPITOLO 5: Proprietà Fondamentali Delle Rette Parallele.
TEOREMA 4
Se due rette di un piano sono parallele, esse, tagliate da una trasversale, formano:
1.
Angoli alterni interni (ed esterni) congruenti,
2.
Angoli corrispondenti congruenti,
3.
Angoli coniugati supplementari.
Osserviamo che basta dimostrare che le due rette formano, con la trasversale, angoli alterni congruenti.
Infatti, per il TEORMA 1, esse formeranno, in tal caso, anche angoli alterni esterni congruenti, angoli corrispondenti
congruenti e angoli coniugati supplementari.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
Ipotesi: AB//CD
Tesi: AEF ≈ DFE
Per assurdo supponiamo falsa la tesi, supponiamo
cioè che la retta AB formi con la trasversale HK un
angolo AEF alterno interno a DFE e non congruente a esso.
Allora esisterà una retta MN, passante per E e distinta da AB,
che formi con HK una angolo MEF congruente all’angolo EFD:
tale retta, per il TEOREMA 3, risulterà parallela a CD. Ma,
per ipotesi, AB//CD e quindi per il punto E passerebbero
due rette, la AB e la MN, entrambe parallele a CD;
questo è contro il postulato di Euclide. Pertanto la tesi non può
essere negata ed essa risulta vera: si ha AEF ≈ DFE.
c.v.d.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
TEOREMI FONDAMENTALI SULLE RETTE PARALLELE
CAPITOLO 6: Condizione Necessaria e Sufficiente Per il Parallelismo.
Quando di un teorema diretto, risulta vero anche il suo inverso, gli enunciati dei due teoremi si possono
esprimere con una sola proposizione. Perciò i TEOREMI 3 e 4 si possono riassumere nel seguente
enunciato.
TEOREMA 5
Condizione necessaria e sufficiente affinché due rette siano parallele è che esse formino con una
trasversale una coppia di angoli alterni interni (o esterni) congruenti, oppure due angoli
corrispondenti congruenti, oppure due angoli coniugati supplementari.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
TEOREMI FONDAMENTALI SULLE RETTE PARALLELE
CAPITOLO 7: Distanza Di Due Rette Parallele.
TEOREMA 6
Segmenti paralleli compresi fra rette parallele sono congruenti.
Consideriamo la figura seguente.
Ipotesi: a//b;
A Є a,BЄa, CЄb, DЄb;
AB//CD;
Tesi: AB ≈ CD
Se uniamo A con D otteniamo due triangoli ABD e ADC congruenti per il secondo criterio di congruenza: infatti essi hanno
AD in comune, BAD ≈ ADC perché alterni interni delle rette parallele AB e DC tagliate da AD, BDA ≈ DAC perché alterni
interni delle rette parallele BD e AC tagliate da AD. Poiché in triangoli congruenti a elementi congruenti si oppongono
elementi congruenti, sarà AB ≈ DC. C.v.d.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
TEOREMA 7
Se due rette sono parallele, tutti i punti dell’una sono equidistanti dall’altra.
Il teorema è la conseguenza del TEREMA 6. Esaminiamo la figura:
Ipotesi: a//b
A Є a, C Є a, B Є b, D Є b
AB ┴ b, CD ┴ b.
Tesi:
AB ≈ CD
Osserviamo per prima cosa che, perché due rette di un piano perpendicolari a una stessa retta sono parallele tra loro, è AB//CS. Infatti, per ipotesi,
sia AB sia CD sono perpendicolari alla stessa retta b. allora , il TEOREMA 6 ci assicura che AB ≈ CD. C.v.d.
Il TEREMA 7 giustifica la seguente definizione
DEFINIZIONE DISTANZA DI DUE RETTE
Si dice distanza di due rette parallele la distanza di un punto qualsiasi di una di esse dall’altra.
Quindi distanza di due rette parallele a e b è rappresentato dal segmento di esse intercettato su una qualunque
perpendicolare alla rette a e b
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
DEFINIZIONE STRISCIA DI PIANO
La parte di piano compresa tra due rette parallele si chiama striscia; le parallele sono dette lati della striscia e la
distanza di tali rette è detta altezza della striscia.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
APPLICAZIONE SUI TRIANGOLI
CAPITOLO 8: Secondo Teorema Dell’Angolo Esterno.
TEOREMA 8 SECONDO TEOREMA DELL’ANGOLO ESTERNO
In ogni triangolo un angolo esterno è congruente alla somma dei due angoli interni non adiacenti.
Sia ABC un triangolo qualsiasi e consideriamo su di esso l’angolo esterno ACD(ipotesi);la tesi è ACD ≈ BAC + ABC.
Ipotesi: ACD angolo esterno
Tesi: ACD ≈ BAC + ABC
Per la dimostrazione tracciamo dal
punto C la semiretta CE parallela al
lato AB e consideriamo i due angoli
in cui tale semiretta divide l’angolo
esterno ACD. Risulta BAC ≈ ACE
perché angoli alterni interni rispetto
alle parallele AB, CE tagliate dalla
trasversale AC; inoltre ABC ≈ ECD
perché corrispondenti rispetto alle
stesse parallele tagliate dalla
trasversale BD. Deduciamo così
che BAC + ABC ≈ ACE + ECD.
Dalla figura, vediamo che ACE + ECD = ACD
Quindi dal confronto delle due somme, per la proprietà transitiva dalla congruenza, abbiamo BAC + ABC ≈ ACD.
c.v.d.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
ITGC Achille Mapelli, Monza
APPLICAZIONE SUI TRIANGOLI
CAPITOLO 9: Proprietà Dell’Altezza Del Triangolo Isoscele.
TEOREMA 9
In un triangolo isoscele l’altezza relativa alla base è anche mediana e bisettrice dell’angolo al vertice.
Consideriamo i triangoli BHA e CHA, dove AH è l’altezza relativa alla
base BC, e osserviamo che essi hanno:
HЄBC
AB ≈ AC per ipotesi;
AH┴BC
ABH ≈ ACH perché angoli alla base di un triangolo isoscele;
AHB ≈ AHC perché entrambi retti, essendo AH ┴BC.
Quindi i due triangoli, poiché hanno congruenti un lato e due angoli,
ugualmente disposti rispetto al lato, risultano congruenti per il
secondo criterio di congruenza generalizzato.
Dalla congruenza dei triangoli ABH e ACH possiamo concludere che
BH ≈ HC
BAH ≈ HAC
Ipotesi: AB ≈ AC
AH è mediana
AH è bisettrice
c.v.d.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo
Tesi: BH ≈ HC
BAH ≈ HAC
ITGC Achille Mapelli, Monza
APPLICAZIONE SUI TRIANGOLI
CAPITOLO 10: SOMMA DEGLI ANGOLI INTERNI DI UN POLIGONO.
La seguente proprietà, relativa agli angoli di un poligono, vale qualsiasi sia il numero dei suoi lati.
TEOREMA 10
La somma degli angoli interni di un poligono convesso è congruente a tanti angoli piatti quanti sono i lati del poligono
meno due.
Dalla figura vediamo che, unendo tutti i vertici di un poligono
convesso di n lati con un punto qualunque O interno del
poligono è uguale alla differenza fra la somma degli angoli
Interni di tutti i triangoli costruiti e la somma degli angoli che hanno il vertice
In O.
La somma degli angoli interni di tutti i triangoli è uguale a n angoli piatti,
mentre la somma degli angoli interni di tutti i triangoli è uguale a n angoli
piatti.
Quindi la somma degli angoli del poligono, essendo uguale alla differenza fra la somma degli angoli di tutti i triangoli
costituiti e quella degli angoli che hanno il vertice in O, è congruente a (n – 2) angoli piatti, cioè tanti angoli piatti quanti
sono i lati del poligono meno due angoli piatti.
c.v.d.
Aprile 2011 – Classe:1^D(LS) Alunno: Sausto Matteo