• Se un triangolo rettangolo ha un angolo acuto di 30°,l’altro angolo
acuto è di 60°.
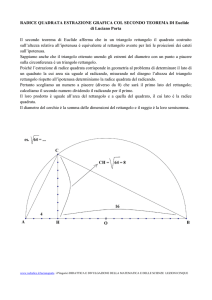
Il triangolo rettangolo ABH può essere considerato come la metà del
triangolo equilatero ABC e precisamente come uno dei due triangoli
rettangoli congruenti in cui l’altezza AH del triangolo equilatero
divide il triangolo stesso
L’ipotenusa AB è congruente al lato del triangolo equilatero,il cateto BH
è congruente alla metà del lato e l’altro cateto AH è congruente
all’altezza del triangolo equilatero.
Se l è la misura di AB ed h quella di AH abbiamo:
h=lx 3
l=2xh
3
Oppure
h=lx0,866
l= h
0,866
Perché l’altezza è uguale al lato
per radice quadrata di tre???
• Se un triangolo rettangolo ha un angolo
acuto di 30°,il cateto opposto ad esso è la
metà dell’ipotenusa,mentre l’altro
cateto,cioè quello opposto dell’angolo
60°,è congruente all’altezza del triangolo
equilatero avente per lato l’ipotenusa.
ANGOLI DI 45°
•
•
•
•
•
•
•
•
Indicando con d la misura della diagonale e con l quella del lato del quadrato ABCD
ed applicando il teorema di Pitagora ad uno dei due triangoli rettangoli isosceli
congruenti in cui esso risulta diviso dalla diagonale DB,otteniamo:
D2=l 2+l 2
Il secondo membro dell’uguaglianza è costituito da due addendi uguali ed è pertanto
uguale al doppio di uno di essi;quindi:
D2 =2 x l2
Estraiamo la radice quadrata di ciascun membro e,ricordiamo che la radice quadrata
di un prodotto indicato è uguale al prodotto delle radici quadrate dei singoli
fattori,possiamo scrivere:
D= 2xl2
Ma = l perché la radice quadrata del quadrato di un numero è uguale al numero
stesso
Otteniamo in definitiva d= 2xl
cioè
d=lx 2
Perché la misura della diagonale di
un quadrato si ottiene moltiplicando
per radice quadrata di 2 la misura
del suo lato???
• Poiché ogni triangolo rettangolo isoscele si può
considerare come la metà di un
quadrato,valgono le formule stabilite
precedentemente per il quadrato.