Indici di variabilità - Dipartimento di Scienze della Formazione

Indici di variabilità
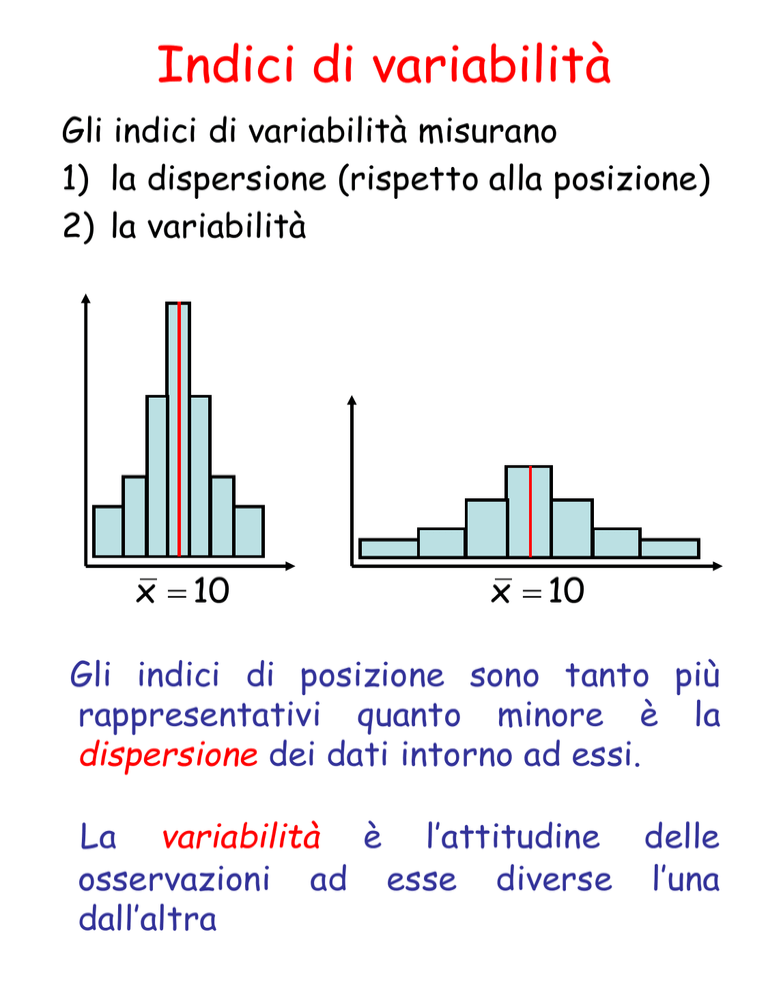
Gli indici di variabilità misurano
1) la dispersione (rispetto alla posizione)
2) la variabilità
x  10
x  10
Gli indici di posizione sono tanto più
rappresentativi quanto minore è la
dispersione dei dati intorno ad essi.
La variabilità è l’attitudine delle
osservazioni ad esse diverse l’una
dall’altra
Voti Master
Studente Matematica
A
25
B
23
C
25
B
25
E
28
F
28
G
26
H
25
I
26
L
22
M
26
N
22
O
20
P
27
Algebra
24
24
24
24
27
24
24
24
27
21
27
21
24
24
Probabilità Inferenza
28
24
24
25
30
27
27
23
26
28
26
24
26
28
25
26
27
25
25
21
23
26
20
20
25
24
30
25
La varianza
Dati n valori x1 , x2,
, xn con media x , la
la varianza è definita come segue
n
1
2
2
s    xi  x 
n i1
Essa indica qual è la concentrazione
delle osservazioni intorno alla media,
fornendo indicazioni sull’ordine di
grandezza degli scarti.
s2  x(2)  x 2
dove x(2)
1 n 2
  xi
n i1
Scarto quadratico medio
 s
2
Esempio 4.1 - Varianza
Dati:
(1, 2, 5, 6, 7, 9)
x 5
1. Media dei quadrati degli scarti
1
s  (1  5)2  (2  5)2  (5  5)2
6
 (6  5)2  (7  5)2  (9  5)2   7.67
2
2. Differenza fra la media dei
quadrati e il quadrato della media
1
x2  12  22  52  62  7 2  92   32.67
6
s2  32.67  52  7.67
Scarto
quadratico
medio
  7.67  2.77
Varianza
da distribuzione di frequenza
X assume
k valori
x1, x2, …, xk
con frequenze n1, n2, …, nk
1.
2.
k
1
2
2
s    xi  x  ni
n i1
s2  x(2)  x 2
1 k 2
dove x(2)   xi ni
n i1
Esempio 4.2 – Varianza Voti in algebra
Tabella 4.2 – Calcolo della varianza dei voti in Algebra.
2
2
xi
xi  x
ni
 xi  x 
 xi  x  ni
21
24
27
Totale
2
9
3
14
-3.21
-0.21
2.79
10.3041
0.0441
7.7841
k
20.6082
0.3969
23.3523
44.3574
x  x 
i1
2
i
ni
1 k
1
2
s    xi  x  ni  44.3574
n i1
14
 3.17
2
Scarto
quadratico
medio
  3.17  1.78
Esempio 4.2 – Varianza dei voti in
Probabilità
Tabella 4.3
quadrati dei voti
yi
ni
20
1
23
1
24
1
25
3
26
3
27
2
28
1
30
2
Totale
14
y(2)
– Media dei
in Probabilità.
yi2
yi2ni
400
400
529
529
576
576
625 1875
676 2028
729 1458
784
784
900 1800
9450
1 k 2
9450
  yi ni 
 675
n i1
14
s2  y(2)  y 2  675  25.862
 6.26
Scarto
quadratico   6.26  2.50
medio
k
2
y
 i ni
i1
Varianza da dati
raggruppati in classi
k classi
(x0 – x1), (x1 – x2),  , (xk-1 – xk)
con frequenze n1, n2,  , nk
e valori centrali x1 , x2 , … , xk
1.
s2
1 k
2
 xi  x  ni

n i1
s  x(2)  x
1 k 2
dove x(2)
xi ni

n i1
2.
2
2
Esempio 4.3 – varianza rendimenti
Tabella 4.4 – Calcolo della varianza per i rendimenti .
Classi
xi
ni
xi  x
- 1.0 |– 1.0
1.0 |– 2.0
2.0 |– 3.0
3.0 |– 4.0
4.0 |– 6.0
6.0 |– 8.0
8.0 |– 10.0
10.0 |– 12.0
Totale
0.0
1.5
2.5
3.5
5.0
7.0
9.0
11.0
9
23
24
8
9
3
3
1
80
-2.83
-1.33
-0.33
0.67
2.17
4.17
6.17
8.17
x  2.83
x
i
x
2
x
i
8.01
1.77
0.11
0.45
4.71
17.39
38.07
67.75
k
 x  ni
72.09
40.71
2.64
3.60
42.39
52.17
114.21
67.75
395.56
x  x  n
i1
2
i
i
k
1
1
2
2
s    xi  x  ni 
395.56  4.94
n i1
80
  4.94  2.22
2
Esempio 4.3 – varianza rendimenti
Tabella 4.5 – Calcolo della media dei quadrati
Classi
-1.0 |– 1.0
1.0 |– 2.0
2.0 |– 3.0
3.0 |– 4.0
4.0 |– 6.0
6.0 |– 8.0
8.0 |– 10.0
10.0 |– 12.0
Totale
2
xi
ni
xi
0.0
1.5
2.5
3.5
5.0
7.0
9.0
11.0
9
23
24
8
9
3
3
1
80
0.00
2.25
6.25
12.25
25.00
49.00
81.00
121.00
2
xi ni
0.00
51.75
150.00
98.00
225.00
147.00
243.00
121.00
1035.75
k
x  2.83
x(2)
s2
2
x
 i ni
i1
1 k 2
1035.75
  xi ni 
 12.95
n i1
80
x(2)  x 2  12.95  2.832  4.94
Coefficiente di variazione
Sia X una variabile statistica
 che assume valori positivi, X>0,
 con media x
 scarto quadratico medio  ,
il coefficiente di variazione è dato da
CV 

x
Il coefficiente di variazione non dipende
dall’unità di misura
Esempio – coefficiente di variazione
Tabella 4.6 – Tempo impiegato dagli operatori di un call center.
1.32
2.64
3.32
3.77
4.56
1.65
2.74
3.34
3.90
4.56
1.67
2.82
3.36
3.96
4.61
1.73
2.95
3.39
4.06
4.63
1.78
2.97
3.42
4.11
4.70
2.08
2.98
3.42
4.19
4.74
2.16
3.06
3.45
4.20
4.77
2.19
3.09
3.47
4.21
4.77
2.21
3.11
3.49
4.28
4.92
x  3.5
s2  1.02
1.02
CV 
 0.29
3.5
2.34
3.16
3.62
4.32
5.12
2.42
3.25
3.63
4.46
5.24
2.63
3.28
3.76
4.54
5.51
MAD
Median Absolute Deviation
o X:
x1, x2, … , xn
o med = median(X)
MAD  1.483 mediana  xi  med 
o Se la distribuzione è “normale” il
MAD approssima lo scarto
quadratico medio
o Non risente dei valori anomali
Esempio - MAD
Consumi pro-capite annui di cereali
med=72
xi
xi  med
xi  med
58
64
68
70
71
71
72
74
76
78
87
103
121
14
8
4
2
2
1
0
2
4
6
15
31
49
0
1
1
2
2
4
4
6
Scarti
ordinati
mediana
prof  med   7
med xi  med   4
MAD  1.483  4  5.932
  16.335
Differenza interquartile
 x(1), x(2), … , x(n)
 Quartili Q1 e Q3
DQ  Q3  Q1
Misura la variabilità della metà centrale
dei dati
Campo di variazione
xn   x1
Esempio – Differenza interquartile e
campo di variazione
Carne
( 55, 61, 62, 66, 68, 75, 85, 86, 88, 91, 97,
107, 152, 231, 299, 329 )
Sintesi
M
Q
E
87
67
55
129.5
329
QD  Q3  Q1  129.5  67  62.5
xn   x1  329  55  274
  83.91
Box-plot
Il box plot è un grafico utile per
rappresentare la distribuzione dei dati
Esso è costituito da
1. Una linea in corrispondenza della
mediana
2. Un rettangolo da Q1 a Q3 che indica
la variabilità della metà centrale dei
dati
3. Due segmenti (baffi) che si
estendono dai quartili ai valori
estremi
Esempio – Box-plot
Voti in matematica
( 20, 22, 22, 23, 25, 25, 25, 25, 26, 26,
26, 27, 28, 28 )
M
Q
E
25
23
20
26
28
Box-plot – Voti in matematica
28
26
24
22
20
Confronto fra Box-plot
Diversa
posizione
Diversa
variabilità
Diversa
asimmetria
Consumi di energia
5500
5000
4500
4000
Lunedi
Martedi Mercoledi Giovedi
Venerdi
Sabato Domenica
Box-plot dei consumi di energia nel Queensland
(Australia) nei diversi giorni della settimana, anno
2000.
Classificazione delle osservazioni
Obiettivo: identificare i dati anomali
Si definisce un intervallo di valori ritenuti
nella norma:
Recinto interno = (r1, r2)
r1  Q1  1.5  DQ,
r2  Q3  1.5  DQ
I valori al di fuori del recinto interno sono
definiti “osservazioni distanti”
Recinto esterno = (R1, R2)
R1  Q1  3  DQ,
R2  Q3  3  DQ
I valori al di fuori del recinto esterno
sono chiamati
“osservazioni molto distanti”
R1
Molto
distanti
distanti
r1
r2
R2
nella norma distanti Molto
distanti
Esempio – Classificazione delle
osservazioni
(-3, 10, 11, 13, 15, 17, 18, 19, 25, 48)
M
Q
E
n=10
DQ=8
r1  11  1.5  8  1,
16
11
-3
19
48
r2  19  1.5  8  31
r,r
1 2    1,31 
(10, 25)  valori adiacenti:
Massimo e minimo all’interno del recinto interno
R1  11  3  8  13,
R2  19  3  8  43
R1,R2    13, 43
 -3 osservazione distante
 48 osservazione molto distante
Esempio – Classificazione delle
osservazioni
(-3, 10, 11, 13, 15, 17, 18, 19, 25, 48)
n=10
DQ=8
r,r
1 2    1,31 
R1,R2    13, 43
f
out
F
far
-1
1
-13
-
M5.5
Q3
E
31
43
1
16
11
-3
Ad.: 10, 25
Out: -3
Far: 48
19
48
Box-plot con osservazioni anomale
o I baffi si estendono fino alle
osservazioni adiacenti
o Le osservazioni anomale sono
rappresentate all’esterno del boxplot con simboli diversi
50
Recinto esterno
osservazione
molto distante
40
Recinto interno
30
20
10
0
-10
osservazione
distante
Esempio – Box-plot consumi di carne
( 55, 61, 62, 66, 68, 75, 85, 86, 88, 91,
97, 107, 152, 231, 299, 329 )
M8.5
87
Q4.5 67
129.5
E
55
329
QD  62.5
r1  67  1.5  62.5  26.75,
r2  129.5  1.5  62.5  223.25
R1  67  3  62.5  120.5,
R2  129.5  3  62.5  317.00
f
-26.75
out
-
F
far
-120.5
-
223.25
2
317.0
1
Ad.: 55, 152
Out:
231(Paesi Bassi),
299(Irlanda)
Far:
329(Danimarca)
Box-Plot – Consumi di carne
f
-26.75
out
-
F
far
300
-120.5
-
223.25
2
317.0
1
Ad.: 55, 152
Out:
231(Paesi Bassi),
299(Irlanda)
Far:
329(Danimarca)
Danimarca
Irlanda
250
Paesi Bassi
200
150
100
50
Box-plot - Voti
30
28
E, I, M
26
24
22
N, L
N
20
Matematica
Algebra
Probabilità
N
Inferenza