Laboratorio di
fisica
Esercitazione pratica: Piano Inclinato
Confronto tra “P parallela teorica” e “P parallela sperimentale”
Classe IIIB Scientifico Tecnologico “E. Medi” Galatone
a.s. 2008/2009
Realizzato da: Leonardo Greco e Pasquale Carratta
Confronto tra “P parallela teorica” e “P
parallela sperimentale”
Cenni teorici
Apparecchiature e strumenti
Esercitazione pratica: Simulazione
Descrizione
Conclusioni
Fine della presentazione
Cenni teorici
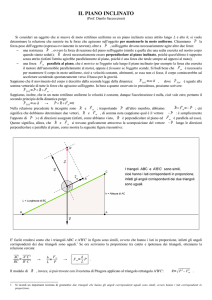
La forza peso del corpo (P) è un vettore che ha come componenti:
1. Forza peso parallela al piano inclinato
2. Forza peso perpendicolare al piano inclinato
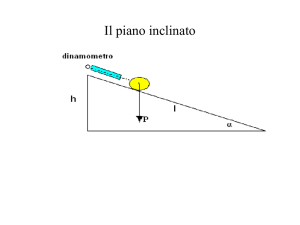
Apparecchiature e strumenti
Dinamometro
Corpo
Piano inclinato con goniometro
Dinamometro
Il dinamometro è uno
strumento per la
misurazione del peso. La
sua struttura è molto
semplice poiché è
costituito da una molla con
una scala graduata in
newton. Poiché secondo la
legge di Hooke, la
deformazione elastica di
una molla è proporzionale
alla forza applicata, una
misura dell'allungamento x
fornisce indirettamente
una misura della forza F.
Corpo
In fisica, un corpo è una porzione di
materia.
Si consideri che il corpo è dotato di massa
(inerziale, gravitazionale) e che di esso si
può determinare la posizione, la velocità e
in alcuni casi l'orientazione nello spazio, e
come queste cambiano sotto l'azione delle
forze ad esso applicate. Al concetto di
posizione si associa il concetto di volume.
Su quest'ultima proprietà si basa la
definizione aristotelica di corpo: "Corpo è
ciò che ha estensione in ogni direzione“.
In questa esercitazione il corpo che deve essere utilizzato deve avere le
seguenti proprietà:
•gancio per il dinamometro;
•scivolare sul piano.
Piano inclinato con goniometro
Il piano inclinato è uno dei primi
sistemi fisici ad essere stato
studiato da scienziati ellenistici e
poi da Galileo Galilei.
È la macchina più semplice: un piano
ben levigato, per far sì che
l'attrito sia trascurabile, che
forma con l'orizzontale un angolo.
Lungo tale piano si fa quindi
scivolare un corpo, generalmente
sferico, anch'esso ben levigato, e
quindi effettuando misurazioni a
vari angoli e con varie masse, si
riesce a determinare il valore
dell'accelerazione di gravità,
ovvero quella grandezza che
regola il moto dei corpi verso il
centro della Terra.
Galileo Galilei
Nasce, il 15 febbraio 1564, a Pisa da
nobile famiglia fiorentina.
Nel 1581 Galileo entra all'università di
Pisa, dove segue i corsi dei
maestri aristotelici, legge Platone
ed Aristotele, e soprattutto
approfondisce lo studio della
matematica.
È di quegli anni la prima scoperta: la
legge dell'isocronismo del moto
pendolare, compiuta, secondo il
tipico processo galileano,
osservando oscillare una lampada
nel duomo di Pisa. Nell'85 lascia
Pisa senza conseguire alcun titolo
accademico, e torna a Firenze.
Qui, approfondendo sempre più lo studio della geometria, in particolar modo
di Archimede, giunge sia alle fondamentali ricerche sul baricentro dei solidi.
Galileo Galilei
Altra importante scoperta
fatta da Galilei con gli
esperimenti sul piano
inclinato è la legge di
conservazione dell'energia:
notò infatti che il moto (in
particolare la velocità)
della sfera lungo il piano è
indipendente dalla massa
della sfera stessa. Questo
risultato è stato ripetuto
con l'esperimento della
caduta dei gravi, che ha
verificato come tutti i corpi
cadano con la stessa
velocità, laddove è
trascurabile la resistenza
opposta dal mezzo (l'aria).
Descrizione
Azzerando il dinamometro, lo si monta sul piano inclinato
assieme a corpo. Fissato un ipotetico angolo, si legge col
dinamometro la “P parallela sperimentale”.
La prova consiste nel confrontare la “P parallela sperimentale”
(quella letta dal dinamometro) con la “P parallela” calcolata
teoricamente tramite l’equazione:
= P * sen(angolo)
Conclusioni
Dalla costruzione di una tabella, si evince
che la “P parallela sperimentale”,
nell’ambito dell’errore, coincide con la “P
parallela teorica”.
Tabella
Tabella
Angolo
P parallela
teorica
(N)
P parallela
sperimentale
(N)
15°
0,26 ± 0,03
0,27 ± 0,01
20°
0,34 ± 0,03
0,35 ± 0,01
25°
0,42 ± 0,04
0,43 ± 0,01
30°
0,50 ± 0,05
0,50 ± 0,01